2005年～2006年度姜堰市溱潼中学高一年级第二学期
高一数学期末复习综合试题一
班级 姓名
一、选择题：
1．已知角
的终边经过点
，且
，则m的值是（ D ）
A、
B、
C、
D、
2．如果向量
与
共线且方向相反，则
=（ B ）
A、
B、
C、2
D、0
3．若不等式2x－3>4与不等式
的解集相同，则
= （ C ）
A、
B、
C、
D、
4．设等差数列{an}前n项和为Sn，则使S6=S7的一组值是（ C ）
A、
B、
C、
D、
5．为了得到
的图像，只需把
的图像上所有的点（ C ）
A、向左平移
个单位长度，再把所得各点的横坐标缩短到原来的
倍（纵坐标不变）
B、向右平移个单位长度，再把所得各点的横坐标缩短到原来的倍（纵坐标不变）
C、向左平移个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变）
D、向右平移个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变）
6．已知两点
、
，点P为坐标平面内的动点，满足
，则动点P（x，y）的轨迹方程为（ B ）
A、
B、
C、
D、
7．设a、b、c是互不相等的正数，则下列等式中不恒成立的是（ C ）
A、
B、
C、
D、
8．等比数列前3项依次为：1，a，
，则实数a的值是（ D ）
A、
B、
C、
D、或
二、填空题：
9．函数
的定义域为 
．
10．在△ABC中，已知BC＝12，∠A＝60°，∠B＝45°，则AC＝ 
．
11．设变量x、y满足约束条件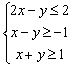
，则
的最大值为 18 ．
12．
＝ 2 ．
13．不等式
的解集为
．
 |
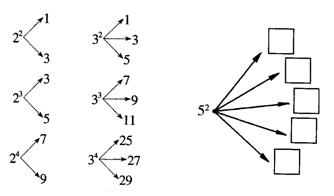14．对大于或等于2的自然数m的n次幂进行如下方式的“分裂”，
仿此，52“分裂”中最大的数是 9 ，若m3的“分裂”中最小的数是211，则m的值为 105 ．
三、解答题：
15．若a为实数，设函数
；令t＝
，求t的取值范围，并把f(x)表示为t的函数m(t)．
解：由
有意义可知：
；
可设：
，从而
；
∴ 
故：t的取值范围
；
由t＝可知：
故：
．
16．在△ABC中A、B、C所对的边的长分别为a、b、c，已知向量
，
，满足
，b+c=
a；（1）求A的大小；（2）求
的值．
解：（1）由
，得
………………2分
即
；
∴
或
………………4分
∵A是△ABC的内角，∴ 舍去
∴
………………6分
（2）∵
；∴由正弦定理，
………………8分
∵
；
∴
………………10分
∴
即
……………12分
17．已知数列
、
满足：
为常数），且
，其中
…
（1）若{an}是等比数列，试求数列{bn}的前n项和
的表达式；
（2）当{bn}是等比数列时，甲同学说：{an}一定是等比数列；乙同学说：{an}一定不是等比数列；你认为他们的说法是否正确？为什么？
解：（1）∵{an}是等比数列a1=1，a2=a；
∴ a≠0，an=an－1；
又∵
；
∴
；
即
是以a为首项，a2为公比的等比数列；∴ 
；
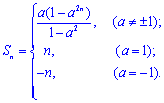（2）甲、乙两个同学的说法都不正确，理由如下：
{an}可能是等比数列，也可能不是等比数列，举例说明如下：
设{bn}的公比为q；
①取a=q=1时，an=1(n∈N)，此时bn=anan+1=1，{an}、{bn}都是等比数列.
②取a=2，q=1时，
所以{bn}是等比数列，而{an}不是等比数列．
18．设数列
、
、
满足：
，
（n=1,2,3,…），
证明：（1）当数列为等差数列时，数列也为等差数列且
（n=1,2,3,…）；
（2）当数列为等差数列且（n=1,2,3,…）时，数列也为等差数列．
证：（1）设数列
是公差为
的等差数列，则：
=
=
=0，
∴
（n=1,2,3,…）成立；
又
=6（常数）（n=1,2,3,…）
∴数列
为等差数列。
（2）设数列是公差为
的等差数列，且（n=1,2,3,…），
∵
……①
∴
……②
①－②得：
=
；
∵
；
∴
……③
从而有：
……④
④－③得：
……⑤
∵
，
，
；
∴由⑤得：
（n=1,2,3,…），
由此，不妨设
（n=1,2,3,…），则
（常数）
故：
……⑥
从而：
……⑦
⑦－⑥得：
，
故；
（常数）（n=1,2,3,…），
∴数列为等差数列．