三角函数单元测验试题
一、选择题:(本大题共10小题,每题3分,共计30分,在每题给出的四个选项中,只有一个是正确的)
1、与![]() 终边相同的角可以表示为
终边相同的角可以表示为![]() ( )
( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
2、已知![]() 是第三象限的角,且
是第三象限的角,且![]() ,那么
,那么![]() 为 ( )
为 ( )
(A)第一象限的角 (B)第二象限的角 (C)第三象限的角 (D)第四象限的角 3、若![]() ,则
,则![]() 的值是
( )
的值是
( )
(A)1 (B)0 (C)![]() 1 (D)不能确定
1 (D)不能确定
4、下列四个命题中,正确的是 ( )
(A)sin2<sin3<sin4 (B)sin4<sin2<sin3
(C)sin3<sin4<sin2 (D)sin4<sin3<sin2
5、![]() 的值是
( )
的值是
( )
(A)4 (B)1 (C)![]() (D)
(D)![]()
6、满足sin4xcos5x![]() cos4xsin5x的x的一个值是
( )
cos4xsin5x的x的一个值是
( )
(A)10![]() (B)20
(B)20![]() (C)50
(C)50![]() (D)70
(D)70![]()
7、要得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象( )
的图象( )
(A)向右平移个![]() 单位 (B)向左平移个
单位 (B)向左平移个![]() 单位
单位
(C)向右平移个![]() 单位 (D)向左平移个
单位 (D)向左平移个![]() 单位
单位
8、若![]() ,且
,且![]() 为第二象限的角,则
为第二象限的角,则![]() 的值为
( )
的值为
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)以上全不对
(D)以上全不对
9、设![]() +4,其中a、b、
+4,其中a、b、![]() 、
、![]() 均为非零的常数,若
均为非零的常数,若![]() ,则
,则![]() 的值为
( )
的值为
( )
(A)1 (B)3 (C)5 (D)不确定
10、若![]() 是三角形的内角,且函数
是三角形的内角,且函数![]() 对于任意实数x均取正值,那么
对于任意实数x均取正值,那么![]() 的取值范围是
( )
的取值范围是
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、填空题:(本大题共5小题,每题4分,共20分)
11、若![]() 、
、![]() 为锐角,且
为锐角,且![]() ,
,![]() ,则
,则![]() 等于 .
等于 .
12、函数![]() 为增函数的区间是 .
为增函数的区间是 .
13、已知函数![]() 是偶函数,则
是偶函数,则![]() 的值为 .
的值为 .
14、函数![]() 的值域是
.
的值域是
.
15、若![]() ,且
,且![]() ,则
,则![]() .
.
三、解答题(本题满分共50分)
16、(本小题满分10分)设![]() ,
,![]() 是方程
是方程![]() 的两根,求m与
的两根,求m与![]() 之值.
之值.
17、(本小题满分10分)已知![]() ,且450
,且450![]() <
<![]() <540
<540![]() ,求
,求![]() 之值.
之值.
18、(本小题满分12分)已知函数![]() .
.
(1)求![]() 的最小正周期; (2)求
的最小正周期; (2)求![]() 的最小值及取最小值时相应的x的值;
的最小值及取最小值时相应的x的值;
(3)函数![]() 在那些区间上是增函数?
在那些区间上是增函数?
19、(本小题满分18分)某港口水的深度y(米)是时间t(0![]() t
t![]() 24,单位:时)的函数,记作y=f(t),下面是某日水深的数据:
24,单位:时)的函数,记作y=f(t),下面是某日水深的数据:
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 10.1 | 13.0 | 9.9 | 7.0 | 9.9 | 13.0 | 10.1 | 7.0 | 10.0 |
经长期观察,y=f(t)的曲线可以近似地看成函数![]() 的图象.
的图象.
(1)试根据以上数据,画出函数![]() 的草图,并求其近似表达式;
的草图,并求其近似表达式;
(2)试说明![]() 的图象可由
的图象可由![]() 的图象经过怎样的变换得到;
的图象经过怎样的变换得到;
(3)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).某船吃水深度(船底离水面的距离)为6.5米.如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长时间(忽略进出港所需的时间).
参考答案:
一、选择题:1、C 2、B 3、A 4、D 5、C 6、C 7、A 8、A 9、B
10、A
二、填空题:11、![]() .
.
12、![]() 13、
13、![]()
14、![]() 15、
15、![]()
三、解答题
16、解:由已知得
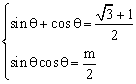
又![]()
∴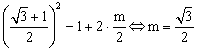
![]()
17、解:![]() ,又
,又![]() 在第二象限,故
在第二象限,故![]()
所以![]() ,
,![]()
![]()
18、解:(1)![]()
![]()
![]() 的最小正周期为
的最小正周期为![]()
(2)![]() ,即
,即![]() 时,
时,![]() 取最小值
取最小值![]() .
.
(3)由![]() 得,
得,![]()
所以![]() 在每一个区间
在每一个区间![]() 上是增函数.
上是增函数.
19、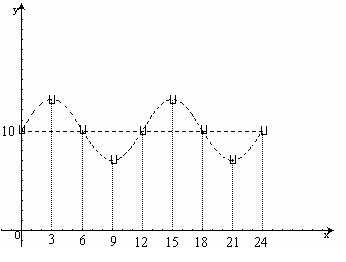 解:(1)
解:(1)![]()
(2)![]() 的图象上各点的横坐标伸长为原来的
的图象上各点的横坐标伸长为原来的![]() 倍(纵坐标不变)得到
倍(纵坐标不变)得到![]() 的图象,再将
的图象,再将![]() 的图象上各点的纵坐标变为原来的3倍(横坐标不变)得到
的图象上各点的纵坐标变为原来的3倍(横坐标不变)得到![]() 的图象,然后将
的图象,然后将![]() 的图象向上平移10个单位得到函数
的图象向上平移10个单位得到函数![]() 的图象;
的图象;
(3)由题意,该船进出港时,水深应不小于5+6.5=11.5(米)
∴![]() ,即
,即![]()
解得,![]() ,即
,即
![]()
在同一天内,取k=0或1,∴1![]() t
t![]() 5,或13
5,或13![]() t
t![]() 17
17
∴该船最早能在凌晨1时进港,下午17时出港,在港口内最多停留16个小时.