三角函数期末精讲精练
三角函数精讲
一、基本概念、定义：
1. 角的概念推广后，包括 、 、 ，与α终边相同的角表示为 。
终边角： x轴上 y轴上
第一象限 第二象限
第二四象限 直线y＝x上
2. 弧度制：把 叫1弧度的角。
公式：α＝—
换算：180°＝ 弧度；
1弧度＝ 度； 1°＝ 弧度
扇形： 弧长L＝ ＝
，面积S＝
＝
3. 任意角的三角函数：
①定义：角α终边上任意一点P(x，y)，则r＝ ，六个三角函数的定义依次是 、
、 、 、 、 。
②三角函数线：角的终边与单位圆交于点P，过点P作 轴的垂线，垂足为M，则
。过点A(1,0)作 ，交 于点T，则 。
③同角三角函数关系式：
平方关系： 商数关系： 倒数关系：
④诱导公式：
| 角x | Sinx | Cosx | Tanx | Sin( Tan( 能推导： 口诀：函数名变反，符号看象限。 |
| π—α | ||||
| π＋α | ||||
| —α | ||||
| 2π-α | ||||
| 2kπ+α | ||||
| 口诀 | ||||
－α)＝ cos(
＋α；二、基本三角公式：（1～2要求能熟练运用：顺用、逆用、变形用，3～6要求能证明，不记忆）
1．和、差角公式
2．二倍角公式
＝
＝
倍角公式变形：降幂公式
3．半角公式(书P45～46)
, 
, 
4．万能公式：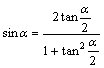 
；
；
．
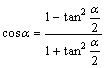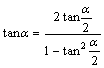5．积化和差公式(书P46～47)
； 
；
； 
．
6．和差化积公式(书P46～47)
；
；
；
．
应用公式解题的基本题型：化简、求值、证明
基本技巧：
①1的妙用：1＝ ＝ ＝
②变角： (x+y)＋(x－y)＝ (x+y)＋(x－y)＝ α＝ ＝ ＝ 等
③变名：切化弦；弦化切
④化一：a sinx＋b cosx＝
三、三角函数性质
| 函数 | 正弦函数y＝sinx | 余弦函数y=cosx | 正切函数y＝tanx |
| 图像 |
|
|
|
| 定义域 | |||
| 值域 | 值域： 当x＝ 时y最小； 当x＝ 时y最大； | 值域： 当x＝ 时y最小； 当x＝ 时y最大； | 值域： |
| 周期/奇偶 | 周期T＝ 奇偶性： | 周期T＝ 奇偶性： | 周期T＝ 奇偶性： |
| 单调性 | 增： 减： | 增： 减： | 增区间： |
| 对称中心 | |||
| 对称轴 |
四、y＝Asin(ωx＋ψ)的图像和性质：
1、 作图：五点法，依次取ωx＋ψ＝
2、 周期T＝
3、 单调区间：A
ω>0时，增区间：解不等式
≤ωx＋ψ≤
减区间：解不等式 ≤ωx＋ψ≤
Aω<0时，增区间：解不等式
≤ωx＋ψ≤
减区间：解不等式 ≤ωx＋ψ≤
4、最大值：A>0时，当ωx＋ψ＝ 时，y取最大值A。
最小值：A>0时，当ωx＋ψ＝ 时，y取最小值－A。
5、概念：振幅 ；周期T＝ ；频率f＝ ；初相 ；相位 。
6、三角变换： (A>0，ω>0)
将y＝sinx的图像—————————>y＝sin(x＋ψ) ——————————>y＝sin(ωx＋ψ)
——————————>y＝Asin(ωx＋ψ)
或者： 将y＝sinx的图像—————————>y＝sin(ωx) —————————>y＝sin(ωx＋ψ)
——————————>y＝Asin(ωx＋ψ)
7、联系： y＝tan((ωx＋ψ) (ω>0)的周期是T＝ ，单调 区间是解不等式 。
五、反三角定义：
1.在闭区间 上，符合条件sinx＝a (-1≤a≤1)的角x叫a的反正弦，记作：x＝
在闭区间 上，符合条件cosx＝a (-1≤a≤1)的角x叫a的反余弦，记作：x＝
在开区间 上，符合条件tanx＝a的角x叫a的反正切，记作：x＝
2.反三角的三角函数、三角函数的反三角：
例：sin(arcsinx)＝
，其中x∈[-1,1]；arcsin（sinx）＝ ，其中x∈[－
，]；
六、数学思想方法： 数形结合思想，例如：解三角不等式可以用 、或 ；
整体思想，例如：研究函数y＝Asin(ωx＋ψ)的图像和性质可以把 看成整体
三角函数精练
A
⒈ 已知α是钝角，那么 是 （ ）
A．第一象限角 B．第二象限角
C．第一与第二象限角 D．不小于直角的正角
2． 角α的终边过点P（－4k，3k）(k＜0}，则cosα的值是 （ ）
A． B． C．－ D．－
3．已知点P(sinα－cosα，tanα)在第一象限，则在［0，2π］内，α的取值范围是 ( )
A．( ， )∪(π， ) B．( ， )∪(π， )
C．( ， )∪(，) D．( ， )∪( ，π)
4．若sinx= － ，cosx = ，则角2x的终边位置在 ( )
A．第一象限 B．第二象限 C．第三象限 D．第四象限
5．若4π＜α＜6π，且α与－ 终边相同，则α= ．
6． 角α终边在第三象限，则角2α终边在 象限．
7．已知｜tanx｜=－tanx，则角x的集合为 ．
8．如果θ是第三象限角，则cos(sinθ)·sin(sinθ)的符号为什么？
9．已知扇形AOB的周长是6cm，该扇形中心角是1弧度，求该扇形面积．
B
1．sin600°的值是 （ ）
A． B．－ C． D．－
2． sin(+α)sin（－α）的化简结果为 （ ）
A．cos2α B．cos2α C．sin2α D． sin2α
3．已知sinx+cosx=，x∈［0，π］，则tanx的值是 （ ）
A．－ B．－ C．± D．－或－
4．已知tanα=－，则 = ．
5． 的值为 ．
6．证明 =．
7．已知=－5，求3cos2θ+4sin2θ的值．
8．已知锐角α、β、γ满足sinα+sinγ=sinβ，cosα－cosγ=cosβ，求α－β的值．
C.
1．已知0＜α＜＜β＜π，sinα=，cos(α+β)=－，则sinβ等于 （ ）
A．0 B．0或 C． D．0或－
2． 的值等于 （ ）
A．2+ B． C．2－ D．
3． △ABC中，3sinA+4cosB=6，4sinB+3cosA=1，则∠C的大小为 （ ）
A． B． C． 或 D． 或
4．若α是锐角，且sin(α－)= ，则cosα的值是 ．
5．coscoscos = ．
6．已知tanθ=，tanφ=，且θ、φ都是锐角．求证：θ+φ=45°．
7．已知cos(α－β)=－，cos(α+β)= ，且（α－β）∈（，π），α+β∈（，2π），求cos2α、cos2β的值．
8． 已知sin(α+β)= ，且sin(π+α－β)= ，求．
D
1．cos75°+cos15°的值等于 （ ）
A． B － C． － D．
2．a=（sin17°+cos17°），b=2cos213°－1，c= ，则 （ ）
A．c＜a＜b B． b＜c＜a C． a＜b＜c D． b＜a＜c
3．化简= ．
4．化简sin(2α+β)－2sinαcos(α+β)= ．
5．在△ABC中，已知A、B、C成等差数列，则tan+tan+tantan的值为 ．
6．化简sin2A+sin2B+2sinAsinBcos(A+B)．
7 化简sin50°(1+tan10°)．
8 已知sin(α+β)=1，求证：sin(2α+β)+sin(2α+3β)=0．
E
1．函数y=lg(2cosx－1)的定义域为 （ ）
A．{x｜－＜x＜} B．{x｜－＜x＜｝
C．{x｜2kπ－＜x＜2kπ+，k∈Z} D．{x｜2kπ－＜x＜2kπ+，k∈Z}
2．如果α、β∈（，π），且tanα＜cotβ，那么必有 （ ）
A．α＜β B． β＜α C． α+β＜ D． α+β＞
3．若f(x)sinx是周期为π的奇函数，则f(x)可以是 （ ）
A．sinx B． cosx C． sin2x D． cos2x
4．下列命题中正确的是 （ ）
A．若α、β是第一象限角，且α＞β，且sinα＞sinβ
B．函数y=sinxcotx的单调递增区间是（2kπ－，2kπ+），k∈Z
C．函数y= 的最小正周期是2π
D．函数y=sinxcos2φ－cosxsin2φ的图象关于y轴对称，则φ=＋，k∈Z
5．函数y=sin+cos在（－2π，2π）内的递增区间是 ．
6．y=sin6x+cos6x的周期为 ．
7．比较下列函数值的大小：（1）sin2，sin3，sin4； (2)cos2θ，sin2θ，tan2θ（＜θ＜）．
8．设f(x)=sin(x+) (k≠0) ．
(1)写出f(x)的最大值M，最小值m，以及最小正周期T；
（2）试求最小的正整数k，使得当自变量x在任意两个整数间（包括整数本身）变化时，函数f(x)至少有一个M与m．
F.
1．函数y= sin(2x+θ)的图象关于y轴对称的充要条件是 （ ）
A．θ=2kπ+ B．θ=kπ+ C．θ=2kπ+π D．θ=kπ+π(k∈Z)
2．先将函数y=sin2x的图象向右平移个单位长度，再将所得图象作关于y轴的对称变换，则所得函数图象对应的解析式为 （ ）
A．y=sin(－2x+ ) B．y=sin(－2x－)
C．y=sin(－2x+ ) D． y=sin(－2x－)
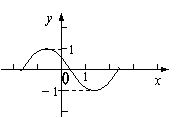
3．右图是周期为2π的三角函数y=f(x)的图象，
那么f(x)可以写成 （ ）
A．sin(1+x) B． sin(－1－x)
C．sin(x－1) D． sin(1－x)
4．y=tan(x－)在一个周期内的图象是 （ ）
 | |||||
 | |||||
 |
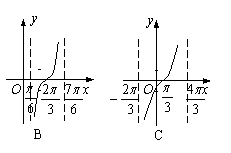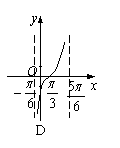5．已知函数y=2cosx(0≤x≤2π)的图象与直线y=2围成一个封闭的平面图形，则该封闭图形面积是 ．
6．将y=sin(3x－ )的图象向（左、右） 平移 个单位可得y=sin(3x+）的图像．
7．已知函数y=Asin(ωx+φ)，在同一个周期内，当x=时取得最大值，当x=时取得最小值－ ，若A＞0，ω＞0，｜φ｜＜，求该函数的解析表达式．
8．已知函数y=sinx+cosx，x∈R． (1)当y取得最大值时，求自变量x的取值集合；
（2）该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到？
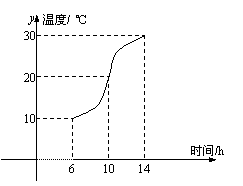
9．如图：某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b．
（1）求这段时间的最大温差；
（2）写出这段曲线的函数解析式．
G
1．函数y= 的最大值是 （ ）
A． －1 B． ＋1 C． 1－ D． －1－
2．若2α+β=π，则y=cosβ－6sinα的最大值和最小值分别为 （ ）
A．7，5 B． 7，－ C． 5，－ D． 7，－5
3．当0≤x≤时，函数f(x)= 的 （ ）
A．最大值为2，最小值为 B．最大值为2，最小值为0
C．最大值为2，最小值不存在 D．最大值不存在，最小值为0
4．已知关于x的方程cos2x－sinx+a=0，若0＜x＜时方程有解，则a的取值范围是（ ）
A．［－1，1］ B．（－1，1） C．［－1，0］ D．（－∞，－）
5．要使sinα－cosα= 有意义，则m的取值范围是 ．
6．若f(x)=2sinωx(0＜ω＜1），在区间［0，］上的最大值为，则ω= ．
7．y=sinxcosx+sinx+cosx，求x∈［0， ］时函数y的最大值．
8．已知函数f(x)=－sin2x－asinx+b+1的最大值为0，最小值为－4，若实数a＞0，求a，b的值．
9．已知函数f(x)=2cos2x+sin2x+a，若x∈［0，］，且｜f(x)｜＜2，求a的取值范围．
H
1．△ABC中，tanA+tanB+=tanAtanB，sinAcosA=，则该三角形是 （ ）
A．等边三角形 B．钝角三角形
C．直角三角形 D．等边三角形或直角三角形
2．在△ABC中，已知（b+c）∶(c+a)∶(a+b)=4∶5∶6，则此三角形的最大内角为 （ ）
A．120° B．150° C．60° D．90°
3．若A、B是锐角△ABC的两个内角，则点P（cosB－sinA，sinB－cosA）在 （ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
4．在△ABC中，若sinA∶sinB∶sinC=5∶12∶13，则cosA= ．
5．在△ABC中，3sinA+4cosB=6，4sinB+3cosA=1，则∠C的大小为 ．
6．已知a、b、c是△ABC中∠A、∠B、∠C的对边，S是△ABC的面积，若a=4，b=5，s=5，求c的长度．
7．在△ABC中，sin2A－sin2B+sin2C=sinAsinC，试求角B的大小．
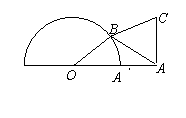8．半圆O的直径为2，A为直径延长线上一点，且OA=2，
B为半圆上任意一点，以AB为边向外作等边△ABC，问B
点在什么位置时，四边形OACB的面积最大，并求出这个最
大面积．
三角函数答案
A1． A 2． B 3． B 4． D 5． 6．一、二
7．{2kπ+ ＜x＜2kπ+π或2kπ+＜x＜2kπ+2π ，k∈Z＝ 8．负 9． 2cm2．
B1． D 2． B 3． B 4． 5． 1 6． 略 7． 8．－
C1． C 2． C 3． A 4． 5． 6．略
7． cos2α=－，cos2β=－1 8．
D1． A 2． A 3． tan θ 4． sinβ 5． 6． sin2（A＋B）．
7. 1 8 .略．
E1． C 2． C 3． B 4． D 5． [－ , π) 6．
7．（1）sin4 ＜sin3＜ sin2 （2）cos2θ＜sin2θ＜tan2θ
8．（1）M=1，m=－1，T= = （k≠0）． （2）k=32．
F1． B 2． D 3． D 4． A 5． 4 π 6．左，
7． y= sin(3x+) 8．（1）{x｜x=+2kπ，k∈Z｝； （2）将y=sinx的图象向左平移，得到函数y=sin(x+）的图象，再将所得图象上各点横坐标不变，纵坐标伸长到原来的2倍，得到函数y=2sin(x+）的图象．
9．（1）最大温差20℃； （2）y=10sin(x+）＋20，x∈[6，14]．
G1． B 2． D 3． A 4． A 5． －1≤m≤ 6．
7．+ 8．a=2, b=－2 9．－2＜a＜－1
H1． A 2． A 3． B 4． 5． 6． 或 7．
8． 设∠AOB=θ，θ= 时，S最大值 =2+