立体几何辅导练习三
一．概念复习：1。右手空间直角坐标系.2.空间向量的坐标运算.3.证明向量的垂直与平行.4.平面的法向量及求法向量的方法,求单位向量.5.线面角与二面角及它们的范围.6.如何求解线面与二面角的问题.7.等差数列与等比数列及求和公式.
二.例题: A A C C X<-2,C
8.设等比数列{an}前n项和为Sn ，若S3+S6=2S9，求数列的公比q。
红手册P207例2 答：
方法：基本元素法。
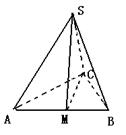9.在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=
,M为AB的中点.(1)证明:AC⊥SB;(2).求二面角S-CM-A的大小;(3)求点B到平面SCM的距离.
答 (1).略.
(2).
(3).
三.训练题:
8．在等比数列
中，
，
，那么
等于（ D ）
（A）27 （B）-27
（C）81或-36 （D）27或-27
9．已知等差数列的前n项和为
，若
等于（ D ）
A．18 B．36 C．54 D．72
12、已知等差数列
的公差
，首项 
，设为它的前 
项和 ，若数列 
的最大项为
，则 
=_______________________________.
 |
16．有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数与第四个数的和是16,第二个数与第三个数的和是12.求这四个数.
本小题考查等差数列、等比数列的概念和运用方程（组）解决问题的能力.
解法一:
①
由②式得 d=12-2a. ③
整理得 a2-13a+36=0
解得 a1=4,a2=9. 代入③式得 d1=4,d2=-6从而得所求四个数为0,4,8,16或15,9,3,1.
解法二:设四个数依次为x,y,12-y,16-x ①
由①式得 x=3y-12③.
将③式代入②式得 y(16-3y+12)=(12-y)2, 整理得 y2-13y+36=0
解得 y1=4,y2=9. 代入③式得 x1=0,x2=15.
从而得所求四个数为0,4,8,16或15,9,3,1.
.17．（本小题满分14分）
已知函数f(x)是定义在R上的偶函数，当x≥0时，
（I）求当x<0时，f(x)的解析式；
（Ⅱ）试确定函数y=f(x)（x≥0）的单调区间，并证明你的结论；
（Ⅲ）若
，且
证明：
。
解：（I）若x<0则-x>0，
∵f(x)是偶函数，∴
（Ⅱ）设
，
是区间
上的任意两个实数，且
，
则
当
时
，
而
及
∴
即f(x)在[0，1]上为减函数
同理，当
时，
，即f(x)在
上为增函数
（Ⅲ）∵f(x)在是增函数，由x≥2得
又
，-7x<0∴
，∴
∵，∴
且
即
∴
∴
答案 (1-10)B B B DD D D D D ①④ (11) 
或
(12).a1=15.(13).(2).30°. (14).略. (15) 
(2).