高一《数学》（上）综合练习六
一、选择题(本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的)
1、命题“2001≤2008” （ ）
A．使用了逻辑联结词“或” B．使用了逻辑联结词“且”
C．使用了逻辑联结词“非” D．是假命题
2、若集合S={x∈Zx－1<4},集合A={x∈N2 x≤16}集合B={ xx=2},则(CSA)∩(CSB)是
（ ）
A．{－2,－1,0,1,2,3,4} B．{－1} C．{－2,－1,0,1,3,4} D．{0,－1}
3、已知集合A={a,b,c},集合B={0,1}.映射f：A→B 满足f（a）．f(b)．=f(c).那么这样的 映射f：A→B有( )个.
A．0 B．2 C．3 D．4
4、条件p：x2≥－x,条件q：x=x,则p是q的 （ ）
A．必要不充分条件 B．充分不必要条件
C．充要条件 D．既不充分也不必要条件
5、在各项均为正数的等比数列{an}中,若a5a6=9,则log3a1+log3a2+…+log3a10的值为 （ ）
A．10 B．12 C．8 D．2+log 35
6．当
时，函数
的值有正值也有负值，则实数a的取值范围是（ ）
A 
B 
C 或
D 
7、已知函数f(x)＝－x－x3，x1，x2，x3∈R，且x1+x2＞0，x2＋x3＞0，x3＋x1＞0，则f(x1) ＋f(x2)＋f(x3)的值 （ ）
A．一定大于零 B．一定小于零 C．一定等于零 D．正负都有可能
8、对任意a∈[－1，1]，函数f(x)＝x2＋(a－4)·x＋4－2a的值总大于0，则x的取值范围是：
（ ）
A．{x1＜x＜3} B．{xx＜1或x＞3}
C．{x1＜x＜2} D．{xx＜1或x＞2}
9、某厂2000年12月份产值计划为当年1月份产值的n倍,则该厂2000年度产值的月 平均增长率为 （ ）
A．
B．
C．
－1
D．－1
10、根据市场调查结果,预测某种家用商品从年初开始的n个月内累积的需求量S n(万件)近似地满足Sn=
(21n－n2－5)(n=1,2,3…),按此预测,在本年度内,需求
量超过1.5万件的月份是 （ ）
A． 5月、6月 B．6月、7月 C．7月、8月 D．8月、9月
11、已知数列{a n}的前n项的和S n= n2－4n+1,则a 1+a2+……+a 10的值为 （ ）
A．56 B．61 C．65 D．67
12、将数列{3 n－1}按“第n组有n个数”的规则分组如下：1、,(3,9)(27,81,243),……则第100组中的第一个数是 （ ）
A．3 4950 B．3 5000 C．3 5010 D．35050
二、填空题(本大题共4小题，每小题4分，共16分，请将答案直接填在题中的横线上)
13、若函数f(x)=
alg(x+
)－x2,其中a为实常数,己知f(2)=5,那么f(－2)的值为___
.
14、某房地产公司要在荒地ABCDE上划出一块长方形地面(不改变方位，如图)建造一幢十层楼公寓.通过精心设计可使公寓占地面积最大，其最大值是______ .
|
15、设数列{a n}是首项为1的正项数列,且满足
(n=1,2,3…),则它的通项公式a n
= ______
.
16、已知等差数列{a n}的前n项的和S n=An 2－n,等比数列{b n}的前n项的和为T n= B(3n －1),n=1,2,3…又已知a 2－2=b 2, a 3－2 = b3,那么满足a n <b n的最小正整数n=____.
三、解答题（本大题共6小题，共74分。解答应写出必要的文字说明、证明过程或演算步骤）
17、（本小题12分）若A={xx2－3x+2=0}, B={xx2－ax+a－1=0}C={xx2－mx+1=0},且A∪B=A,A∩C=C,求a.
18、（本小题12分）己知f(x)=(
)2(x>1)
①求函数的反函数f－1(x)
②用单调性的定义证明：f －1(x)在定义域上为增函数
③若(1－
) f －1(x)>m(m－ )对在[
]上的每一个x的值恒成立,求实数m的取
值范围.
19、（本小题12分）设二次函数f(x)＝ax2＋bx＋c(a＞0，且 bc≠0)。
①若 f(0)＝ f(1)＝ f(－1)＝1，试求f(x)的解析式，并求f(x)的最小值；
②若f(x)的对称轴的方程是 x＝1，且f(x)的图象在x轴上截得的弦长不小于2，试分别判断b、c的符号。
20、（本小题12分）已知二次函数f(x)=x2 +2(10－3n)x+9n2－61n+100,其中n∈N*.
①设函数y=f(x)的图象的顶点的横坐标构成数列{a n},求证：数列{a n}为等差数列；
②设函数y=f(x)的图象的顶点到y轴的距离构成数列{d n},求数列{d n}前n项 的和S n .
21、（本小题12分）某企业经过调整后，第一年的资金增长率为300%,以后每年的资金的增长率都是前一年的
.
①经过4年后，企业的资金是原来资金的多少倍？
②如果由于某种原因,每年损失资金的5%,那么经过多少年后企业的资金开始 下降.
22、（本小题14分）已知数列{a n
}满足a 1
=2a, a n =2a－
(n≥2),其中a是不为零的常数,令bn=
①求证数列{b n }是等差数列；
②求数列{a n}的通项公式.
综合练习六参考答案
一、选择题：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A | B | D | A | A | D | B | B | D | C | D | A |
二、填空题：
（13）－13 （14）6017m2 （15）
（16）5
三、解答题：
（17）A={1，2}，B={x（x－1）[x－（a－1）]=0又
若B={1}，则a=2，若B={1，2}则a=3 又
，
若1∈C，则m=2此时，
，此时，
或3，
.
（18）①
②略③由题意：
即
对于一切
的x值恒成立，显然1+m≠0即
，则
恒成立.由一次函数的单调性可解得：
（19）①由a+b+c=a－b+c=c=1得：(a+b+c)2=(a－b+c)2即4(a+c)b=0 ∵b≠0 ∴a＝－c
又
此时
. 从而
有最小值
②
的图象的对称轴为x=1，
，即b=－2a，
设
的二根是x1、x2则函数
的图象与x轴的两个交点是（x1，0），（x2，0）且
，则满足弦长不小于2的充要条件是：
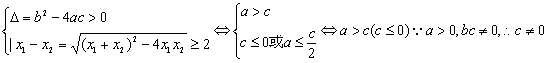
故c＜0.
（20）解：①顶点横坐标为
为等差数列.
②由题意，
当
（21）解：①设企业原有资金为a，调整后第n年资金为an（n=1，2，3……），则a1=a（1+300%）=4a，
经过4年后，企业资金是原来资金的
倍.
②若每年损失资金的5%，则第n年与第n－1年的产量关系为：
.经过4年后，从第5年起企业资金开始下降.
（22）① 
②