高一《数学》（上）综合练习四

高一《数学》（上）综合练习四  

一、选择题(本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的)

1.的值为

A.　　　 　　 　　　　　B. 　　　　　　 C. 　　　　　　D.

2.函数y=2-的值域为

A. [-2,2]　　　　　　　 B. [1,2]　　　　　  C. [0,2]　　　　　  D. [-，]

3.若不等式ax+bx+2＞0，的解集为（-，），则a+b的值为

A.10　　　　　　　　  B. [1,2]　　　　　  C. 14　　　　　　  D.-14

4.对于xR，f(x)满足，并且在（-∞,0）上是增函数，若x＜0，x＞0且│x│＜│x₁│＜│x₂│,则

A.f(-x₁)＞f(-x₂)　　　　  B.f(-x₁)＜f(-x₂)

C. f(-x₁)、f(-x₂)的大小由x₁、x₂的具体取值而定

D. f(-x₁)、f(-x₂)有相等的可能

5.已知等比数列的公比为q=-,则等于

A.-　　　　　　 B.-3　　　　　　 C.　　　　　  D.3

6.条件P：│x│=x，条件Q：x²≥-x,则P是Q的

A.充分不必要条件　　　　　　 B.必要不充分条件

C.充要条件　　　　　　　　　 D.既不充分也不必要条件

7.在等差数列｛a_n｝中，若a₃+a₄+a₅+a₆+a₇=450，则a₂+a₈等于

A.45　　　　　　 B.75　　　　　　 C.180　　　　   D.3008.集合M=｛x│logx≥0｝，N=｛y│y=｝，则M与N的系是

A.M N　　　　  B. N M　　　　C.M=N　　　　  D. MN=

9.已知函数f(x)的图象是C，则

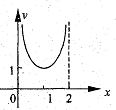A.与y轴平行的直线与C最多只有一个公共点　　　　　　　　 

B.与y轴平行的直线与C可以有两个以上的公共点

C.与x轴平行的直线与C最多只有一个公共点

D.与x轴平行的直线与C不可能有无数个公

10.函数f(x)的图象如右图所示，则y=log_0.2f(x)的图象的示意图为

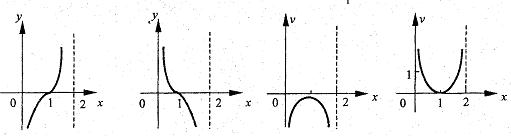
　 A　　　　　　　　　 B　　　　　　　　  C　　　　　　　　  D

11.某服装商贩同时卖出两套服装，售价为160元/套，以成本计算，一套盈利20%，而另一套亏损20%。则此商贩

A.不赚也不赔　　　　  B.赚14元　　　　 C.赔14元　　　　 D.赚37.2元

12.一个只有有限项的等差数列，它的前5项的和为34，最后5项的和为146，所有项的和为234，则它的第7项等于

A.22　　　　　　　　  B.21　　　　　　  C.19　　　　　　  D.18

二、填空题(本大题共4小题，每小题4分，共16分，请将答案直接填在题中的横线上)

13.已知P：│3x-4│＞2 q:＞0, 则┐p是┐q的什么条件？　　　　　　  。

3.函数y=的反函数的奇偶性为　　　　　 ，在（0，+）上的单调性为　　__ 。

14.若a₁,a_2, a₃……a_2n+1成等差数列，奇数项和为60，偶数项和为45，则该数列的项数为 ___ 。

15．f（x）=log_a（ax²-x）在区间［2，4］上是增函数，则a的范围是_________________。

16．若数列｛a_n｝的前n项和Sn=log（1+n），则a10+a11+…+a99=_________________。

三、解答题（本大题共6小题，共74分。解答应写出必要的文字说明、证明过程或演算步骤）

17．（本小题12分）作出函数y=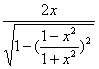的图像

18．（本小题12分）已知f（x）=　 （1）求证：f（-x）+f（x）=0。（2）判断单调性并求值域。（3） 解不等式0＜f（x²-x-2）＜

19．（本小题12分）农产品去年各季度的市场价格如下表：

季　 度	第一季度	第二季度	第三季度	第四季度
每吨售价 （单位：元）	195.5	200.5	204.5	199.5

今年某公司计划按去年各季度市场价格的“平衡价m”（平衡价m是这样的一个量：与上年各季度售价差比较，m与各季度售价差的平方和最小）收购该种农产品，并按每100元纳税10元（又称征税率为10个百分点），计划可收购a万吨，政府为了鼓励收购公司多收购这种农产品，决定将税率降低x个百分点，预测收购量可增加2x个百分点.

　 （Ⅰ）根据题中条件填空，m=　　　　   （元/吨）

　 （Ⅱ）写出税收y（万元）与x的函数关系式；

　 （Ⅲ）若要使此项税收在税率调节后不少于原计划税收的83.2%，试确定x的取值范围.

20．（本小题12分）三个互不相同的实数是等比数列｛an｝中的连续三项，并且它们依次又为一等差数列中的第2项，第9项和第44项，这三个数的和为217，（1）求这三个数。（2）Sn为等比数列的前n项和且＜＜，求n的值。

21．（本小题12分）设二次函数f(x)=x²+x+c(c＞0)，若方程f(x)=0有两个实数根x₁,x₂(x₁＜x₂).

（1）求c的取值范围；

（2）求x₂－x₁的取值范围；

（3）如果存在一个实数m，使得f(m)＜0，求证：m+1＞x₂.

22．（本小题14分）已知函数f（x）=lg（a^x-kb^x）（k∈R⁺，a＞1＞b＞0）的定义域恰为区间（0，+∞）上取正值，且f（3）=lg4？若存在求出a，b的值，若不存在，请说明理由。

综合练习四参考答案

一、选择题：

1	2	3	4	5	6	7	8	9	10	11	12
C	C	D	A	B	A	C	A	A	C	C	D

二、填空题：

 13充分不必要条件　14，7　　 15，a＞1　　　 16，-1

三、解答题：

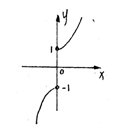17．∵1-（）²＞0　∴-1＜＜　∴x≠0

∴y==　　　　　　

18．（1）∵x∈R　又∵f（-x）==-f（x） ∴f（-x）+f（x）=0

（2）∵f（x）=1- ∵2^x+1在（-∞，+∞）上递增　∴在R上递减

∴f（x）在k上递增

∵2^x+1＞1　 ∴0＜＜1　∴-2＜＜0　∴-1＜1-＜1

∴f（x）值域为（-1，1）

（3）∵f（0）=0　　f（4）=　 ∴原不等式化为　　f（0）＜f（x²-x-2）＜f（4）

∵f（x）在R上为增函数　∴0＜x²-x-2＜4　 ∴

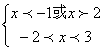∴　 ∴解集为（-2，-1）U（2，3）

19．（I）200；

　 （II）降低税率后的税率为（10－x）%，农产品的收购量为a（1+2x%）万担，收购总金额为200a（1+2x%）故y=200a（1+2x%）（10－x）%=

　　　　　　　 

　　（III）原计划税收为200a×10%=20a（万元），依题意得：

　　　　　　　

　　　　　　　答：x的取值范围是0<x≤2.

 

20．①设这三个数为a、aq、aq²则a+aq+aq²=217

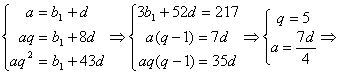∴a=7

∴这三个数为7，35，175

②＜　 ∴24＜5ⁿ-1＜624

∴25＜5ⁿ＜625　　∴2＜n＜4　　∵n∈N^*　 ∴n=3

21．（1）由方程x²+x+c=0有两个实数根x₁,x₂(x₁＜x₂)及c＞0,得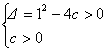解得0＜c＜.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　4分

（2）根据根与系数的关系，得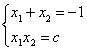　　　　　　　　　　　　　　　　　　　　　　　　　6分

又x₂－x₁＞0,所以,

x₂－x₁==,

所以0＜x₂－x₁＜1. 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 8分

（3）因为f(m)＜0,且抛物线f(x)=x²+x+c的开口向上，

所以x₁＜m＜x₂，所以m－x₁＞0,　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　10分

从而m+1＞m+(x₂－x₁)=(m－x₁)+x₂＞x₂.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

22．

解：设存在a＞1＞b＞0满足条件

∵定义域恰为（0₁，+∞）即a^x-kb^x＞0解集为x＞0　 ∵a＞1

∴1-k（）^x＞0　 ∴k（）^x＜1　∴（）^x＜　 ∴=1　　∴k=1

∵f（x）＞0在（1，+∞）上恒成立 即a^x-b^z＞1 在（1，+∞）上恒成立

∴x=1时 a-b=1

∵f（3）=lg（a³-b³）=lg4　　∴a³-b³=4　由　 ∴