广州市真光中学2004学年度第二学期高一级数学测试题
(必修3学分认定考试 总分:100分 时间:90分钟)
班级: 学号: 姓名: 成绩___________
一、选择题(共12小题,每题4分,共48分)
1.为了解1200名学生对学校某项教改试验的意见,打算从中抽取一个容量为30的样本,考虑采用系统抽样,则分段的间隔k为( )。
A. 40 B. 30 C. 20 D. 10
2. 一个容量为20的样本,组距与频数如下:
( 10
, 20 ] , 2 ; (
20 , 30 ] , 3 ; (
30 , 40 ] , 4 ;
( 40
, 50 ] , 5 ; (
50 , 60 ] , 4 ; (
60 , 70 ] , 2 ;
则样本在( -∞ , 50
]上的频率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3.10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为![]() ,中位数为
,中位数为![]() ,众数为
,众数为![]() ,则有( )
,则有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. 算法的三种基本结构是( )
A.顺序结构,条件分支结构,重复结构
B.逻辑结构,模块结构,分支结构
C.矩形结构,菱形结构,平行四边形结构
D.顺序结构,条件结构,循环结构
5.如图1是一个循环结构的算法,下列说法不正确的是( )
A.①是循环变量初始化,循环将要开始;
B.②为循环体;
C.③是判断是否继续循环的终止条件;
D.③中“是”与“否”的位置交换对算法没影响
|
|
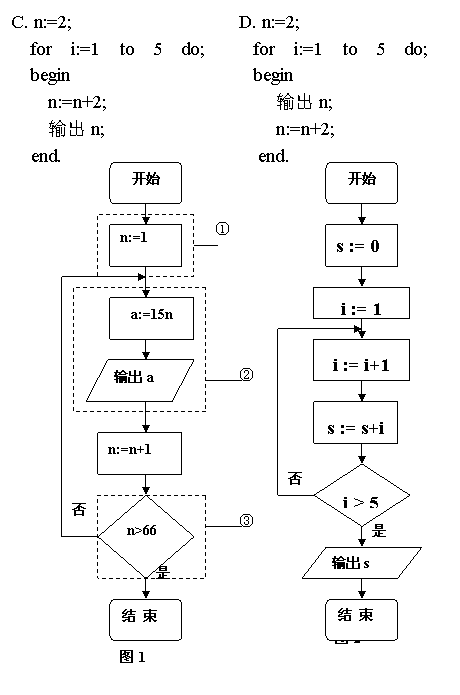 |
7.如图2所示的算法流程图,最后输出的s值为( )。
A. 14 B. 15 C. 20 D. 21
8.把由m个数据组成的无序列用冒泡排序法排成有序列,最多需要经过
( )趟排序过程。
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9.下列说法正确的是( )
A.掷一枚硬币,出现正面朝上的概率是0.5,因此掷一枚硬币10次,恰好出现5次正面向上;
B.连续四次掷一颗骰子,都出现6点是不可能事件;
C.一个射手射击一次,命中环数大于9与命中环数小于8是对立事件;
D.若P(A+B)=1,则事件A与B为对立事件。
10.下列试验中,是古典概型的有( )
A.某人射击中靶或不中靶
B.在平面直角坐标系内,从横坐标和纵坐标都为整数的所有点中任取一个
C.四位同学用抽签法选一人参加会议
D.运动员投篮,观察是否投中
11.掷两颗骰子,设出现点数之和为12,11,10的概率依次为![]() ,则
,则
( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
12. 不透明的袋中装有100个大小相同的红球、白球和黑球,其中42个红球,从口袋中摸出一个球,摸出白球的概率是0.23,则摸出黑球的概率是
( )。
A. 0.32 B. 0.35 C. 0.65 D. 0.19
二、填空题(共4题,每题3分,共12分)
13.如果数据![]() 的平均数是
的平均数是![]() ,那么
,那么![]() =____________。
=____________。
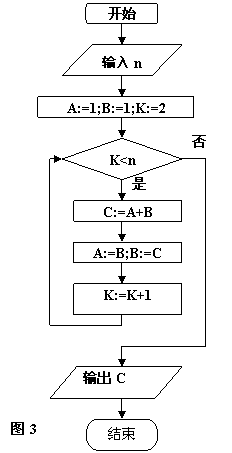
14.图3是求某种运算的流程图,计算当n=7时输出结果C的值为__________。
15.不透明的袋中装有2个白球、2个黑球、2个红球、2个绿球,无放回地从袋中抽4次球,每次抽一个,则第三次抽出红球的概率为__________。
16.一个不透明的袋中有一定数目的白球和红球,无放回地任抽两个都为红球的概率为0.28,则抽到至少一个为白球的概率为_________。
三、简答题(共4小题,共40分)
17.为了解各自受欢迎的程度,甲、乙两个网站分别随机选取14天,记录了上午8:00~10:00间各自的点击量如下:
甲:73,24,58,72,64,38,66,70,20,41,55,67,8,25
乙:12,37,21,5,54,42,61,45,19,6,19,36,42,14
(1) 请你用茎叶图表示上面的数据;
(2) 甲、乙两个网站哪个更受欢迎?
18.编写一个算法流程图,对于函数
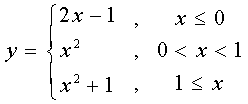 输入x的值,输出相应的函数值,并用基本语句表示此算法。
输入x的值,输出相应的函数值,并用基本语句表示此算法。
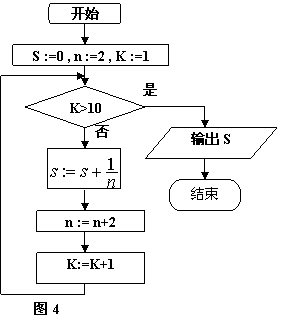
19.如图4是某一算法流程图。
(1) 请用for语句表示该算法(4分)
(2) 请用repeat语句表示该算法(4分)
(3) 请指出这一算法的功能(2分)
20.摇两颗骰子,求下列事件发生的概率:
(1) 两颗骰子向上点数一样;
(2) 两颗骰子向上点数和大于6;
(3) 两颗骰子向上点数和为3的倍数;
(4) 两颗骰子向上点数和为偶数;
(5) 两颗骰子向上点数和小于7。