正余弦的诱导公式
复习要求1：熟练掌握正弦，余弦诱导公式并运用它求任意角的三角函数值，化简，简单三角恒等式的证明。
2：了解把未知问题化归为已知问题的数学思想，提高解题能力。
复习重点：诱导公式及其综合运用。
复习过程： 一：基本公式
1:sin(360k+a)=________________ cos(360k+a)=_______________________
2:sin(180+a)=________________ cos(180+a)=________________________
3:sin(90+a)=__________________ sin(270+a)=_________________________
4:cos(90+a)=__________________ cos(270+a)=________________________
以上四组公式可概括为360k+a,180+a (或90+a, 270+a) 的三角函数值，等于a 的同名（或余名）函数值，前面加上把a看成锐角时原函数值的符号：简记为：“奇变偶不变，符号看象限。”
二：公式的主要运用1：任意角的三角函数转化为锐角三角函数。
2：三角函数式的化简。3：三角恒等式的证明。
三：基础练习〈1〉： tan
+cot(-
)的值是
〈2〉： 已知sin(
-a)=
,则 sin(a-
)的值等于
〈3〉：设 a 是第三象限角，则
=
〈4〉：已知A=
+
(k∈Z), 则 A 值构成集合
四：例题分析
例1 求 sin315sin(-1260 )+cos570 sin(-840 ) 的值。
例2 已知 tan(+a)=3 ,求
的值。
例3 已知A,B,C为三角形的三个内角，求证〈1〉cos(2A+B+C)= --cosA
<2>tan
=--tan
跟踪练习
1：计算 sin
cos
tan( 
)
2:已知 cos(a+75 )=
,a 为第三象限角，求cos(15 –a)+sin(a-15 ) 的值。
3：证明
=-tana
五：作业
1：设f(n)=cos
,求f(25)+f(26)+f(27)+…..+f(42)的值
2：化简 sin(
-a)+cos(
),其中n
,a
(0,)
3:已知sina是方程５
-7x-6=0的根，求
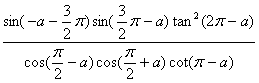的值。
４：在三角形ABC中，若sin(A+B-C)=sin(A-B+C),试判断三角形ABC的形状。