综合训练(第5章平面向量)

综合训练(第5章 平面向量)

1.下列命题不正确的是

A.若a≠λb,则a、b不共线（λ∈R）

B. b=3a（a≠0）,则a、b共线

C.若a+b+c=0,则a+b=－c

D.若m=3a+4b,n=a+2b,则m∥n

【解析】 若a≠0,b=0,则a≠λb,但a与b共线.

【答案】 A

2.下列关系式正确的是

A.+=0

B.a·b是一个向量

C. － =

D.0· =0

【解析】 ∵ =－，∴+=0.

又a·b、0·都为实数,所以B、D错误.

又－； =，∴C错误.

【答案】 A

3.若a=2，b=,a·b=，则a与b的夹角

A.30°　　　　　　　　　　　　　　　　　B.45°　　　　　　　　　C.60°　　　　　　　　　　　　 D.120°

【解析】 设a、b夹角为θ，则由

a·b=a·bcosθ得： =2· cosθ

∴cosθ=，又0°≤θ≤180°，

∴θ＝60°

【答案】 C

4.已知点A（x,5）关于点（1，y）的对称点是B（－2，－3），则点（x,y）到原点的距离是

A.　　　　　　　　　　　　B.　　　　　　　　　　　　C.4　　　　　　　　　　　　　　　D.

【解析】 由中点坐标公式知；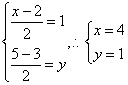

再由两点间距离公式得:.

【答案】 D

5.若a=（0,1）,b=（1,1）,且（a+λb）⊥a，则λ的值是

A.－1

B.0

C.1

D.2

【解析】 a+λb=（0,1）+λ（1,1）=（λ,1+λ）又（a+λb）⊥a,

∴λ×0+（1+λ）×1=0

∴λ=－1

【答案】 A

6.在△ABC中，D、E、F分别是AB、BC、CA的中点，则－

A.

B.

C.

D.

【解析】 －=－= （－）==.

【答案】 D

7.若=3e,=－5e且｜｜=｜｜,则四边形ABCD是

A.平行四边形

B.等腰梯形

C.菱形

D.不等腰的梯形

【解析】 由已知得：=－,故与平行且方向相反，且｜｜＞

｜｜,再由｜｜=｜｜,可知ABCD是等腰梯形.

【答案】 B

8.已知△ABC，a=5,b=8,C=60°，则·=___________.

【解析】 ·=cos（π－C）=abcos120°=5×8×（－）=－20

【答案】 －20

9.已知a=3,b=4,a·b=－2,则a+b=___________.

【解析】 a+b²=（a+b）²=a²+2a·b+b²=9+2×（－2）+16=21

∴a+b=

【答案】  

10.已知a=（3,0）,b=（k,5）,且a、b的夹角为,则k的值为___________.

【解析】 a·b=3k,｜a｜=3,｜b｜=,cosθ=cos=－.

由cosθ=得－=,

∴=－k,

∴.

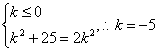【答案】 －5

11.已知a+b=2i－8j, a－b=－8i+16j,那么a·b=___________（其中i,j为两个互相垂直的单位向量）.

【解析】 由已知可得a=－3i+4j,b=5i－12j,

∵i²=j²=1,i·j=0,

∴a·b=（－3i+4j）·（5i－12j）=－15i²+56i·j－48j²

=－15－48=－63.

【答案】 －63

12.设点A（3,－4）,B（1,2）,P是直线上的一点,且=2,则点P坐标是___________.

【解析】 由=2得: =±2

∴=±2,

∴λ==±2

当λ=2时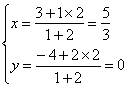

当λ=－2时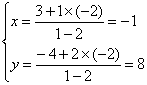

∴P点坐标为（,0）或（－1,8）

【答案】 （,0）或（－1,8）

13.将抛物线y=x²+6x+11的图象经过向量a平移得到y=x²，则a=___________.

【解析】 y=x²+6x+11=（x+3）²+2

∴y－2=（x+3）²

令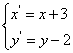得：y′=x′²，

∴a=（3,－2）

【答案】 （3,－2）

14.在△ABC中，b=,c=3,B=30°，则a=___________.

【解法一】 由余弦定理得

b²=a²+c²－2accosB得

a²－3a+6=0解得a=或a=2

【解法二】 由得sinC=

∴C=60°或C=120°

由正弦定理得：a=或a=2

【答案】 或2

15.设O为原点,=（3,1）,=（－1,2）,⊥,∥,试求满足+ =的的坐标.

【解】 设 =（x,y）,

则=+ =（x+3,y+1）

=－ =（x+4,y－1）

由⊥,得－（x+3）+2（y+1）=0

即x－2y+1=0　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

由∥,得3（y－1）－（x+4）=0

即x－3y+7=0　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ②

由①②联立,解得x=11,y=6

即坐标为（11,6）.

16.已知a、b、c是△ABC的三边，且满足2lg（a²+b²－c²）=lg2+2lga+2lgb,求证：∠C=.

【解】 ∵2lg（a²+b²－c²）=lg2+2lga+2lgb

∴（a²+b²－c²）²=2a²b²

∴,

∴

又a²+b²－c²＞0,a＞0,b＞0,

∴,

∴cosC=,

∴∠C=.

17.将二次函数y=px²+qx+r的图象按向量a=（3,－4）平移后,得到的图象的解析式为y=2x²－3x+1,试求p、q、r的值.

【解】 将二次函数y=px²+qx+r的图象按向量a=（3,－4）平移后得到的图象的解析式为:y+4=p（x－3）²+q（x－3）+r,

即y=px²+（q－6p）x+9p－3q+r－4,

它就是y=2x²－3x+1.

∴,

解之得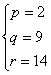

18.设i,j是平面直角坐标系中x轴和y轴方向上的单位向量,=4i－2j,=7i+4j, =3i+6j,求四边形ABCD的面积.

【解】 ∵=+,

∴四边形ABCD是平行四边形（或用=－=证明ABCD是平行四边形），

又∵·=2（2i－j）·3（i+2j）=6（2i²+3i·j－2j²）=0,

∴⊥,即ABCD是矩形.

∴S_ABCD=｜｜｜｜==30.

19.设两个向量a、b不共线,

（1）若=a+b,=2a+8b,=3（a－b）,求证A、B、D三点共线；

（2）若a=2,b=3,a、b的夹角为60°,求使向量ka+b与a+kb垂直的实数k.

（1）【证明】  =++ =a+b+2a+8b+3（a－b）=6（a+b）=6

∴与共线,又与有公共点A，

∴A、B、D三点共线.

（2）【解】 ka+b与a+kb垂直,

即（ka+b）·（a+kb）=0

ka²+（k²+1）a·b+kb²=0

ka²+（k²+1）abcos60°+kb²=0

3k²+13k+3=0,

解得k=.