深圳市教苑中学高一年级期末复习综合测试(一)
第一卷
一、选择题(每小题5分,共60分)
1、点P在直线a上,直线a在平面α内可记为( )
A、P∈a,a![]() α B、P
α B、P![]() a,a
a,a![]() α C、P
α C、P![]() a,a∈α D、P∈a,a∈α
a,a∈α D、P∈a,a∈α
2、直线l是平面α外的一条直线,下列条件中可推出l∥α的是( )
A、l与α内的一条直线不相交 B、l与α内的两条直线不相交
C、l与α内的无数条直线不相交 D、l与α内的任意一条直线不相交
3.直线![]() x+y+1=0的倾斜角为 ( )
x+y+1=0的倾斜角为 ( )
A.50º B.120º C.60º D. -60º
4、在空间中,l,m,n,a,b表示直线,α表示平面,则下列命题正确的是( )
A、若l∥α,m⊥l,则m⊥α B、若l⊥m,m⊥n,则m∥n
C、若a⊥α,a⊥b,则b∥α D、若l⊥α,l∥a,则a⊥α
5、函数y=log2(x2-2x-3)的递增区间是( )
(A)(-![]() ,-1) (B)(-
,-1) (B)(-![]() ,1) (C)(1,+
,1) (C)(1,+![]() ) (D)(3,+
) (D)(3,+![]() )
)
6.设函数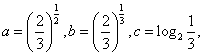 则
则![]() 的大小关系是( )
的大小关系是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
7、如果![]() 且
且![]() ,那么直线
,那么直线![]() 不通过( )
不通过( )
A 第一象限 B 第二象限 C 第三象限 D 第四象限
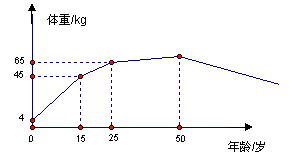 8, 右图表示某人的体重与年龄的关系,则
(
)
8, 右图表示某人的体重与年龄的关系,则
(
)
A. 体重随年龄的增长而增加
B. 25岁之后体重不变
C. 体重增加最快的是15岁至25岁
D. 体重增加最快的是15岁之前
9,计算![]()
A. 20 B. 22 C. 2 D. 18
10、经过点A(1,2),且在两坐标轴上的截距相等的直线共有( )
A 1条 B 2条 C 3条 D 4条
11、已知A(2,![]() ,B (
,B (![]() ),直线
),直线![]() 过定点P(1, 1),且与线段AB交,则直线
过定点P(1, 1),且与线段AB交,则直线![]() 的斜率
的斜率![]() 的取值范围是( )
的取值范围是( )
A ![]() B
B ![]() C
C ![]() D
D ![]() 或
或![]()
12、A,B,C,D四点不共面,且A,B,C,D到平面α的距离相等,则这样的平面( )
A、1个 B、4个 C、7个 D、无数个
深圳市教苑中学高一年级期末复习综合测试(一)
第二卷
一,选择题答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | D | B | D | D | C | D | B | C | B | D | C |
二、填空题(每小题5分,共20分)
13、在空间四边形ABCD中,E,H分别是AB,AD的中点,F,G为CB,CD上的点,且CF∶CB=CG∶CD=2∶3,若BD=6cm,梯形EFGH的面积 28cm2,则EH与FG间的距离为 8cm 。
14、a,b为异面直线,且a,b所成角为40°,直线c与a,b均异面,且所成角均为θ,若这样的c共有四条,则θ的范围为 (70°,90°) 。
15,点P(2,5)关于直线 x+y=0 的对称点坐标是 (-5,-2) .
16,m为任意实数时,直线(m-1)x+(2m-1)y=m-5必过定点 (9,-4) .
三,解答题(本大题有6小题,共70分)
17.(10分)设 a>0,且a≠1,解关于x的不等式a![]() >a
>a![]()
![]()
![]()
![]() -------5分
-------5分
![]()
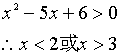
-------10分
18.(12分) △ABC的两顶点A(3,7),B(![]() ,5),若AC的中点在
,5),若AC的中点在![]() 轴上,BC的中点在
轴上,BC的中点在![]() 轴上。(1)求点C的坐标;(2)求AC边上的中线BD的长及直线BD的斜率 。
轴上。(1)求点C的坐标;(2)求AC边上的中线BD的长及直线BD的斜率 。
解:(1)设![]() ,
,![]()
![]()
![]() ----------6分
----------6分
![]()
![]() ----------12分
----------12分
19.(14分)已知函数f(x)=![]() .
.
(1)求f(x)的定义域;
(2)判断并证明f(x)的奇偶性。
(3)若![]()
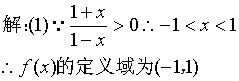
-----5分
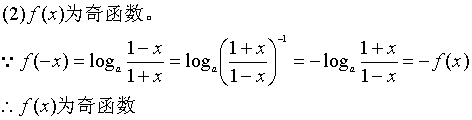
-----10分
![]()
-----12分
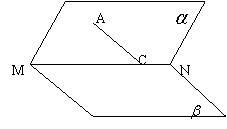
20.(12分)如图,![]() MN,A
MN,A![]() ,C
,C![]() MN,且∠ACM=
MN,且∠ACM=![]() ,
,![]() 为
为![]() ,AC=1,求A点到
,AC=1,求A点到![]() 的距离。
的距离。
解:![]()
![]() -------4分
-------4分
![]()
![]()
![]()
![]() D
D
![]() B
B
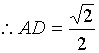 ---8分
---8分
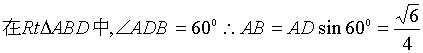 -----12分
-----12分
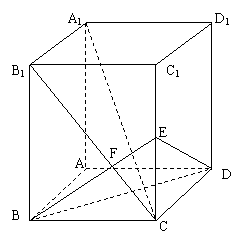 21.(14分)已知长方体AC1中,棱AB=BC=3,棱BB1=4,连结B1C,过B点作B1C的垂线交CC1于E,交B1C于F.
21.(14分)已知长方体AC1中,棱AB=BC=3,棱BB1=4,连结B1C,过B点作B1C的垂线交CC1于E,交B1C于F.
(1)求证A1C⊥平面EBD;
(2)求二面角B1—BE—A1的正切值.

―――――――6分

――――――――8分
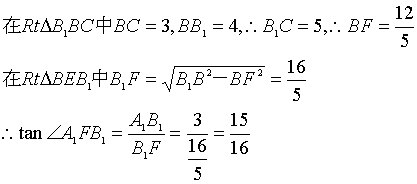
―――――12分
22.(14分)已知![]() 是定义在
是定义在![]() 上的增函数,且
上的增函数,且![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,解不等式
,解不等式![]() .
.
![]() ---------3分
---------3分
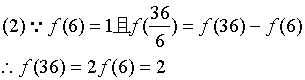
----------7分
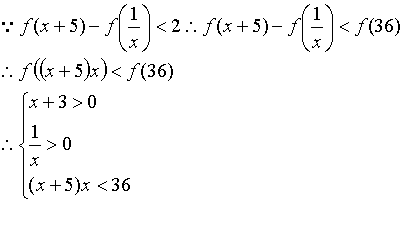
--------10分
![]() --------12分
--------12分