江西省宜丰中学高一下学期第一次月考
数 学 试 卷
一、选择题：（每小题５分，共60分）
1、sin1320º的值是( )。
A、
B、
C、
D、
2、如果一扇形的圆心角为72º，半径等于20cm。则扇形的面积为（ ）。
A、40πcm2 Ｂ、80πcm2 Ｃ、80cm2 Ｄ、40cm2
3、已知角α的终边过点P(4,-3)。则 2sinα+cosα=( )。
Ａ、
Ｂ、
Ｃ、－
Ｄ、
4、(１＋tan21º)(１＋tan22º)(１＋tan23º)(１＋tan24º)的值为。
Ａ、2 Ｂ、4 Ｃ、8 Ｄ、16
5、化简
＝( )。
Ａ、cos5+sin5 Ｂ、-cos5-sin5 Ｃ、－cos5+sin5 Ｄ、cos5-sin5
6、已知tanα=，则
的值为( )。
Ａ、10 Ｂ、-10 Ｃ、
Ｄ、
7、已知x∈(－,0)，cosx＝，则tan2x等于( )。
A． B．－ C． D．－
8、设
，
，
则有（ ）。
Ａ、a>b>c Ｂ、a<b<c Ｃ、a<c<b Ｄ、b<c<a
9、下列各式中，①
,②
,③
.其中值为１的个数是（ ）。
Ａ、0个 Ｂ、1个 Ｃ、2个 Ｄ、3个
10、△ABC中,①sin(A+B)+sinC, ②
③cos(B+C)+cosA④
,其中恒为常数的是_________________。
Ａ、①③ Ｂ、③④ Ｃ、①②③④ Ｄ、②③④
11、已知点Ｐ（sinα-cosα,tanα）在第一象限，则在[0,2π)内α的取值范围是（ ）。
Ａ、
Ｂ、
Ｃ、
Ｄ、
12、已知α.β是锐角，sinα＝x，cosβ＝y，cos(α＋β)＝－，则y与x的函数关系式为( )。
A.y＝―＋x 
B.y＝―＋x
C.y＝――x D.y＝――x
二、填空题：（每小题4分，共16分）
13、已知:
，则角α的终边在第______ 象限。
14、设函数f(x)=asin(πx+α)+bcos(πx+β)，a、b、α、β都是非零实数，且满足f(2005)=-1，则f(2006)= ______________ 。
15、已知α+β+γ=90˚，则
=___________。
16、设α、β、γ为锐角，sinα+sinγ=sinβ，cosβ+cosγ=cosα。则
α-β=___________。
三、解答题：共74分
17、已知α为第二象限角，sinα=；β为第一象限角，cosβ=
。求tan(α-β)的值。(12分)
18、已知：5sinβ=sin(2α+β).求证：2tan(α+β)=3tanα。 (12分)
19、已知tan(
+θ)=3,求sin2θ-2cos2θ。(12分)
20、化简：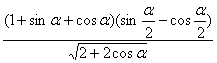
(π<α<2π)。（12分）
21、设tanα、tanβ是方程x2-3x-3=0的两个实根。求sin2(α+β)-3sin(α+β)cos(α+β)-3 cos2(α+β)的值。（12分）
22、△ABC中，满足:①三内角A、B、C成等差数列 ②
。求cos
的值。(14分)
江西省宜丰中学高一下学期第一次月考数学试题答案
一、 选择题：（每小题5分，共60分）
1、C 2、B 3、C 4、B 5、B 6、C 7、D 8、C 9、D 10、B 11、B 12、A
二、 填空题：（每小题4分，共16分）
13、四 14、 1 15、 1 16、 
三、 解答题：
17、解：∵α为第二象限角，
∴
∴
∵β为第一象限角，
∴
∴
∴
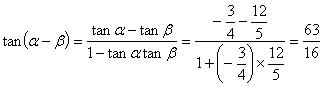
18、证明：∵
∴
展开：
两边同除以２
得：
19、解：∵
∴
∴
∴
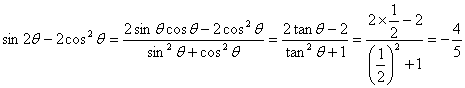
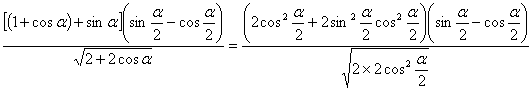
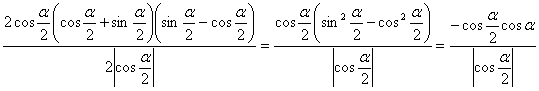
20、原式
=
=
∵
∴
∴
∴原式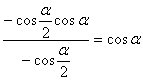
21、解：由已知条件及根与系数关系得：
，
∴
原式=
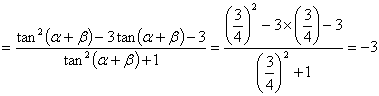
22、解：（法一）
A+B+C=180°且A+C=2B 得:B=60°,A+C=120°
∴ 原式可化为：cosA+cosC=
利用和差化积与积化和差公式，上式可化为：
由A+C=120°,代入上式得：
最后化简得：
即：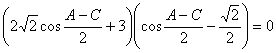
由于
∴
,即：
。
（法二） 由已知条件有 B=60˚ Ａ＋Ｃ＝120˚, 令
即
有
∴
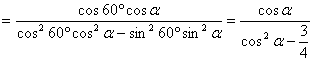
根据题设条件: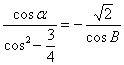
∵
∴
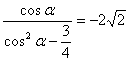
整理为 
即: 
又 
∴
得: