线段的定比分点
复习要求 1:理解有向线段定比分点的概念。2:熟练运用有向线段的定比分点和中点坐标公式解决简单问题。
复习重点 定比分点公式的运用
复习过程
一:知识回顾
1:定比分点的定义:设![]() ,P
,P![]() 是直线l上的两点,点P是l上不同于
是直线l上的两点,点P是l上不同于![]() ,P
,P![]() 的任意一点,则存在一个实数
的任意一点,则存在一个实数![]() ,使得
,使得 ![]() =
=![]() ,
,![]() 叫做点P分有向线段
叫做点P分有向线段![]() 所成的比。
所成的比。
2:定比分点的坐标表示式:设P![]() (x
(x![]() ,y
,y![]() ) , P (x
) , P (x![]() ,y
,y![]() ),P (x , y)且
),P (x , y)且![]() =
=![]() 则
则 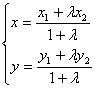 (
(![]() ) ,特别当
) ,特别当 ![]() =1时,得
=1时,得![]() ,P
,P![]() 的中点P的坐标公式:
的中点P的坐标公式: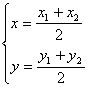
3:定比分点的向量表示式:在平面内任取一点O,设OP![]() =a , OP
=a , OP![]() =b,则由
=b,则由![]() =
=![]() 得
得![]() =
=![]() (
(![]() ) ,此式叫定比分点的向量公式。当P为线段
) ,此式叫定比分点的向量公式。当P为线段 ![]() P
P![]() 的中点时,
的中点时,![]() =1,此时OP为三角形O
=1,此时OP为三角形O![]() P
P![]() 的中线且
的中线且![]() =
=![]() .
.
二:知识的主要运用 1.求分点的坐标。2.求定比![]() 的值。3.利用线段中点公式解题。
的值。3.利用线段中点公式解题。
三:基础训练
1:已知点A(m,-n),B(-m,n)点C分有向线段![]() 的比为-2,则C点的坐标为( )
的比为-2,则C点的坐标为( )
A(-3m,3n) B (m,n) C (3m,3n) D (-m,n)
2.已知点P分有向线段![]() 的比是-3,则点P
的比是-3,则点P![]() 分
分![]() 所成的比为( )
所成的比为( )
A -![]() B -
B -![]() C -
C -![]() D -
D -![]()
A (4,-3) B(![]() ,0) C(-
,0) C(-![]() ,3) D(6,-9)
,3) D(6,-9)
4.已知点A(2,3),点B(10,5),直线AB上一点P满足![]() =2
=2![]() ,则
,则
P点的坐标是( )
A (![]() ,
,![]() ) B(18,7) C(
) B(18,7) C(![]() ,
,![]() )或(18,7) D(-6,1)或(18,7)
)或(18,7) D(-6,1)或(18,7)
四:典型例题
例1. 已知A(-1,1),B(1,3),C(4,6),(1)求证:A,B,C三点共线;
(点C分![]() 所成的比
所成的比![]() ;(3)求点A分
;(3)求点A分![]() 所成的比
所成的比![]()
例2.已知三角形ABC的两顶点A(3,7),B(-2,5)且AC的中点在x轴上,BC的中点在y轴上,求C点的坐标
例3.知A(2,3),B(0,1),C(3,0),点D,E分别在AB,AC上,DE//BC 且DE平分三角形ABC的面积,求点D的坐标
五:跟踪练习
1. 若点C为有向线段![]() 上靠近A点的三等分点,则点B分有向线段
上靠近A点的三等分点,则点B分有向线段![]() 所成的比为
所成的比为
2. 已知点A(x,5)关于点C (1,y)的对称点是B(-2,-3),则点P(x,y)到原点的距离
是
3.已知矩形ABCD的两相邻顶点坐标是A(-1,3),B(-2,4),若该矩形对角线交点M在x轴上,则另外两顶点坐标为
五.作业巩固
1. 已知三点A(0,8),B(-4,0),C(5,-3),D点内分有向线段
![]() 的比为
的比为
1:3,E在BC上且使三角形BDE的面积是三角形ABC面积的一半,求E点的坐标
2已知点A (1,-1),B(-4,5),点C在直线AB上,且![]() =3
=3![]() ,求
,求![]() 的坐标
的坐标