华中师大一附中上学期高一年级数学期末试题
限时:120分钟 满分:150分 命题人:胡 敏 审题人:罗道珍
第I卷(选择题共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将你认为正确的选项代号填在第II卷的答题卡内.
1.设集合![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设![]() ( )
( )
A.2条 B.4条 C.6条 D.8条
3.不等式![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知![]() ( )
( )
A.2 B.4 C.![]() D.
D.![]()
5.已知![]() ( )
( )
A.4, 10 B.0, 4 C.![]() D.1,10
D.1,10
6.设角![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.数列![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.设![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.函数![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.若![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.各项为正数的数列![]()
![]() 的值为
( )
的值为
( )
A.4 B.-4 C.2 D.-2
12.设函数![]()
件是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
第II卷(非选择题共90分)
分数
选择题答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.
13.设函数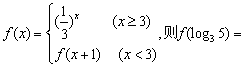 .
.
14.已知点(2,1)在函数![]() .
.
15.在等比数列![]() .
.
16.有下面四个命题:
(1)“若xy=1,则x,y互为倒数”的逆命题
(2)“全等三角形的周长相等”的否命题
(3)“若![]() ”的逆否命题
”的逆否命题
(4)若![]() .
.
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17.(本题满分12分)
设数列![]()
(1)求数列的通项公式an
(2)求![]()
18.(本题满分12分)
设函数![]()
(1)若![]()
(2)若![]()
19.(本题满分12分)
将数列![]()
(1)数46是在第几组?
(2)第n组的各数之和Sn.
20.(本题满分12分)
某企业2001年年初投入资金100万元,若该企业经过有效经营能使每年资金平均增长50%,但每年底又要扣除消费基金x万元,余下投入再生产. 设每年底余下的资金(万元)记为数列{an},问:
(1)第一年底余下的资金a1=
第二年底余下的资金a2= (填空)
(2)为实现2004年年底的资金不低于425万元(扣除消费基金后),求x的最大值.
21.(本题满分12分)
设函数![]()
(1)若![]()
(2)若![]()
22.(本题满分14分)
对任意函数![]()
 (1)输入数据
(1)输入数据![]() 经数列发生器输出
经数列发生器输出![]()
(2)若![]() 则数列发生器结束工作.若
则数列发生器结束工作.若![]() 则
则
将![]() 反馈回输入端,再输出
反馈回输入端,再输出![]() 继续
继续
下去.现定义![]() ,请解答:
,请解答:
[1] 若输入![]() , 则由数列发生器产生数列
, 则由数列发生器产生数列![]() ,
,
写出数列{xn}的所有项.
[2] 若要数列发生器产生一个无穷常数列. 求输入的数据x0的值.
[3] 若输入x0时, 产生无穷数列{xn}满足:对任意正整数n, 均有
![]() 求x0的取值范围.
求x0的取值范围.
华中师大一附中2004—2005学年度上学期
高一年级数学期末试题参考答案
一、选择题:(5′×12=60′)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | A | C | B | D | B | C | C | D | A | B |
二、填空题:(4′×4=16′)
13.![]() 14.
14.![]() 15.
15.![]() 16.①③④
16.①③④
三、解答题:
17.(1)当![]()
当![]()
![]() ………………………………………………………(6分)
………………………………………………………(6分)
(2)当![]() 当
当![]()
![]()
![]() ……………………………………(12分)
……………………………………(12分)
18.(1)当![]()
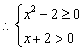 …………(i)或
…………(i)或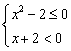 …………(ii)
…………(ii)
由(i)得![]()
由(ii)得![]()
∴原不等式解集为![]() ……………………………(6分)
……………………………(6分)
(2)设任意![]()
则![]()
![]()
∵![]()
![]()
![]()
即![]() 恒成立.
恒成立.
由![]()
![]()
故![]() ………………………………………………………………(12分)
………………………………………………………………(12分)
19.(1)将各组数展开,得一等差数列,首项为1,公差为3.
令![]()
设46位于第k组.
![]()
![]()
解得k=6
(或![]() )
)
即46位于第6组………………………………………………………………(5分)
(2)前n组共有![]()
记前n组的各数之和为Tn, 则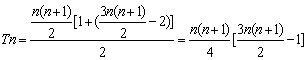
∴第n组各数之和
![]()
当![]()
![]() ……………………………(12分)
……………………………(12分)
20.(1)a1=150-x , a2=225-2.5x ……………………………………………………(4分)
(2)(法1)2004年底余下资金
![]()
![]()
解得![]() …………………………………………(12分)
…………………………………………(12分)
(法2)第3年后余下的资金
![]()
∴第4年(即2004年)底余下的资金为![]() (余下同)
(余下同)
21.(1)![]()
∴当a=1时,满足
当a≠1时,由
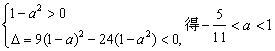
∴综上可得![]() ……………………………………………………(5分)
……………………………………………………(5分)
(2)∵![]()
![]()
由![]()
比较系数得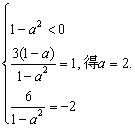
当![]()
![]()
![]()
即![]() ………………………………………………(12分)
………………………………………………(12分)
22.(1)![]()
![]() …………………………………(3分)
…………………………………(3分)
(2)![]()
![]()
即当![]()
当![]() ………………………………………………(5分)
………………………………………………(5分)
(3)解不等式![]() ,对于函数
,对于函数![]()
若![]()
若![]()
![]()
同理可得,![]()
![]()
![]() ………………………………………………………(14分)
………………………………………………………(14分)