2005学年杭州市第一学期期末高一年级十二校联考数学问卷
考生须知：
1． 本卷满分100分，考试时间90分钟。
2． 答题前，在答卷密封区内填写学校、班级和姓名。
3． 所有答案必须写在答题卷上，写在试卷上无效。
4． 考试结束，只需上交答题卷。
一、选择题：本大题12小题，每小题3分，共36分，在每小题给出的四个选项中，有且只有一项是符合题目要求的。
1．指数函数y=ax的图像经过点（2,16）则a的值是
A．
B．
C．2 D．4
2．不等式(1–x) (2+x)<0的解集为
A．{x x>1} B．{x x<–2} C．{x x<–2或x>1} D．{x–2<x<1}
3．已知数列{an}中，a1=2, an+1–an=3(n≥1,n∈N)则数列{an}的通项an的表达式是
A．3n–1 B．3n–2 C．3n–5 D．
4．设集合M={x 0≤x<2}，集合N={x x2–2x–3<0}，则集合M∩N是
A．{x 0≤x<1} B．{x 0≤x<2} C．{x–1<x<3} D．{x–3<x<1}
5．已知映射f: A→B,其中集合A={–3,–2,–1, 1, 2, 3, 4},集合B中的元素都是A中元素在映射f下的像，且对任意的a∈A，在B中与它对应的元素是a, 则集合B是
A．{–3,–2, –1, 1, 2, 3, 4 } B．{1, 2, 3 } C．{1, 2, 3, 4 } D．{–1,–2,–3 }
6．设x∈R，则 x–2 <3是0<x<5的
A.充分而不必要条件 B．必要而不充分条件
C．充要条件 D．既不充分且不必要条件
7．设p, q是两个简单命题，下列命题中正确的是
A. P和非P可能同时成立
B．若p, q中只有一个真命题，则“p且q”为真命题
C．若p，q都为假命题，则“p或q”有可能为真命题
D．若p, q中只有一个真命题，则“p或q”为真命题
8．已知函数f(x)=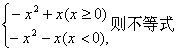
f(x)+2>0的解集是
A．(–2, 2) B．(–∞,–2) ∪(2, +∞) C．(–1, 1) D．(–∞,–1)∪(1,+∞)
9．已知
则f(x+1)等于
A．(x+1)2+2
B．x2+2 C．(x+1)2+
D．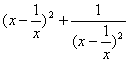
10．函数f(x)=
(6–x–x2)的单调递增区间是
A．
B．
C．
D．(–3, 
11．某厂去年产值为a,计划在5年内每年比上一年产值增长10%，从今年起5年内这个工厂的总产值是
A．1.14a B．1.15a C．10(1.15–1)a D．11(1.15–1)a
12．已知数列的通项公式an
，则数列{an}的前30项中最大值和最小值分别是
A．a10,a9 B．a10,a30 C．a1,a30 D．a1,a9
二、填空题：本大题有4小题，每小题3分，共12分，请将答案填写在答卷中的横线上。
13．在数列{an}中，首项a1=1,an=2an-1+1(n≥2,n∈N)，则a4=______________。
14．若点（1,2）既在函数y=
的图像上，又在它的反函数的图像上，则ab=______。
15．运载神舟五号飞船的长征四号火箭，在点火后1分钟通过的路程为1千米，以后每分钟通过的路程增加2千米，在到达离地面225千米的高度时，火箭与飞船分离，在这一过程中需要几分钟时间_______。
16．已知f(x)=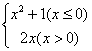 
若f(x)=10,则x=________________________。
三、解答题：本大题有5小题，共52分，解答应写出文字说明，证明过程或演算步骤。
17．（本小题满分10分）
已知R为全集，A=
B={x1<2x<16},求(1)A∪B; (2)A∩CRB.
18．（本小题满分10分）
已知在等比数列{an}中，a1+a2=2, a4+a5=16,求数列{an}的通项an与前n项和Sn.
19．（本小题满分10分）
已知函数f(x)=ax2+(a+2)x+b.
（1）若a=0,当–1<x<1时，f(x)>0恒成立，求实数b的取值范围;
（2）若f(0)=
,当x∈R时f(x)≥0恒成立，求函数g(a)=(a–4)(1+a–1)的值域.
20．（本小题满分10分）
已知数列{an}的前n项和为Sn,且满足a1=1，Sn–Sn–1= 2SnSn–1(n≥2).
（1）数列{
}是否为等差数列?请证明你的结论;
（2）求数列{an}的前n项和Sn.
21．（本小题满分12分）
集合A是由适合以下性质的函数f(x)组成的，对于任意的x≥0,f(x)∈
且f(x)在(0,+∞)上是增函数.
（1）试判断f1(x)=
及f2(x)=4–6×()x (x≥0)是否在集合A中，若不在集合A中，试说明理由；
（2）对于（1）中你认为是集合A中的函数f(x),不等式f(x)+f(x+2)<2f(x+1)是否对于任意x≥0总成立？试证明你的结论.
四、附加题：本题满分5分，计入总分，但全卷总分不超过100分.
已知数列{an}中,a1=1, a2n+1+an2+1
=2(an+1an+an+1–an)，求数列
的前n项和Sn.
2005学年杭州市第一学期期末高一年级十二校联考数学评分标准
一、选择题：本大题12小题，每小题3分，共36分，
在每小题给出的四个选项中，有且只有一项是符合题目要求的。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | C | A | B | C | B | D | A | A | B | D | A |
二、填空题：本大题有4小题，每小题3分，共12分，请将答案填写在答卷中的横线上。
13. 15 ; 14. –21 ;
15. 15 ; 16. –3或5 .
三、解答题：本大题有5小题，共52分，解答应写出文字说明，证明过程或演算步骤。
17．（本小题满分10分）
解：
……………………………2分
………………………………2分
………………………2分
………………………2分
……………………2分
18．（本小题满分10分）
解：
……………2分
又
……………2分
……………3分
………3分
19．（本小题满分10分）
（1）
时 
当
时 
恒成立
则
……………2分
得 
解得
……………1分
（2）若
……………1分
当时
不可能恒成立
当
时要使
恒成立，则 
……………2分
解得：
……………1分
……………1分
当
时
当
值域
……………2分
20．（本小题满分10分）
（1）
即
（常数）
为等差数列
……………5分
（2）
……………5分
21．（本小题满分12分）
（1）
不在集合A中
……………3分
又
的值域
，
当
时
为增函数（要证明）
在集合A中
……………3分
（2）
对任意，不等式
总成立 …6分
四、附加题：本题满分5分计入总分，但全卷总分不超过100分。
为等差数列
……………3分
=
=