等比数列的前n项和·例题解析

等比数列的前n项和·例题解析

 

【例1】　设等比数列的首项为a(a＞0)，公比为q(q＞0)，前n项和为80，其中最大的一项为54，又它的前2n项和为6560，求a和q．

解　由S_n=80，S_2n=6560，故q≠1

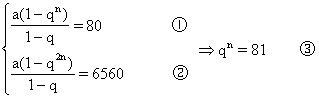
∵a＞0，q＞1，等比数列为递增数列，故前n项中最大项为a_n．

∴a_n=aq^n-1=54　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　④

将③代入①化简得a=q－1　　　　　　　　　　　　　　　　　　　　　　　　　　⑤

由⑤，⑥联立方程组解得a=2，q=3

证　∵S_n=a₁＋a₁q＋a₁q²＋…＋a₁q^n-1

S_2n=S_n＋(a₁qⁿ＋a₁qⁿ⁺¹＋…＋a₁q^2n-1)

=S_n＋qⁿ(a₁＋a₁q＋…＋a₁q^n-1)

=S_n＋qⁿS_n

=S_n(1＋qⁿ)

类似地，可得S_3n=S_n(1＋qⁿ＋q²ⁿ)

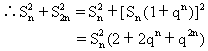
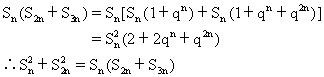
说明　本题直接运用前n项和公式去解，也很容易．上边的解法，灵活地处理了S_2n、S_3n与S_n的关系．介绍它的用意在于让读者体会利用结合律、提取公因式等方法将某些解析式变形经常是解决数学问题的关键，并且变得好，则解法巧．

【例3】　一个有穷的等比数列的首项为1，项数为偶数，其奇数项的和为85，偶数项的和为170，求这个数列的公比和项数．

分析　设等比数列为{a_n}，公比为q，取其奇数项或偶数项所成的数列仍然是等比数列，公比为q²，首项分别为a₁，a₁q．

解　设项数为2n(n∈N*)，因为a₁=1，由已知可得q≠1．

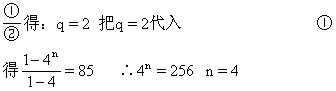
即公比为2，项数为8．

说明　运用等比数列前n项和公式进行运算、推理时，对公比q要分情况讨论．有关等比数列的问题所列出的方程(组)往往有高次与指数方程，可采用两式相除的方法达到降次的目的．

【例4】　选择题：在等比数列{a_n}中，已知对任意正整数n，有S_n=2ⁿ

[　]

解　D．

∵a₁=S₁=1，a_n=S_n－S_n-1=2^n-1

∴a_n=2^n-1

∴b_n=(a_n)²=(2^n-1)²=2^2n-2=4^n-1

【例5】　设0＜V＜1，m为正整数，求证：

(2m＋1)V^m(1－V)＜1－V^2m+1

分析　直接作，不好下手．变形：

右边分式的外形，使我们联想到等比数列求和公式，于是有：

(2m＋1)V^m＜1＋V＋V²＋…＋V^2m

发现左边有(2m＋1)个V^m，右边有(2m＋1)项，变形：V^m＋V^m＋…＋V^m＜1＋V＋V²＋…＋V^2m．

显然不能左右各取一项比较其大小，试用“二对二”法，即左边选两项与右边的两项相比较．鉴于左、右两边都具有“距首末等远的任意两项指数之和均相等”的特点，想到以如下方式比较：

V^m＋V^m＜1＋V^2m，V^m＋V^m＜V＋V^2m-1，…，V^m＋V^m＜V^m-1＋V^m+1，V^m=V^m．

即2V^m＜1＋V^2m，2V^m＜V＋V^2m-1，…．

根据“两个正数的算术平均值大于等于其几何平均值”，这些式子显然成立．

(具体证法从略)．

说明　本题最大的特点是解题过程中需要多次用到“逆向思考”：

C，B＜D，等等．善于进行逆向思考，是对知识熟练掌握的一种表现，同时也是一种重要的思维能力，平时应注意训练．

【例6】　数列{a_n}是等比数列，其中S_n=48，S_2n=60，求S_3n．

解法一　利用等比数列的前n项和公式

若q=1，则S_n=na₁，即na₁=48，2na₁=96≠60，所以q≠1

=S_n(1＋qⁿ＋q²ⁿ)

解法二　利用等比数列的性质：S_n，S_2n－S_n，S_3n－S_2n仍成等比数列

∴　(60－48)²=48·(S_3n－60)

∴　S_3n=63．

解法三　取特殊值法

取n=1，则S₁=a₁=48，S_2n=S₂=a₁＋a₂=60

∴　a₂=12

∵　{a_n}为等比数列

S_3n=S₃=a₁＋a₂＋a₃=63

【例7】　已知数列{a_n}中，S_n是它的前n项和，并且S_n+1=4a_n＋2(n∈N*)，a₁=1

(1)设b_n=a_n+1－2a_n(n∈N*)，求证：数列{b_n}是等比数列；

解　(1)∵　S_n+1=4a_n＋2

S_n+2=4a_n+1＋2

两式相减，得

S_n+2－S_n+1=4a_n+1=4a_n(n∈N*)

即：a_n+2=4a_n+1－4a_n

变形，得a_n+2－2a_n+1=2(a_n+1－2a_n)

∵　b_n=a_n+1－2a_n(n∈N*)

∴　b_n+1=2b_n</PGN0161A.TXT/PGN>

由此可知，数列{b_n}是公比为2的等比数列．

由S₂=a₁＋a₂=4a₁＋2，a₁=1

可得a₂=5，b₁=a₂－2a₁=3

∴　b_n=3·2^n-1

将b_n=3·2^n-1代入，得

</PGN0161B.TXT/PGN>

说明　利用题设的已知条件，通过合理的转换，将非等差、非等比数列转化为等差数列或等比数列来解决