任意的三角函数·基础练习题
一、选择题
1.下列说法正确的是 [ ]
A.小于90°的角是锐角
B.大于90°的角是钝角
C.0°~90°间的角一定是锐角
D.锐角一定是第一象限的角
答:D
解:0°~90°间的角指的是半闭区间0°≤θ<90°,小于90°的角可是以是负角或零角,大于 90°的角可以是任何象限的角.
2.设A={钝角},B={小于180°的角},C={第二象限的角}, D={小于180°而大于90°的角},则 下列等式中成立的是 [ ]
A.A=C
B.A=B
C.C=D
D.A=D
答:D
解:第二象限的角不是钝角,小于180°的角也不一定是钝角.
![]()
[ ]
A.第一象限角
B.第二象限角
C.第一象限角或第三象限角
D.第一象限角或第二象限角
答:C
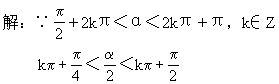
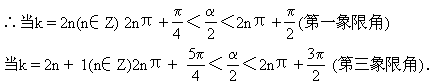
![]()
[ ]
A.重合
B.关于原点对称
C.关于x轴对称
D.关于y轴对称
答:C
解:∵α与-α角的终边关于x轴对称或重合于x轴上,θ=2kπ+
![]()
5.若α,β的终边互为反向延长线,则有 [ ]
A.α=-β
B.α=2kπ+β(k∈Z)
C.α=π+β
D.α=(2k+1)π+β(k∈Z)
答:D
解:在0~2π内α与β的终边互为反向延长线,则α=π+β或β=π+α,即α与π+β或α+π与β的终边相同,∴α=2kπ-(π+β)(k∈Z)或π+a=2kπ+β(k∈Z)∴α=2kπ-π+β(k∈Z)即α= (2k-1)π+β(k∈Z).

[ ]
A.A=B
![]()
D.以上都不对
答:A
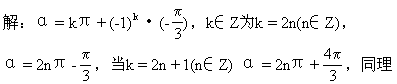


7.在直角坐标系中,若角α与角β的终边关于y轴对称,则α与β的关系一定是 [ ]
A.α+β=π
B.α+β=2kπ(k∈Z)
C.α+β=nπ(n∈Z)
D.α+β=(2k+1)π(k∈Z)
答:D
解:α与β的终边关于y轴对称,α+β的终边与π的终边相同∴α+β=2kπ+π=(2k+1)π(k∈Z).
8.终边在第一、三象限角的平分线上的角可表示为 [ ]
A.k·180°+45°(k∈Z)
B.k·180°±45°(k∈Z)
C.k·360°+45°(k∈Z)
D.以上结论都不对
答:A
解:∵终边在直线y=x(x>0)的角为α1=k·360°+45°(k∈Z)终边在直线y=x(x<0)上的角为α2=k·360°+225°(k∈Z)α1=2k·180°+45°,α2=2k·180°+180°+45°(k∈Z)α2=(2k+1)·180°+45°(k∈Z)
∴α=k·180°+45°(k∈Z).
9.一条弦的长等于半径,则这条弦所对的四周角的弧度数为 [ ]
![]()
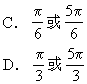
答:C

10.若1弧度的圆心角,所对的弦长等于2,则这圆心角所对的弧长等于 [ ]


答:C
解:∵1弧度的圆心角所对的弧长等于半径,设半径为R,R·
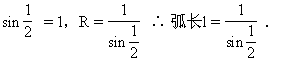
11.已知函数y=sinx·cosx·tgx>0,则x应是 [ ]
A.x∈R且x≠2kπ(k∈Z)
B.x∈R且x≠kπ(k∈Z)
![]()
D.以上都不对
答:C
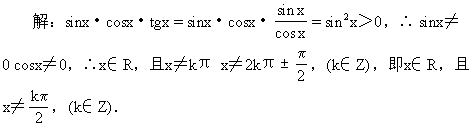

[ ]
A.0个
B.1个
C.2个
D.多于2个
答:C
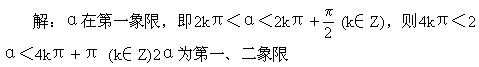
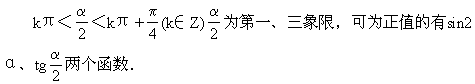
13.锐角α终边上一点A的坐标为(2sin3,-2cos3),则角α的弧度数为 [ ]
A.3
C.-3

答:D

14.在△ABC中,下列函数值中可以是负值的是 [ ]
A.sinA

D.tgA
答:D

![]()
终边上,则有
A.sinα<sinβ
B.sinα=sinβ
C.sinα>sinβ
D.以上皆非
答:B

![]()
[ ]
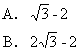

答:A
![]()
17.若tgθ+ctgθ=-2,则tgnθ+ctgnθ(n∈N)的值等于 [ ]
A.0
B.(-2)n
C.2(-1)n
D.-2(-1)n
答:C
![]()


18.已知:sinα+cosα=-1,则tgα+ctgα的值是
[ ]
A.2
B.-1
C.1
D.不存在
答:D
解:∵ sinα+cosα=-1,两边平方得1+2sinαcosα=1 ∴sinαcosα=0 sinα=0或cosα=0,∴tgα、ctgα不存在.

[ ]
A.0°<x<45°
B.135°<x<225°
C.45°<x<225°
D.0°≤x≤45°或135°≤x≤180°.
答:D
解:∵要使等式成立,cos2x≥0 ∴0°≤2x≤90°或270°≤2x<360° ∴ 0°≤x≤45°域135°≤x<180°.

[ ]
A.{α0<α<π}

答:A
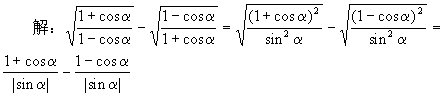


[ ]
A.0
B.-1
C.2
D.-2
答:D
![]()
![]()
[ ]
A.第一象限或第四象限
B.第二象限或第三象限
C.X轴上
D.Y轴上
答:D
![]()
![]()
23.在△ABC中,若sin2A=sin2B则该三角形为
[ ]
A.等腰三角形
B.等腰三角形或直角三角形
C.直三角形
D.等腰直角三角形
答:B
解:∵sin2A=sin2B,∴2A=2B,或2A=π-2B

24.若f(cosx)=cos2x,则f(sin15°)= [ ]
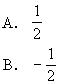

答:D
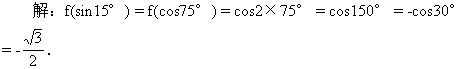
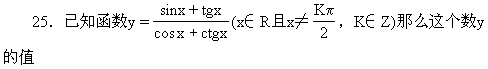
[ ]
A.等于零
B.小于零
C.大于零
D.可取任意实数值
答:C
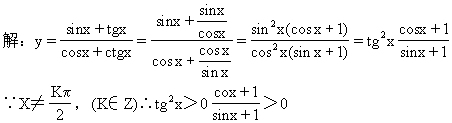
∴y>0.
![]()
[ ]

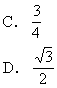
答:A
![]()

27.cos1°+cos2°+cos3°+…+cos179°+cos180°的值是
[ ]
A.0
B.1
C.-1
D.以上都不对
答:C
解:cos179°=cos(180°-1°)=-cos1.同理cos178°=-cos2°…
又∵cos90°=0,∴原式=cos180°=-1.
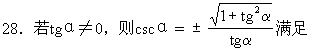
[ ]
A.当α在第一、四象限时,取“+”号
B.当α在第二、四象限时,取“-”号
C.当α在第一、二象限时,取“+”号
D.当α在第二象限时,取“+”号
答:A
解:∵当α在第一象限时cscα>0,tgα>0 ∴ 取“+”号,∵当α在第四象限时cscα<0,tgα<0,∴取“+”号.
![]()
[ ]
A.{-2,4}
B.{-2,0,4}
C.{-2,0,2,4}
D.{-4,-2,0,4}
答:B
解:∵x在第一象限时,y=4,x在第二象限时,y=-2,x在第三象限时y=0,x在第四象限时y=-2,∴值域是{-2,0,4}.
二、填空题
30.终边落在坐标轴上的角的集合是____
![]()
解:终边在x轴上的角为x=Kπ(K∈Z)终边在y轴上的角x=kπ+
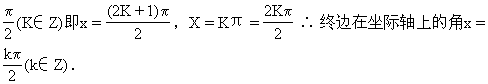
31.从5时到7时40分,分针旋转了____弧度,时针旋转了____弧度,如果分针长6cm,时针长4cm,分针比时针共走了____cm
![]()

32.一个扇形周长等于圆周长的一半,则扇形中心角的度数为____
![]()


![]()

34.自行车大链轮有48齿,小轮有20齿,当大链轮转过一周时,小轮转过角度是____度合____弧度.


![]()
![]()
答:(P-1)2
解:原式=p2+2p+1-4p=p2-2p+1=(p-1)2.

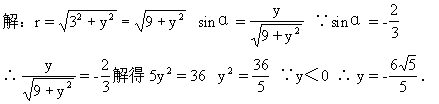
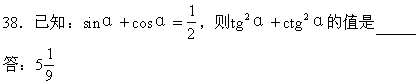



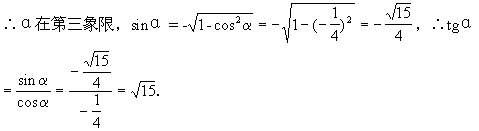
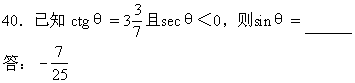

41.cos25°+cos215°+cos225°+cos235°+cos245°+cos255°+cos265°+cos275°+cos285=____
![]()
解:∵cos285°=sin25°,cos275°=sin215°,cos265°=
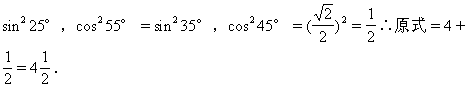
42.满足sinx=sin(-x)的x的范围是_____
答:2Kπ+π≤x≤2kπ+2π(k∈Z)
解:∵sinx=-sinx ∴ sinx≤0 2kπ+π≤x≤2kπ+2π(k∈Z).

![]()

44.在△ABC中,若tgA·tgB·tgC<0,那么这个三角形的形状是____
答:钝角三角形
解:∵A、B、C为三角形内角,tgA·tgB·tgC<0,可以得出tgA、tgB、tgC中有一个小于零,若tgA<0则A为钝角∴三角形为钝角三角形.
45.f(sinθ+cosθ)=sinθcosθ,则f(x)=____
![]()



三、解答题
46.写出与135°终边相同的角的集合,并从中求出终边位于-720°~720°之间的各角.
解:{αα=k360°+135°,k∈Z},α=k360°+135°中K=-2时,α=-585°,k=-1,α=-225°;k=0,
α=135°;k=1,α=495°.
47.一条弦的长度等于半径r,试求该弦与劣弧所组成的弓形的面积.

48.12点以后在什么时候,时针与分针第一次重合?什么时候分针第一次在时针的反向延长线上?
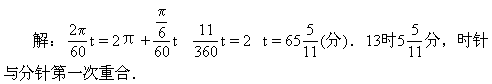


![]()
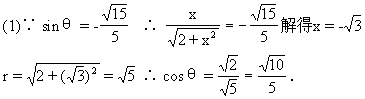

![]()

![]()

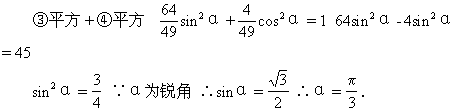
51.已知tg2α=2tg2β+1,求证:sin2β=2sin2α-1
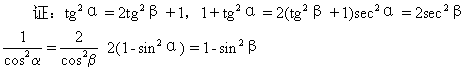
∴sin2β=2sin2α-1.
52.证明下列恒等式
![]()
证:(1)∵1-2csc2θ+cos4θ=(csc2θ-1)2=(ctg2θ)2=ctg4θ
∴1+csc4θ=2csc2θ+ctg4θ
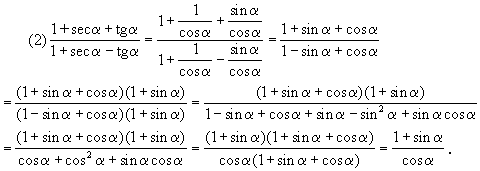
53.求证:csc6β-ctg6β=1+3csc2βctg2β
证:csc6β-ctg6β=(csc2β-ctg2β)(csc4β+csc2βctg2β+ctg4β)=csc4β-2csc2βctg2β+ctg4β+3csc2βctg2β
=(csc2β-ctg2β)2+3csc2βctg2β=1+3csc2βctg2β.
![]()

55.已知:sin2Acsc2B+cos2Acos2C=1,求证:tg2Actg2B=sin2C
证:sin2Acsc2B+cos2Acos2C=1
sin2A(ctg2B+1)=1-cos2Acos2C
sin2Actg2B+sin2A=sin2C+cos2C-cos2Acos2C
sin2Actg2B=sin2C+cos2C(1-cos2A)-sin2A
sin2Actg2B=sin2C+cos2Csin2A-sin2A
sin2Actg2B=sin2C+sin2A(cos2C-1)
sin2Actg2B=sin2C-sin2Asin2C sin2Actg2B=sin2Ccos2A
∴tg2Actg2B=sin2C.
![]()

![]()