西安中学2000-2001学年度第一学期期中考试
高二年级平面解析几何试题
命题人：陈昭亮
一、选择题（每小题4分，共40分）
1．若点P分
所成的比是
，则点B分
所成的比是（ ）
A．
B．
C．
D．
2．若A（-2，0），B（3，4），点P在线段AB的延长线上，且AP=2BP，则P的坐标为（ ）
A．
B．（8，8）
C．
D．以上答案都不对
3．若AB>0，AC>0，则直线Ax+By+C=0，不经过（ ）
A．第一象限 B．第二象限
C．第三象限 D．第四象限
4．点（a，b）关于直线x+y=0的对称点是（ ）
A．（-a，b） B．（a，-b）
C．（-a，-b） D．（-b，-a）
5．两条直线
和
垂直的充要条件是（ ）
A．
B．
C．
D．
6．已知直线
和
的夹角的平分线为直线y=x，如果的方程是ax+by+c=0（ab>0），那么的方程是（ ）
A．bx+ay+c=0 B．ax-by+c=0
C．bx+ay-c=0 D．bx-ay+c=0
7．下列四个命题中的真命题是（ ）
A．经过定点
的直线都可用
表示
B．经过任意两个不同的点
、
直线都可以用方程
表示
C．不经过原点的直线都可以用方程y=kx+b表示
D．经过定点A（0，b）的直线都可以用方程y=kx+b表示
8．直线2x-5y-10=0和两坐标轴所围成的三角形的面积是（ ）
A．10 B．5 C．2 D．1
9．若直线mx+10y=2和3x+（n-1）y=-1重合，则mn=（ ）
A．-10 B．-24 C．24 D．10
10．若两条直线：x+my+6=0和：（m-2）x+3y+2m=0平行，则m=（ ）
A．m=-1或m=3 B．m=1或m=-3
C．m=3 D．m=-1
二、填空题（每小题5分，共25分）
11．已知直线ax-y+2a=0和（2a-1）x+ay+a=0互相垂直，则a=_________。
12．不论m取何值，直线（2m-1）x+（m+3）y-（m-11）=0恒过定点，则这个定点的坐标是_____________。
13．设点P（x，y）在直线3x+4y-15=0上，则
的最小值是___________。
14．若动点A与两个定点B（0，0）、C（3，4）组成的三角形的面积为5，则动点A的轨迹方程是____________________。
15．已知两点P（-2，-2）、Q（1，3），直线和分别绕点P、Q旋转，且保持
则和的距离d的取值范围是_______________。
高二平面解析几何答题纸
一、选择题（每小题4分，共40分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题（每小题5分，共25分）
11．_____________ 12．____________
13．_____________ 14．____________
15．_____________
三、解答题（第16、17题每题12分，第18题11分，共35分）
16．求证：三点A（-2，12）、B（1，3）、C（4，-6）在同一直线上。（要求用二种或二种以上的方法给出证明）
17．直线L经过点A（1，2），且被直线3x+4y+1=0和3x+4y-4=0截得的线段长为
，求直线L的方程。
18．用解析法证明：等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高的长。（请完成下面的证明过程）。
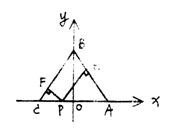
证明：建立如图所示的坐标系，设A（a，0），B（0，b），C（-a，0），（a>0；b>0），底边AB上任意一点为P（x，0）（-a≤x≤a）。
高二平面解析几何参考答案及评分标准
一、选择题（每小题4分，共40分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | B | C | D | A | A | B | B | C | D |
二、填空题（每小题5分，共25分）
11．a=0或1 12．（2，-3）
13．3 14．4x-3y±10=0
15．
三、解答题（共35分）
16．证法1：∵
∴
∴A、B、C三点在同一条直线上……6分
证法2：∵
∴AB+BC=AC
∴A、B、C三点在同一条直线上……12分
17．
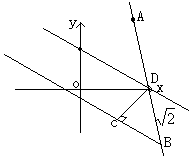
解：直线3x+4y+1=0和3x+4y-4=0
的距离
……2分
又∵
∴在Rt△DBC中，∠DBC=45°
即直线
和直线3x+4y+1=0的夹角为45°。……4分
设直线的斜率为k，则
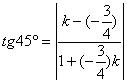……8分
解得
或-7；
∴的方程是
或y-2=-7（x-1）
即x-7y+13=0或7x+y-9=0……12分
18．证明：建立如图所示的坐标系，设A（a，0），B（0，b），C（-a，0）（a>0，b>0）。则直线AB的方程为bx+ay-ab=0，直线BC的方程为bx-ay+ab=0……2分
设底边AB上任意一点为P（x，0），（-a≤x≤a）。则
P到AB的距离为
……4分
P到BC的距离为
……6分
A到BC的距离为
……8分
∵
∴原命题得证。……11分