本章自测题
(一)选择题
①a∈M ②{a}
M ③a
M ④{a}∩M＝π，其中正确的是
[ ]
A．①② B．①④
C．②③ D．①②④
2．若A＝{1，3，x}，B＝{x2，1}，且A∪B＝{1，3，x}，则这样的x的不同值的个数是
[ ]
A．1个 B．2个
C．3个 D．4个
3．满足{x0＜x≤6，x为质数}
M{x0＜x≤6，x∈N*}的集合M的个数是
[ ]
A．4 B．5
C．7 D．8
4．下列四个命题中，不正确的命题是
[ ]
A．若A∩B＝
，则(CIA)∪(CIB)＝I
B．若A∩B＝，则A＝B＝
C．若A∪B＝I，则(CIA)∩(CIB)＝
D．若A∪B＝，则A＝B＝
5．有两个集合A、B，则A∩B＝A是A∪B＝B的
[ ]
A．充要条件
B．充分但不必要条件
C．必要但不充分条件
D．既不充分也不必要的条件
6．若集合M＝{x3x－1＜2}，N＝{xx2－3x＋2≤0}则M∪N等于
[ ]
A．{xx≥1} B．{xx≤2}
7．二次函数y＝－3x2＋kx＋k＋1的图像与x轴没有交点，则k的取值范围是
[ ]
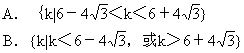
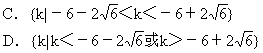
8．由下列各组命题构成的复合命题中，“p或q为真”、“p且q为假”、“非p”为真的是
[ ]
A．p：0＝，q：0∈
B．p：等腰三角形都是锐角三角形
q：正三角形都相似
C．p：CV＝U，q：CVU＝
D．p：不等式x＞x的解集是x＜0
q：不等式x≤x的解集是
9．不等式x＋1＋x＋2＜5的所有实数解地集合是
[ ]
A．{x－3＜x＜2}
B．{x－1＜x＜3}
C．{x－4＜x＜1}
10．若x－2＜a时，不等式x2－4＜1成立，则正数a的取值范围是
[ ]
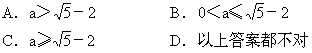
(二)填空题
1．设I＝{a，b，c，d，e，f，g，h}，已知①CIA∪CIB＝{a，b，c，e，f，g，h}；②CIA∩B＝{c，g}；③CIB∩A＝{b，h}；则A＝________，B＝________．
2．设全集I＝{2，4，a2－a＋1}，A＝{a＋1，2}，CIA＝{7}，则实数a＝________．
3．若A＝{xx2＋3x－10＜0}，B＝{xx＜3}，全集I＝R，则A∪CIB＝________．
4．若不等式x2－ax－b＜0的解集为{x2＜x＜3}，则不等式bx2－ax－1＞0的解集为________．
5．若不等式x2－(2a＋1)x＋a2＋a＜0的解集为A，x2－5x＋4≥0的解集为B，且AB，则a的取值范围是________．
6．“不等式ax2＋bx＋c＞0的解集是R”的充要条件是________．
(三)解答题
1．解下列不等式：
(2)x2＋2＞3x
2．设I＝R，A＝{xx＞1}，B＝{xx2＋4x＋3＜0}，求集合C，使其同时满足下列条件：
(1)C(CIA∪B)∩Z
(2)C有两个元素
(3)C∩B≠
3．集合A＝{xx2－3x＋2＝0}，B＝{xx2－ax＋a－1＝0}，C＝{xx2－mx＋2＝0}．已知A∪B＝A，A∩C＝C．
求a，m的值及集合B、C．
A∩B＝B，求实数a的取值范围．
证明：(1)若2∈A，则集合A中必还有另外两个元素；
(2)集合A不可能是单元素集；
(3)集合A中至少有三个不同的元素．
参考答案
(一)选择题
合与集合之间的关系，③元素a与集合M应该是属于关系而不是包含关系，④集合{a}与M的交集应该是一个集合而不是一个元素π，所以③、④都不正确．
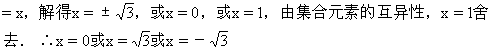
5，6}的集合M的个数，即求{1，4，6}的真子集个数，得23－1=7
4．B
7．C 依题意，Δ＜0，即k2－4x(－3)·(k＋1)＜0，解得－6
8．B
9．C
方法一：零点分段法．当x≤－2时，原不等式化为－x－1－x－2＜5，解得x＞－4；当－2＜x≤1时，原不等式化为－x－1＋x＋2＜5解得1＜5(恒成立)；当x＞1时，原不等式化为x＋1＋x＋2＜5，解得x＜1，∴原不等式的解集为{x－4＜x＜1}．
方法二：图像法，由绝对值不等式的几何意义，原题即求数轴上到点－1和到点－2的距离之和小于5的点的集合．
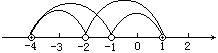
先找出到点－1和到点－2距离之和等于5的两个点－4和1，则由题意－4和1之间的点都满足条件，即到点－1和到点－2的距离之和小于5的点的集合为{x－4＜x＜1}．
10．B 设不等式x－2＜a的解集为A，不等式x2－4＜1的解
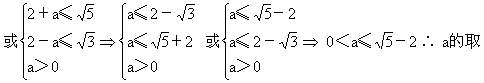
(二)填空题
1．{b，d，h}，{c，d，g}．用文恩图表示集合I，A，B的关系，如图所示的有关区域表示集合CIA∪CIB、CIA∩B、CIB∩A，并填上相应的元素，可得A={b，d，h}，B={c，d，g}．
2．3 依题意，a2－a＋1=7，解得a=－2或a=3．当a=－2时，
3．{xx＜2或x≥3}．解不等式得A={x－5＜x＜2}，CIB={xx≥3}={xx≥3或x≤－3}，∴A∪CIB={xx＜2或x≥3}
5．a≤0或a≥4 解不等式得A={xa＜x＜a＋1}，B={xx≥4
6．a＞0且b2－4ac＜0或a=b=0且c＞0．
(三)解答题
{x－5＜x＜2或3＜x＜7}．
等式组：
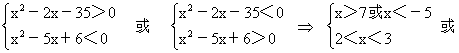
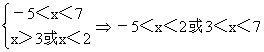
解(三)：就分母大于0或小于0，把分式不等式转化成整式不等式．x2－5x＋6＞0时，41－3x＞x2－5x＋6或x2－5x＋6＜0时，41－3x＜x2－5x＋6，以下步骤同解二．
(2)解(一)平方法
∴原不等式的解集为{xx＜－2或－1＜x＜1或x＞2}
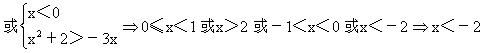
或－1＜x＜1或x＞2．
解(四)图像法：在同一坐标系分别作出y=x2＋2和y=3x的图像．
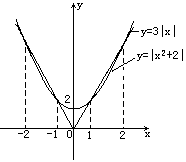
求出方程x2＋2=3x的根x1=1，x2=2，x3=－1，x4=－2．由图像及其要点求出不等式的解：x＜－2或－1＜x＜1或x＞2．
2．化简集合A、B得A={xx＞1 或x＜－1}，B={x－3＜x＜－1}， ∴(CIA∪B)∩Z={x－3＜x≤1，x∈Z}={－2，－1，0，
个元素，∴集合C为{－2，－1}或{－2，0}或{－2，1}．
3．化商集合A、B 得A={1，2}，B={x(x－1)[x－(a－1)]=0}={1，
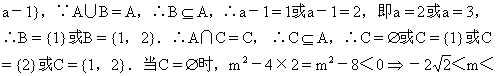
={1，2}矛盾．∴C≠{1}．同理C≠{2}．当C={1，2}时，m=3，∴
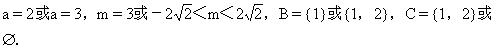
4．化简集合A、B，得A={x1≤x＜3}，B={x(x－a)(x－1)≤
是1≤a＜3．
=－8＜0，∴4x2＋6x＋3＞0恒成立．∴2x2＋(6－2k)x＋(3－k)＞0．∵不等式的解集为R，a=2＞0，∴Δ＜0．即(6－2k)2－4×2(3－k)＜0，(k－3)2＋2(k－3)＜0，∴1＜k＜3．
解(二)：∵分母中a=4＞0，Δ＜0，∴4x2＋6x＋3x＞0恒成立，∴原不等式可化为 2x2＋2kx＋k＜4x2＋6x＋3．整理得2x2＋(6－2k)x＋3－k＞0，以下步骤同解(一)．
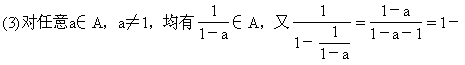
元素