本章自测题(一)
(一)选择题
1.设函数f(x)=x2(-1<x≤1),那么它是
[ ]
A.偶函数
B.既奇又偶函数
C.奇函数
D.非奇非偶函数
2.下列各组函数中,表示同一函数的是
[ ]
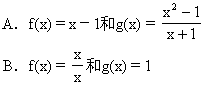
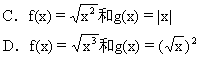
3.对于x∈(0,1)的所有值,函数f(x)=x2与其反函数f-1(x)的相应函数值之间一定成立的不等式是
[ ]
A.f(x)<f-1(x)
B.f(x)≥f-1(x)
C.f(x)=f-1(x)
D.f(x)≤f-1(x)
4.y=f(x)是定义在R上的偶函数,则下列坐标所表示的点在y=f(x)的图像上的是
[ ]
A.(a,-f(a))
B.(-a,f(a))
C.(-a,-f(-a))
D.(-a,-f(a))</PGN0086B.TXT/PGN>
5.已知y=f(x)是奇函数,当x>0时,f(x)=x(1+x),当x<0时,f(x)等于
[ ]
A.-x(1-x) B.x(1-x)
C.-x(1+x) D.x(1+x)
6.已知y=-x2+2在[0,+∞)上的反函数是y=f-1(x),则f-1(1)的值是
[ ]
A.1 B.-1
![]()
7.若f(x)=x2-2x+2(x≤1),g(x)是f(x)的反函数,则g(x)是
[ ]
A.在(-∞,1]上递增的偶函数
B.在(-∞,1]上递增的奇函数
C.在[1,+∞)上递减的偶函数
D.在[1,+∞)上递减的非奇非偶函数
![]()
[ ]
A.[0,1] B.[1,2]
C.[-1,1] D.[0,2]
9.函数f(x)(x∈R)为偶函数,且f(x)在[0,+∞)上是增函数,则f(-2)、f(-π)、f(3)的大小顺序是
[ ]
A.f(-π)>f(3)>f(-2)
B.f(-π)>f(-2)>f(3)
C.f(-π)<f(3)<f(-2)
D.f(-π)<f(-2)<f(3)
![]()
[ ]
A.是增函数
B.是减函数
C.既是增函数又是减函数
D.没有单调性
(二)填空题
1.已知函数f(x)=3x+b-2是奇函数,那么常数b________.
![]()
3.函数y=2(x2-2x)+3在区间[0,3]上的最大值是________,最小值是________.
![]()
5.已知二次函数f(x)满足f(x+1)-f(x)=2x,且f(0)=1,则f(x)的表达式是________.
6.已知f(x)是奇函数,g(x)是偶函数,且f(x)-g(x)=x2+3x+2,则f(x)+g(x)=________.</PGN0087A.TXT/PGN>
(三)解答题
![]()
2.讨论y=ax3的单调性,并证明你的结论.
3.设f(x)是定义在实数集R上的偶函数,且在(-∞,0)上是减函数,又f(2a2+a+1)>f(3a2-2a+1),求a的取值范围.
![]()
求a、b、c的值.
参考答案
(一)选择题
1.(D).解:已知函数y=x2的定义域不关于原点对称,∴它是非奇非偶函数.
2.(C).(1)解:(A)中,f(x)的定义域是R,g(x)的定义域是x≠-1,两者定义域不同,是不同函数.(B)中f(x)的定义域是x≠0,g(x)的定义域是R.两者是不同函数.(D)中f(x)的定义域是R,g(x)的定义域是x≥0,两者是不同函数.(C)中,两者定义同,对应法则也同.是相同函数.
3.(A).解作出函数y=x2及其反函数f-1(x)在x∈(0,2)内的图像.由图像易得f-1(x)>f(x).
4.(B).解:∵x=a时,y=f(a),∴(A)中点(a,-f(a))是错的.当x=-a时,y=f(-a)又∵f(-a)=f(a),∴(B)中的点(-a,f(a))是对的,而(C)、(D)是错的.
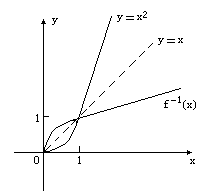
5.(B).解:当x<0时,f(x)=-f(-x)=-(-x)[1+(-x)]=x(1-x).选(B).
6.(A).解法(一):函数y=-x2+2,x≥0的值域为y≤2,其
![]()
解法(二):由-x2+2=1,得x=±1,∵x≥0,∴舍x=-1,故x=1,因此f-1(1)=1.
7.(D).解:∵f(x)=(x-1)2+1(x≤1),则f(x)值域为[1,+∞),且f(x)在(-∞,1]上是递减函数,故g(x)在[1,+∞)上是递减函数且定义域不关于原点对称,是非奇非偶函数.
![]()
9.(A).解:∵f(-x)=f(x),且在[0,+∞)上为增函数,又π>3>2>0,∴f(π)>f(3)>f(2),即f(-π)>f(3)>f(-2).
10.(D).</PGN0201A.TXT/PGN>
(二)填空题
1.2.解:∵f(x)为奇函数的充要条件是b-2=0,∴b=2.
![]()
3.9,1.解y=2(x-1)2+1,x∈[0,3].而1∈[0,3],∴当x=3时,ymax=9,当x=1时,ymin=1.
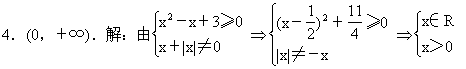
∴函数的定义域为(0,+∞).
5.y=x2-x+1.
6.-x2+3x-2.解:f(x)-g(x)=x2+3x+2 ①,-f(x)-g(x)=x2-3x+2 ②,①+②得g(x)=-x2-2,①-②得f(x)=3x.
(三)解答题
1.解:由-x2+x+2≥0,得定义域为[-1,2].令u(x)=-x2
![]()
![]()
![]()
![]()
a>0时,f(x1)<f(x2),y在R上为增函数,当a=0时,y为常数函数,当a<0时,f(x1)>f(x2),y在R上为减函数.
3.解:∵f(x)是R上的偶函数,又f(x)在(0,+∞)上是增函数.∵
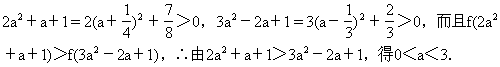
![]()