集合·基础练习
(一)选择题
1.下列命题正确的是
[ ]
A.1是集合N中最小的数.
B.x2-4x+4=0的解集为{2,2}
C.{0}不是空集
D.太湖中的鱼所组成的集合是无限集
2.下列各条件
(1)大于5小于20且既能被3整除也能被2整除的数的全体;
(2)方程x2+2x+7=0的解的全体;
(3)某学校校园内部的柳树的全体;
(4)大于50的无理数的全体;
其中能确定一个集合的有________个.
| A.1个 | B.2个 |
| C.3个 | D.4个 |
3.已知集合A={yy=-x2+5x-4,x∈R},则有
[ ]
A.1∈A,且4∈A

(二)填空题
1.已知集合A={x∈Rax2+2x+1=0,a∈R},若A中元素至多只有一个,则a的取值范围是________.
2.实数集{3,x,x2-2x}中的元素x应满足的条件为________.
3.已知x、y、z∈R,且x、y、z都不为0,则M=
![]()
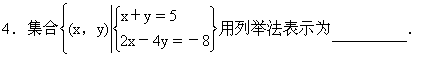
5.设A={xx=2k,k∈Z},B={xx=2k+1,k∈Z},C={xx=4k+1,k∈Z},又若a∈A,b∈B,则a+b∈________(填A、B、C之一).
(三)解答题
1.用两种方式写出下列各题解的集合.

2.设f(x)=x2+ax+b,A={xf(x)=x}={a},求a、b的值.
3.已知小于或等于x的最大整数与大于或等于x的最小整数之和是7,求x的集合.
![]()
ab∈A.
参考答案
(一)选择题
1.C((A)中N包含元素0.(B)不满足集合元素互异性.(D)太湖中鱼是有限的而不是无穷多的)
2.D(注意(B)中x2+2x+7=0的解集是空集,(C)学校校园内部的树是确定的.)
3.B(集合A是二次函数y=-x2+5x-4中,y的取值范围,而不是一元二次方程-x2+5x-4=0的解集,而y=-x2+5x-4=-(x
![]()
(二)填空题
1.a≥1或a=0 ①当ax2+2x+1=0是一元二次方程时,即a≠0时,Δ=4-4a≤0,∴ a≥1
②当a=0时,ax2+2x+1=0是一元一次方程2x+1=0也有一个根,因此也满足条件.
2.x≠-1且x≠0且x≠3(由集合元素的互异性知,
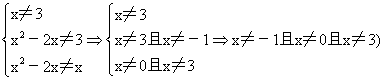
3.3个 ①当x,y,z都是正数时m=4 ②当x,y,z都是负数时m=-4 ③当x,y,z有两个正数一个负数或两个负数一个正数时m=0)
4.(2,3)
5.B(A={xx=2k,k∈z}={偶数} B={奇数} C集合为所有被4整除余1的数,∵ a为偶数,b为奇数,∴ a+b为奇数故a+b∈B)
(三)解答题</PGN0176A.TXT/PGN>

②{xx2-1=0}={1,-1}
③{x(x-1)2=0}={1}
![]()
![]()
b=0,∵ A={a}∴ 方程x2+(a-1)x+b=0有两个相等实根为a,∴ 将a代入方程得:a2+a(a-1)+b=0①又由Δ=0得(a-1)2-4b=0② 解
![]()
3.{x∈R3<x<4} ①当x是整数时:x+x=7 x=3.5∈Z,舍去.②当x不是整数时,设n<x<n+1,</PGN0176B.TXT/PGN>n∈Z,∴ n+(n+1)=7,∴ n=3 ∴ 3<x<4,∴ {x∈R3<x<4})
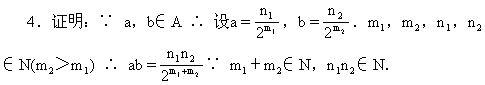
∴ ab∈A