江苏省清江中学2005--2006学年度期中考试
高 一 数 学
时间:120分钟 满分:150分 命题人：袁金飞
一．选择题：(有且只有一个正确答案)
1．设集合A=
，a=
,那么……………………………………（ ）
A） a
A B） a
A C） {a}∈A D）
{a}A
2．若集合S=
,T=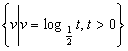
,则S∩T=………( )
A）φ B） T C） S D） 有限集
3．如右图矩形表示集合S，则阴影部分表示的集合是…………………（ ）
A）
B）
C）
D）
4．已知a>0,a≠1,m,n∈R，下列各式中正确的是（ ）
A） 
B） 
C）
(m,n>0) D） 
5．函数y=f(x)的值域为[a,b]，则y=f(x-1)的值域为（ ）
A） [a,b] B） [a-1,b-1] C） [a+1,b+1] D） [-b,-a]
6．下列函数既不是奇函数，又不是偶函数的是（ ）
A） y=
B） y=
C） 
D） 
7．已知集合A={x0≤x≤4},集合B={x0≤x≤2}，下列由A到B的对应：
①f：x→y=
，②f：x→y=
，③f：x→y=
，④f：x→y=x-2。
其中能构成映射的是（ ）
A）①② B） ①③ C） ③④ D） ②④
8．函数
的定义域是（
）
A）
≤x<2 B） <x≤2 C） <x<2或x>2 D） 2≤x≤3
9．已知a=0.32，b=log20.3，c=20.3，则a,b,c之间的大小关系是（ ）
A） a<c<b B） a<b<c C） b<c<a D） b<a<c
10．已知镭经过100年剩留后原来质量的95.76%，则质量为1的镭经过的年数x与剩留量y之间的函数关系式是( )
A）
B） 
C） 
D） 
11．函数y=
的递增区间是（ ）
A） (-∞,0) B） (1,2) C） (0,1) D） (2,+∞)
12．根据表格中的数据，可以判定方程ex-x-2=0的一个根所在的区间为（ ）
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
A） (-1,0) B） (0,1) C） (1,2) D） (2,3)
二、填空题：
13．高一某班有学生45人，其中参加数学竞赛的有32人，参加物理竞赛的有28人，另有5人两项竞赛都不参加，则该班既参加数学竞赛又参加物理竞赛的人数为 。
14．已知幂函数y=f(x)的图象过点(2,
)，则f(9)=
。
15．已知方程x2-ax+a-1=0的一个根大于0，另一个根小于-2，则实数a的取值范围是 。
16．函数f(x)=lg(ax2-2x+1)的值域为R，则实数a的取值范围为 。
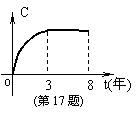17．某工厂八年来某产品总产量C与时间t(年)的函数关系如图所示，下列四种说法：(1) 前三年中产量增长的速度越来越快；
(2) 前三年中产量增长的速度越来越慢；
(3) 第三年后，这种产品停止生产了；
(4) 第三年后，年产量保持不变；
(5) 函数C是(0,8)上的增函数。
其中正确的说法是 。
江苏省清江中学2005--2006学年度期中考试
高 一 数 学 答 题 纸
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题：
13． ；14． ；15． ；16． ；17． .
三、解答题：
18．已知集合A=
，B={x2<x<10}，C={xx<a}，全集为实数集R.
(1) 求A∪B，(CRA)∩B；(2)如果A∩C≠φ，求a的取值范围。
| |
| |
20．指数函数
的图象如图所示，
①在已知图象的基础上画出指数函数
的图象(说明理由)；
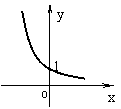②求y=ax2+bx+1的顶点的横坐标的取值范围。
 |
21．已知函数f(x)=
。
(1)求函数f(x)的定义域；(2)判断函数f(x)的奇偶性；(3)求证：f(x)>0
| |
22．探究函数
,x∈(0,+∞)的最小值，并确定相应的x的值，列表如下：
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
请观察表中y值随x值变化的特点，完成下列问题：
(1)若函数,(x>0)在区间(0,2)上递减，则在
上递增；
(2)当x= 时，,(x>0)的最小值为
；
(3)试用定义证明,(x>0)在区间(0,2)上递减；
(4)函数,(x<0)有最值吗？是最大值还是最小值？此时x为何值？
解题说明：(1)(2)两题的结果直接填写在横线上；(4)题直接回答，不需证明。
| |
第(3)题的解题过程如下：
| |
第(4)题的答案为：
23．已知函数
,
(1)当a=1时，求f(x)的最大值与最小值；
(2)求实数a的取值范围，使函数f(x)在[-2,2]上是减函数；
(3)求函数f(x)的最大值g(a)，并求g(a)的最小值。
| |