江苏省大丰市高级中学
高一第二次阶段性考试试题(普通、强化班)
一、选择题（本大题共12小题，每小题5分，共60分）
1、四棱台由（ ）条棱组成.
A 4 B 8 C 12 D 16
2、设
满足
，下列不等式中正确的是( )
A 
B 
C 
D
3、已知x满足方程
，则x的值是（ ）
A 1 B 2 C 1，2 D -1，2
4、函数y=5-2x（x≤0）的值域是( )
A （-∞，5） B [4，5) C （0，5] D [4，5]
5、已知集合A={
} B={
}则A
=（ ）
A
R
B {
}
C {
}
D {
}
6、 定义全集U={xx是丰中学生}，集合A={xx是丰中初中部学生}，B={xx是丰中女生}，则集合{xx是丰中高中部女生}可以表示为( )
A 
B 
C 
D 
7、已知点A(a,b)是函数y=2x与函数y=21-x图象的交点，则a落在下列（ ）区间内。
A （3，4） B （4，5） C （5，6） D （6，7）
8、已知关于x的方程
有两个负根，则
的取值范围是（ ）
A 
B
C 
D 
9、有五名运动员的某队派队员参加一项比赛，人数不限，队中两名优秀队员必定参加，则有（ ）种不同的安排方案
A 5 B 6 C 7 D 8
10、(普通班做)定义差集A-B={xx∈A,且x
B},现有三个集合A、B、C分别用圆表示，则集合C-(A-B)可表示下列（ ）图中的阴影部分。
A
B
C 
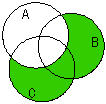D
（强化班做）已知集合A={1，2，3，4}，B={2，4，6，8}，定义集合A×B={(x, y) x∈A，y∈B}，则集合A×B中有（ ）个元素属于集合{(x, y) logxy∈N}。
A 4 B 5 C 8 D 9
11、设
是定义在
上的一个增函数，
，那么
为( )
A 增函数且是奇函数 B 增函数且是偶函数
C 减函数且是奇函数 D 减函数且是偶函数
12、已知函数
，现有
，则
=（ ）
A
2 B -2 C 
D 
二、填空题：（本大题共6小题，每小题4分，共24分）
13、立体几体中，三视图指______________________________三种视图.
14、函数
的定义域是
_____________.
15、计算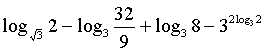
=_______________________.
16、已知函数
，0<x1<x2，则
________
.
（用”>”、”<”、”=”、”≥”或”≤”填空）
17、已知函数
，则
________.
18、(普通班做)已知
是方程
的一个根，则的近似值是_____________(精确到0.1).
（强化班做）用二分法求方程
在区间(-0.8,0)内的根是_________（精确到0.1）.
三、解答题（12+12+14+14+14）
19、已知二次函数满足
，
，（1）求f(1), f(2)的值；
(2) 求函数f(x)的解析式。
20、已知函数
（1）求
的值；
（2）计算：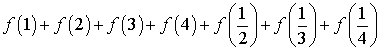
21、已知偶函数y=f(x)定义域是[-3，3]，当x≤0时，f(x)=-x2-2x.
（1）写出函数y=f(x)的解析式； （2）求函数y=f(x)的值域；
（3）写出函数y=f(x)的单调递增区间。
22、（普通班做）某供水供应公司的蓄水池有水450吨，公司每小时可向蓄水池注水80吨，同时蓄水池又向居民小区供水，
小时内供水量
吨，现在开始向池中注水并同时向居民小区供水.
（1）多少小时后蓄水池中水量最少？
（2）若蓄水池中水量少于150吨时，就会出现供水紧张现象，问每天有几个小时供水紧张？
(强化班做) 某商店按每件80元的价格，购进时令商品（卖不出去的商品将成为废品）1000件；市场调研推知：当每件售价为100元时，恰好全部售完；当售价每提高1元时，销售量就减少5件；为获得最大利润，商店决定提高售价x元，获得总利润y元。
（1）请将y表示为x的函数；
（2）确定合理的售价，并求出此时的利润。
23、某饮料公司经市场调研，发现该饮料的日销售额（y万元）与天气气温（x℃）之间有密切联系。现知，当气温分别为25℃、27℃、29℃时，日销售额分别为1万元、1.1万元、1.3万元。为了调节生产，需估测气温升高后对日销售额的影响，以这三个气温下的日销售额为依据，用一个函数模拟日销售额（y万元）与天气气温（x℃）关系。模拟函数考虑选用二次函数
或函数
（其中
为常数）。现已知气温为33℃时，该饮料的日销售额为2.2万元， 请问用以上哪个函数作为模拟函数较好，并说明理由。
答案：
1-6 C C B B B C 7-12 B D D A A D
13、 主视图，俯视图，左视图 14、 (1,2]
15、 -2 16、 <
17、 0 18、（普通班）1.6 （强化班）-0.3
19、(1) f(1)=1;f(2)=3; (2) f(x)=x2-x+1.
20、（1）由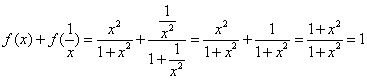
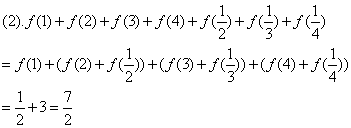
21、 (1)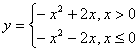 
(2) y∈[-3,1] (3) 递增区间[-3,-1],[0,1]
22、（普通班做）(1)
=
当t=5时,ymin=50. 所以,5小时后,池水量最小.
(2) <150
得
,所以
,从而,每天有10个小时供水紧张.
(强化班做)设比100元的售价高
元，总利润为
元；则
显然，当
即售价定为150元时，利润最大；其最大利润为32500元；
23、模拟函数为
和
当x=33时，y1=2, y2=2.5与日销售额2.2相比，显然二次函数模拟更好一点。