宜兴市张渚高级中学第二次调研考试－数学试卷

宜兴市张渚高级中学高一数学第二次调研考试

命题人：何兴伟

一、选择题：（本题共12小题，每题5分，满分60分）

1、如果平面a外一条直线 l 与a内的两条直线垂直，那么l与a的位置关系是(　)

A．l⊥a　　B．l∥a　　　 C．l与a斜　　D．不能确定

2、M＝｛正四棱柱｝，N＝｛长方体｝，Q＝｛正方体｝，P＝｛直四棱柱｝．则下列关系中正确的是 　　　　　　　　　　　　　 　　（　　 ）

A、QMNP　 　B、QMNP 　 　C、QNMP 　　 D、QNMP

3、下列四个命题中，假命题是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A．若平面 a 内有两条相交直线与平面 b 内的两条相交直线分别平行，则a∥b

B．平行于同一平面的两个平面平行

C．如果平面 a 内有无数条直线都与平面 b 平行，则a∥b

D．如果平面a 内任意一条直线都与平面 b 平行，则a∥b

4、

A．c与a、b都不相交　　　　　　　　　　　　　　　　B．c与a、b都必相交

C．c至少与a、b的一条相交　　 　　　　D．c至多与a、b的一条相交

5、如图，已知AA₁与BB₁是异面直线，且AA₁=2，BB₁=1，AB⊥BB₁，A₁B₁⊥BB₁，则AA₁与BB₁所成的角为　　 （　　 ）　　　　　　　　　 

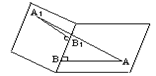
A.30°　　　　　　B.60°　　C.45°　　　　　　　　D.90°

6、若函数的图象过两点(-1，0)和(0，1)，则 (　　 )　　　

A．a = 2,b = 2　B．a = ,b = 2　 C．a = 2,b = 1　  D．a = ,b =

7、已知函数的图象是连续的,有如下的x, 的对应值表:

x	1	2	3	4	5	6
	36.36	15.52	－3.92	10.88	－2.48	－32.6

 则函数存在零点的区间有 (　　 )

A.　 区间[1, 2]和[2, 3]　　　　　　　  B.　　区间[2, 3]和[3, 4]

C.  区间[2, 3] , [3, 4] , [4, 5]　　　　　  D.　 区间[3, 4], [4, 5]和[5, 6]

8、函数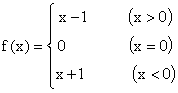,  则的值是(　　  )

A.　　1　　　B.　  　　 C.　  　　 D.　　 

9、已知函数为偶函数, 则在(－5，－2)上是(　　 )

A.　 增函数 　　　　　　　　B.　 减函数　

C.　 非单调函数 　　　　　　D.　 可能是增函数,也可能是减函数

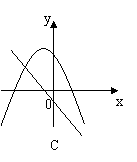
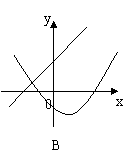
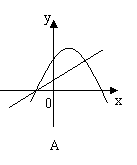
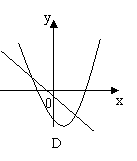10、一次函数与二次函数在同一坐标系中的图象大致是(　　)

11、若函数是定义在R上的偶函数，在上是减函数，且，则使得的x的取值范围是(　　 )　　　　　　　　　　　　　　　　　　　

A．　　　　B．　　　　C．　 D．（－2，2）

12、如果圆台的上底面半径为5，下底面半径为R，中截面把圆台分为上、下两个圆台，它们的侧面积的比为1：2，那么R=（　　）

A．10　　 　　　B.15　　　　　 C.20　　　　　　　D.25

二、填空题（本题共4小题，每题4分，满分16分）

13、函数y=的定义域为_____________。

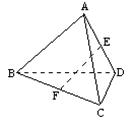14、在三棱锥A－BCD中，平面ABD⊥平面BCD，∠BDC＝90°，E、F分别是AD、BC的中点，若EF＝CD，则EF与平面ABD所成的角为___________．

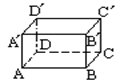
15、已知长方体ABCD-A'B'C'D'中棱AA'=5，AB=12，那么直线B'C'与平面A'BCD'的距离为_________．

16、经过（2，4）且在两坐标轴上的截距相等的直线方程为___________.

宜兴市张渚高级中学高一数学第二次调研考试

一、选择题：（本题共12小题，每题5分，满分60分）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	D	B	C	C	B	A	C	C	A	C	D	D

二、填空题（本题共4小题，每题4分，满分16分）

13、_____________________　　 14、________30⁰___________________

15、_______________________　　　16、y=2x或x+y-6=0___________________

三、解答题（本题共6小题，满分74分）

17、为上的奇函数，当时，，求的解析式.

18、若0≤x≤2,求函数y=的最大值和最小值；

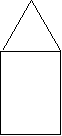
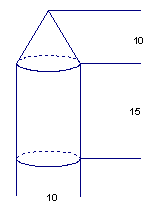
19、下面是某物体的三视图，试根据观察完成问题。

1）　画出物体的直观图；　　　　　　　　  10

2）　根据数据求出该物体的表面积和体积。

　　　　　　　　　　　　　　　　　　　 15

　　　　　　  　　　　　　　　　　　　　　10

20、已知函数f(x)是定义在(-5,5)上的奇函数又是减函数，试解关于x的不等式

f(3x-2)+f(2x+1)>0

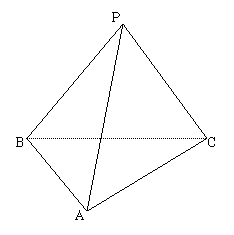21、已知：如图，△ABC中，AB=6cm，AC=8cm，BC=10cm，P是平面ABC外一点，且PA=PB=PC=6cm．

(1) 平面ABC⊥平面ＰBC

(２)求点P到平面ABC的距离；

(３)求PA与平面ABC所成角的余弦．

22、直三棱柱中ABC-A₁B₁C₁中,B₁C₁=A₁C₁,AC₁⊥A₁B,M,N分别为A₁B₁,AB中点，求证：

1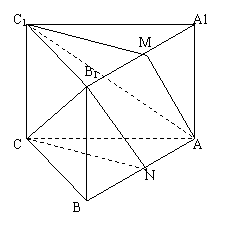）　平面AMC₁∥平面NB₁C

2）　C₁M⊥平面AB B₁A₁

3）　A₁B⊥AM

三．解答题．

17．解：当时，，则

　　　　　　　为奇函数，

　　　　　　　，

　　　　　　　，

综上：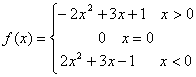

18．解：

　　　　　　　令，则

　　　　　　　则

　　　　　　　，

19．解：１）

２）．

　　　

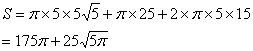
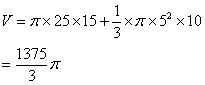
20．解：由题意得：

又为奇函数，，则

则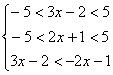　　　　　　

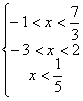
21．证明：１）取BC中点D

PA=PB=PCP在平面ABC中的射影为ABC的外心

由AB=6,BC=10,AC=8　 得ABC为直角三角形,且ABAC

则D为ABC的外心,故PD平面ABC

又PＤ平面PBC, 平面PBC平面ABC

　　　　　　　　２）由１知PD平面ABC，故ＰＤ即为Ｐ到平面ABC

的距离　ＰＤ＝

　　　　　　　　３）连接AD,则AD＝５

由PD平面ABC　　知即为PA与平面ABC所成的角

22．证明：１）连接MN

Ｍ,N为中点MNABN,四边形M AN为平行四边形,

 四边形M NB为平行四边形N//MA, BMN

N//平面ＭＡ，ＭＮＣ四边形ＣＭＮ为平行四边形，

Ｍ//CN,  CN//平面ＭＡ,  CNN=N

平面ＭＡ//平面CN

　　　　　　　　2）Ａ面得ＡＭ

　　　　　　　　　　 ＝，Ｍ为中点得Ｍ

故Ｍ面

　　　　　　　　3）由2知Ｍ,又

得面ＭA AM