|
学校_________________班级______________姓名_____________考号______________座位号________________ |
2005-2006学年度高一数学月考试卷2005.12.17
测试时间:100分钟,满分:150分
一、选择题(12×5=60分)
1.方程![]() 的解集是( )
的解集是( )
(A) {3} (B) {-1} (C) {-1,3} (D) {1,3}
2.下列说法中正确的是( )
(A)三点确定一个平面.
(B)两条直线确定一个平面.
(C)三条直线两两相交,则这三条直线共面.
(D)空间四点中如果有三点共线,则这四点共面.
3.给出下列命题:
(1) 同垂直于一直线的两直线平行.
(2) 同平行于一平面的两直线平行.
(3) 同平行于一直线的两直线平行.
(4) 平面内不相交的两直线平行.
其中正确的命题个数是( )
(A) 1 (B) 2 (C) 3 (D) 4
4.若![]() ={异面直线所成角};
={异面直线所成角};
![]() ={斜线与平面所成角};
={斜线与平面所成角};
![]() ={直线与平面所成角},则有 ( )
={直线与平面所成角},则有 ( )
(A)
![]() (B)
(B)
![]()
(C)
![]() (D)
(D)
![]()
5.直线![]() ,
,![]() ‖
‖![]() ,则
,则
![]() 与
与![]() 的关系为( )
的关系为( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
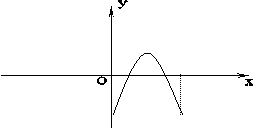
6.偶函数f(x)的定义域[-5,5],其在[0,5]的图象如下所示,则![]() >0的解集为( )
>0的解集为( )
 (A) {x2<x<4}
(A) {x2<x<4}
(B) {x![]() <4}
<4}
(C) {x-4<x<-2}
(D){x2<x<4或-4<x<-2} 2 4 5
7.函数![]() =
=![]() 为( )
为( )
(A)是奇函数但不是偶函数 (B)是偶函数但不是奇函数
(C)既是奇函数又是偶函数 (D)既不是奇函数又不是偶函数
8.两条异面直线在同一平面的正投影不可能是( )
(A)两条平行直线 (B)两条相交直线
(C)一个点和一条直线 (D)两个点
9.设![]() 是正方体
是正方体 ![]() 的一条对角线,则这个正方体中面对角线与
的一条对角线,则这个正方体中面对角线与![]() 异面的有( )
异面的有( )
(A)0条 (B)4条 (C)6条 (D)12条
10.方程
![]() =
=![]() 实数解的个数为( )
实数解的个数为( )
(A)1 (B)2 (C)3 (D)4
11.![]() =
=![]() +
+![]() +
+![]() 的图象的对称轴是
的图象的对称轴是![]() =2,则有( )
=2,则有( )
(A)![]() <
<![]() <
<![]() (B)
(B)![]() <
<![]() <
<![]()
(C) ![]() <
<![]() <
<![]() (D)
(D)![]() <
<![]() <
<![]()
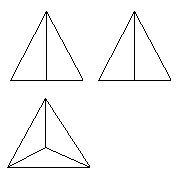
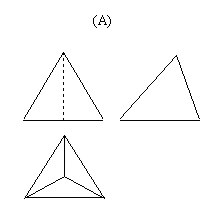
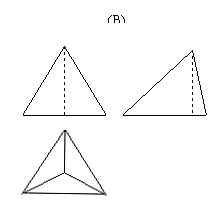
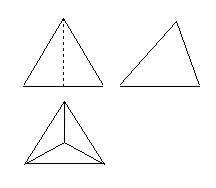
12.如图是正三棱锥(底面边为4,高为4),则它的三视图是( )

![]()

 |  | ||||||||
| |||||||||
| |||||||||
 | |||||||||
学校_________________班级______________姓名_____________考号______________座位号________________ |
2005-2006学年度高一数学月考试卷2005.12.17
测试时间:100分钟,满分:150分
答题纸
一选择题(12×5=60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 答案 | A | D | B | B | C | D |
| 7 | 8 | 9 | 10 | 11 | 12 | |
| B | D | C | C | B | C |
二填空(6×4=24分)
13.已知![]() =
= ![]() ,则
,则 ![]() =_____4_________
=_____4_________
14.用”<”从小到大排列![]() 、
、![]() 、
、![]() 、
、![]()
__________![]() <_
<_![]() <_
<_![]() _<_
_<_![]() ____________________________
____________________________
15.一球的表面积与它的体积的数量相等,则球的半径为______3_____________
16.直线a、b分别是长方体相邻两个面上的对角线所在直线,则a与b的位置关系为______相交或异面______
17.空间四边形![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() =3、
=3、![]() =4、
=4、![]() =
=![]() ,那么
,那么![]() 与
与![]() 所成角的度数是____90度______
所成角的度数是____90度______
18.长方体的长、宽、高之比是1:2:3,对角线长是![]() ,则长方体的体积是_____48______
,则长方体的体积是_____48______
三.解答题(19、20、21每题10分,22、23、24每题12分)
19.已知全集![]() ={
={![]() },
}, ![]() ={
={![]() },
},![]() ={
={![]() }
}
求![]() 、
、![]() 、
、![]()
解:![]() ={x1<x<2}
={x1<x<2}
![]() ={xx<3}
={xx<3}
![]() ={x2≤x<3}
={x2≤x<3}
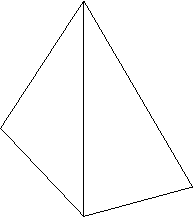
20.已知四面体![]() 的棱长都相等
的棱长都相等
求证:![]()
证明:取CD的中点E,连结AE、BE
则AE⊥CD,BE⊥CD从而有CD⊥面ABE∴AB⊥CD
 A
A
 |
B
|
C
21.在三棱锥![]() 中,
中,![]() 、
、![]() 分别为△ABC和△BCD的重心
分别为△ABC和△BCD的重心
求证:![]() ‖
‖![]()
|
|
|
|
|
|

证明:连结AM、AN,并延长交BC、CD于E、F,连结EF、MN
∵M、N为重心∴AM:ME=AN:NF=2:1
∴MN‖EF
又E、F分别为中点,则有EF为中位线∴EF‖BD故![]() ‖
‖![]()
22.已知![]() 是正方体,
是正方体,
求:
|
|
|
|

![]()
![]() (2)求
(2)求![]() 与平面
与平面![]() 所成的角(45°)
所成的角(45°)
|
|
23. 如图,已知四棱锥![]() 的侧面是正三角形,
的侧面是正三角形, ![]() 是
是![]() 的中点
的中点
求证:(1)![]() ‖
‖![]()
|
|
|
|
|
|
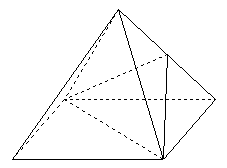
证明:(1)连结AC交BD于0点,连结EO
则O为AC的中点,则有OE为中位线∴OE‖AP
∴![]() ‖
‖![]()
(2)在△BCP中,有BE⊥PC
在△DCP中,有DE⊥PC又DE∩BE=E故有PC⊥面BDE
又PC在平面PAC上
∴平面BDE ![]() 平面PAC
平面PAC
24 .某厂生产某种零件,每只的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定每次订购超过100个时,每多订一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元
(1)当一次订购多少个时,零件的实际出厂单价恰好降为51元?
(2)设一次订购量为![]() 个,零件的实际出厂单价为P元,写出函数
个,零件的实际出厂单价为P元,写出函数
![]() 的表达式.
的表达式.
解:(1)设订购了x个,则有(x-100)×0.02=60-51
解得x=550
(2)
![]() 60
0<X≤100
60
0<X≤100
P= 60—(x-100)×0.02 100<x≤550 (x∈N)
51 x≥550