高2008第一学期期末数学模拟试卷(二)
一、选择题(本大题共12小题,每小题5分,共60分)
1、已知集合![]() ( )
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
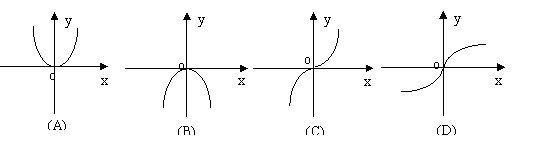 2、函数
2、函数 ![]() 的图像大致是( )
的图像大致是( )
3、在等差数列![]() 中,若它的前n项之和
中,若它的前n项之和![]() 有最大值,且
有最大值,且![]() ,那么当
,那么当![]() 是最小正数时,n的值为( )
是最小正数时,n的值为( )
A、1 B、18 C、19 D、20
4、设原命题“若p则q”真而逆命题假时,则p是q的( )
A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
5、已知集合![]() ,集合
,集合![]() 。映射
。映射![]() .那么这样的映射
.那么这样的映射![]() 有( )个.
有( )个.
A、0 B、2 C、3 D、4
6、已知数列![]() 的前n项和
的前n项和![]() =
=![]() ,则此数列的奇数项的前n项和是( )
,则此数列的奇数项的前n项和是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7、如果![]() 的两个根为
的两个根为![]() ,那么
,那么![]() 的值为( )
的值为( )
A、lg2+lg3 B、lg2lg3
C、![]() D、-6
D、-6
8、在等差数列![]() 中,已知
中,已知![]() 的值为( )
的值为( )
A、30 B、20 C、15 D、10
9、已知![]() 的图像与函数
的图像与函数![]() 的图像关于直线y=x对称,
的图像关于直线y=x对称,
则![]() 的值为( )
的值为( )
A、11 B、12 C、2 D、4
10、若函数![]() 的定义域为[0 , m],值域为
的定义域为[0 , m],值域为![]() ,则m的取值范围是( )
,则m的取值范围是( )
A、(0 , 4] B、![]() C、
C、![]() D、
D、![]()
11、互不相等的四个负数a、b、c、d成等比数列,则![]() 与
与![]() 的大小关系是( )
的大小关系是( )
A、![]() >
>![]() B、
B、![]() <
<![]() C、
C、![]() =
=![]() D、无法确定
D、无法确定
12、已知等差数列![]() 中,
中,![]() ( )
( )
A、42 B、22 C、21 D、11
二、填空题(本大题共4小题,每小题4分,共16分)
13、数列![]() 的前n项和
的前n项和![]() ,则其通项公式为
.
,则其通项公式为
.
14、函数![]() 的定义域为
.
的定义域为
.
15、国家规定个人稿费纳税办法为:不超过800元的不纳税;超过800元而不超过4000元的按800元的14%纳税;超过4000元的按全稿酬的11.2%纳税。某人出版了一书共纳税420元,这个人的稿费为 元。
![]() 16、黑白两种颜色的正六边形地面砖按如图
16、黑白两种颜色的正六边形地面砖按如图
的规律拼成若干个图案:
则第n个图案中有白色地面砖 块。
三、解答题(本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤)
17、(本小题满分12分)已知R为全集,A=![]() , B =
, B =![]() ,
,
求![]() .
.
18、(本小题满分12分)已知函数![]() 在区间[—
在区间[—![]() ,0]上有
,0]上有![]() ,试求a、b的值。
,试求a、b的值。
19、(本小题满分12分)在等比数列![]() 中,前n项和为
中,前n项和为![]() ,若
,若![]() 成等差数列,则
成等差数列,则![]() 成等差数列。(1)写出这个命题的逆命题;(2)判断逆命题是否为真,并给出证明。
成等差数列。(1)写出这个命题的逆命题;(2)判断逆命题是否为真,并给出证明。
20、(本小题满分12分)某公司实行股份制,一投资人年初入股a万元,年利率为25%,由于某种需要,从第二年起此投资人每年年初要从公司取出x万元。
(1)分别写出第一年年底,第二年年底,第三年年底此投资人在该公司中的资产本利和。
(2)写出第n年年底此投资人的本利之和![]() 与n的关系式(不必证明);
与n的关系式(不必证明);
(3)为实现第20年年底此投资人的本利和对于原始投资a万元恰好翻两番的目标,若a=395,则x的值应为多少?(在计算中可使用lg2=0.3)
21、(本小题满分12分)已知函数![]() 。(1)求函数
。(1)求函数![]() 的定义域;(2)若函数
的定义域;(2)若函数![]() 在[10,+∞]上单调递增,求k的取值范围。
在[10,+∞]上单调递增,求k的取值范围。
22、
本小题满分14分)已知函数![]() 的解析式为
的解析式为![]() =
=![]() (x<-2)。(1)求
(x<-2)。(1)求![]() 的反函数
的反函数![]() ;(2)设
;(2)设![]() ,证明:数列
,证明:数列![]() 是等差数列,并求
是等差数列,并求![]() ;(3)设
;(3)设![]() ,是否存在最小正整数m ,使得对任意
,是否存在最小正整数m ,使得对任意![]() 成立?若存在,求出m的值;若不存在,说明理由。
成立?若存在,求出m的值;若不存在,说明理由。
参考答案
一、1.B;2.C;3.C;4.A;5.D;6.C;7.C;8.A;9.D;10.C;11.B;12.D
二、13.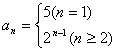 ;14.
;14.![]() ;15.3800;16.4n+2.
;15.3800;16.4n+2.
三、17. ![]()
18.(1)![]() 或
或 ![]()
19.(1)逆命题:在等比数列![]() 中,前n项的和为
中,前n项的和为![]() ,若
,若![]() 成等差数列,则
成等差数列,则![]() 成等差数列;(2)当
成等差数列;(2)当![]() 时,逆命题为假;当
时,逆命题为假;当![]() 时,逆命题为真。
时,逆命题为真。
20.(1)第一年年底本利和:![]() ,第二年年底本利和:
,第二年年底本利和:![]() ,第三年年底本利和:
,第三年年底本利和:![]() ;(2) 第n年年底本利和:
;(2) 第n年年底本利和:![]()
![]()
![]() ;(3)
;(3)![]()
21.(1)当![]() 时,定义域为
时,定义域为![]() ,当
,当![]() 时,定义域为
时,定义域为![]() 当
当![]() 时,定义域为
时,定义域为![]() ;(2)
;(2)![]()
22.(1)![]() ;(2)
;(2)![]() ;(3)m=6
;(3)m=6