高一数学第二学期期终考试卷(2008.6)
| 题次 | 一 1-12 | 二 13-20 | 21 | 22 | 23 | 24 | 总分 |
| 得分 |
|
|
|
|
|
|
|
本卷满分120分,考试时间90分钟
一.填空题:(本题满分48分,每小题4分)
1.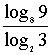 的值为
的值为
2.已知函数![]() 的图象过点(1,7),又知其反函数的图象经过点(4,0),则
的图象过点(1,7),又知其反函数的图象经过点(4,0),则![]() 的表达式为
的表达式为
3.函数 的定义域为
的定义域为
4.若![]() 则
则![]()
5.若![]() 则
则![]() 的值是
的值是
6.在![]() 中,
中,![]() ,则
,则![]() =
=
7.把![]() 化成
化成![]() 的形式:
的形式:
8.![]() =
=
9.函数![]() 的最小正周期是
的最小正周期是
10.函数![]() 的单调递增区间是
的单调递增区间是
11.函数![]() 的值域是
的值域是
12.![]() 的解集是
的解集是
二.选择题:(本题满分32分,每小题4分)
13.已知![]() ,那么
,那么![]() 角终边的位置在
( )
角终边的位置在
( )
(A) 第二象限或第三象限
(B) 第三象限或第四象限
(C) 第二象限或第三象限或x轴负半轴
(D) 第一象限或第四象限或x轴正半轴
14.函数![]() 是( )
是( )
(A)周期为![]() 的奇函数 (B)周期为
的奇函数 (B)周期为![]() 的偶函数
的偶函数
(C)周期为![]() 的奇函数 (D)周期为
的奇函数 (D)周期为![]() 的偶函数
的偶函数
15.在![]() 中,若
中,若![]() 则三角形的形状是
( )
则三角形的形状是
( )
(A) 等腰三角形 (B)直角三角形
(C)等腰或直角三角形 (D)等腰直角三角形
16.已知![]() 则
则![]() 的值是( )
的值是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
17.函数![]() 的图象的一条对称轴是
( )
的图象的一条对称轴是
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
18.函数![]() 的最大值是
( )
的最大值是
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
19.要得到函数![]() 的图象,只要将函数
的图象,只要将函数![]() 的图象 ( )
的图象 ( )
(A)左平移![]() (B)右平移
(B)右平移![]() (C) 左平移
(C) 左平移![]() (D) 右平移
(D) 右平移![]()
20.已知![]() ,则x的取值范围是
( )
,则x的取值范围是
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
三.解答题:(共40分)
21.(本题满分8分)已知![]() ,
,
求: ![]()
22.(本题满分10分)已知函数![]()
(1)求函数![]() 的定义域
的定义域
(2)判断![]() 的奇偶性并证明
的奇偶性并证明
(3)求![]() 的反函数
的反函数![]()
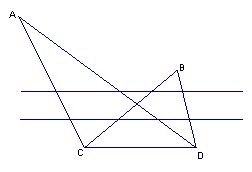 23.(本题满分10分)隔河看到两目标A,B,但不能到达,在河边选取相距
23.(本题满分10分)隔河看到两目标A,B,但不能到达,在河边选取相距![]() 千米的C,D两点,并测得
千米的C,D两点,并测得![]() 在同一平面内),求两个目标A,B之间的距离。
在同一平面内),求两个目标A,B之间的距离。
24.(本题满分12分)一根细线上端固定,另一端系一个小球,小球来回摆动时,离开平衡位置的位移![]() 和时间
和时间![]() (秒)的函数关系是
(秒)的函数关系是![]() 求:
求:
(1)小球在摆动过程中,离开平衡位置最大距离是多少?
(2)小球来回摆动一次需要多少时间?
(3)当![]() 秒时,小球离开平衡位置的距离是多少?
秒时,小球离开平衡位置的距离是多少?
(4)画出小球开始摆动后位移时间图象。
2007学年度高一数学第二学期期终考答案
一.填空题:
1.![]() 2.
2.![]() 3.
3.![]() 4.
4.![]() 5.
5.![]() 6.7 7.
6.7 7.![]()
8.![]() 9.1 10.
9.1 10.![]() 11.
11.![]() 12.
12.![]()
二.选择题:
13.D 14.A 15.C 16.A 17.A 18.C 19.B 20.D
三.解答题:
21.![]()
![]()
![]() ,且
,且![]()
![]()
即![]()
22.(1)![]() ,即定义域为(-1,1)
,即定义域为(-1,1)
(2)任取![]()
![]() ,
,![]()
![]()
![]() 是奇函数
是奇函数
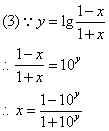 即
即![]()
23.![]() 中,
中,![]()
![]()
![]() 中,
中,![]()
![]()
![]() 中,
中,![]()
即两个目标AB间的距离为![]() 千米.
千米.
24.(1)![]() 函数的振幅是4
函数的振幅是4 ![]() 小球在摆动过程中离开平衡位置最大距离是4
小球在摆动过程中离开平衡位置最大距离是4![]()
(2)![]() 周期
周期![]()
![]() 小球来回摆动一次需要2秒
小球来回摆动一次需要2秒
(3)当![]() 时,
时,![]()
即离开平衡位置距离为![]()
(4)
