高一数学第二章函数测试题
一、选择题：（本题共12小题，每小题3分，共36分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1、若
，且
为整数，则下列各式中正确的是
（ ）
A、
B、
C、
D、
2、已知函数
（ ）
A．b B．－b C．
D．－
3、.若集合M={yy=2—x}, P={yy=
}, M∩P=
（ ）
A．{yy>1} B．{yy≥1} C．{yy>0 } D．{yy≥0}
4、由于电子技术的飞速发展，计算机的成本不断降低,若每隔5年计算机的价格降低
，则现在价格为8100元的计算机经 年后降为2400元.
（ ）
A．14 B．15 C．16 D．17
5、函数
的值域为
（ ）
A、
B、
C、
D、
6、设
，则
（ ）
A、
B、
C、
D、
7、在
中，实数
的取值范围是
（ ）
A、
B、
C、
D、
8、有以下四个结论 1 lg(lg10)=0 2 lg(lne)=0 3若10=lgx,则x=10 4 若e=lnx,则x=e2, 其中正确的是 （ ）
A.13 B.24 C.12 D. 34
9、已知函数f(x)=2x,则f(1－x)的图象为 （ ）
 |  |  |  | ||||
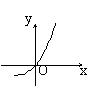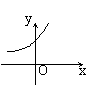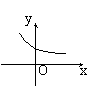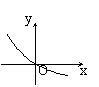A B C D
10、已知f(x)是偶函数,它在[0,+∞)上是减函数,若
,则x的取值范围是( )
A. 
B.
C.
D.(0,1)∪(10,+∞)
11、世界人口已超过56亿,若按千分之一的年增长率计算,则两年增长的人口就可相当于一个 ( )
A.新加坡(270万) B.香港(560万) C.瑞士(700万) D.上海(1200万)
12、若函数
在区间
上的最大值是最小值的3倍，则的值为 （ ）
A、
B、
C、
D、
二、填空题：（本题共4小题，每小题4分，共16分，请把答案填写在答题纸上）
13、
-lg25-2lg2
___________
____；
14、
(a>0且a≠1),a的取值范围为
;
15、已知函数f(x)=log 2(x-2)的值域是[1，log 214],那么函数f(x)的定义域是 ；
16、设0≤x≤2,则函数
的最大值是________,最小值是______.
高一数学函数第一单测试答题卡
班次________学号__________姓名_____________得分______________
一、选择题(每题4分,共48分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题(每题4分,共16分)
13. ；14. ；15. ；16. 、 .
三、解答题：（本题共5小题，共48分，解答应写出文字说明，证明过程或演算步骤.）
17、(10分)已知f(x)=log a
(a>0, 且a≠1）
⑴求f(x)的定义域
⑵求使 f(x)<0的x的取值范围.
18. (8分)某电器公司生产A型电脑,1993年这种电脑每台平均生产成本为5000元,并以纯利润20%确定出厂价.从1994年开始,公司通过更新设备与加强管理.使生产成本逐年降低.到1997年,尽管A型电脑出厂价是1993年的80%,但却实现了50%纯利润的高效益.
(1) 求1997年每台A型电脑的生产成本;
(2) 以1993年的生产成本为基数,求从1993年至1997年生产成本平均每年降低的百分数(精确度0.01，以下数据可供参考:
19、(10分)若
是定义在
上的增函数，且
(1)求
的值；(2)若
，解不等式
．
20．(10分)已知函数f(x2-3)=lg
(1)求f(x)表达式及定义域 ；（2）判断函数f(x)的奇偶性.
21任选作一题．（10分)
⑴函数f(x)=loga(x－3),当点P（x,y)是函数y=f(x)图象上的点时，Q（x－2,－y)是函数y=g(x)图象上的点.
①写出函数y=g(x)的解析式.
②若f(x)>g(x),求x的取值范围.
⑵函数ƒ(x)=a
+4x-3,当x∈[0,2]时在x=2取得最大值,求a的取值.