2008届高三文科数学第二轮复习资料
——《平面向量和三角函数》专题
1. 证明: 
．
2. 已知函数
.
（1）若
，求函数
的值；
（2）求函数的值域；
（3）画出函数在区间
上的图象.
3. 在△ABC中，角A、B、C所对的边分别是a、b、c，若
，且
，求△ABC的面积．
4. 观察以下等式：
分析上述各式的共同特点，写出能反映一般规律的等式，并对等式的正确性作出证明．
5. 已知圆内接四边形ABCD的边长分别为AB=2，BC=6，CD=DA=4，求四边形ABCD的面积
6. 已知函数
.
（I）写出函数
的最小正周期和单调递增区间；
（II）若函数的图象关于直线
对称，且
，求
的值．
7．已知函数
的定义域为
，值域为[ －5，1 ]，求常
数a、b的值．
8. 设关于x的函数y=2cos2x－2acosx－(2a+1)的最小值为f(a)，试确定满足f(a)=
的a值，并对此时
的a值求y的最大值
9. 已知A、B、C是
的三个内角，a，b，c为其对应边，向量
（Ⅰ）求角A；
（Ⅱ）若
10. 是否存在实数a，使得函数y=sin2x+a·cosx+
a－
在闭区间［0，
］上的最大值是1？若存在，求出对应的a值；若不存在，试说明理由.
11.已知某海滨浴场海浪的高度y(米)是时间t
的函数,记作
,下表是某日各时的浪高数据:
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
经过长期观察,y=f(x)的曲线可近似地看成是函数
（1）以t为横坐标,y为纵坐标在直角坐标系中画出表中数据的散点图;
（2）根据以上数据,求函数的最小正周期T,振幅A及函数表达式;
（3）依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8:00时至晚上20:00时之间,有多少时间可供冲浪者进行运动?
12. 海岛上有一座高出水面1000米的山，山顶上设有观察站A，上午11时测得一轮船在A的北偏东60°的B处，俯角是30°，11时10分，该船位于A的北偏西60°的C处，俯角为60°，
（1）求该船的速度；
（2）若船的速度与方向不变，则船何时能到达A的正西方向，此时船离A的水平距离是多少？
（3）若船的速度与方向不变，何时它到A站的距离最近？
|
参考答案
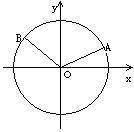
1. 证明：如图：在单位圆上任取两点A、B，设以OX为始边，OA、OB为终边的角分别为
∴
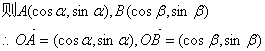
又
∴
2.解：（1）
，
.
（2）
，
，
，
， 
函数的值域为
.
(3) 图略
3.解：由已知得b2+c2=a2+bc，
，
由
，
4.解:上述各式的共同特点是:一个角的正弦的平方与比这个角大30°的角的余弦的平方和再加上这两个角的正弦与余弦的乘积等于同一个常数3/4．即：
证明：左边=
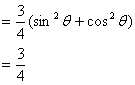
5. 
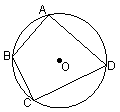解
如图 连结BD，则有四边形ABCD的面积
S=S△ABD+S△CDB=·AB·ADsinA+·BC·CD·sinC
∵A+C=180°，∴sinA=sinC
故S=(AB·AD+BC·CD)sinA=(2×4+6×4)sinA=16sinA
由余弦定理，在△ABD中，BD2=AB2+AD2－2AB·AD·cosA=20－16cosA．
在△CDB中，BD2=CB2+CD2－2CB·CD·cosC=52－48cosC，∴20－16cosA=52－48cosC，
∵cosC=－cosA，∴64cosA=－32，cosA=－，
又0°＜A＜180°，∴A=120°，故S=16sin120°=8
6.解：（I）
由
，得 
的单调递增区间为
（II）
的图象关于直线对称，
7．解： 
，
．
∵ 
，∴ 
，
∴ 
．
当a > 0时，b ≤ f ( x ) ≤ 3a + b，
∴ 
解得 
当a < 0时，3a + b ≤ f ( x ) ≤ b ．
∴ 
解得 
故a、b的值为 
或 
8.解
由y=2(cosx－
)2－
及cosx∈［－1，1］得
f(a)＝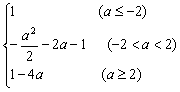
∵f(a)=,∴1－4a=
a=
［2,+∞
或 －
－2a－1=，解得a=－1
，
此时，y=2(cosx+)2+，当cosx=1时，即x=2kπ，k∈Z，ymax=5
9. 解:（Ⅰ）
，
，
，
，
（Ⅱ）
由正弦定理，得
即
.
、C为的内角，
又
为正三角形．
又
10.
综合上述知，存在
符合题设.
11.解: (1) 图略
(2) 由表中数据可知:周期T=12，
由t=0,y=1.5得A+b=1.5；由t=3,y=1.0得b=1.0．解得:A=0.5,b=1，
所以,振幅A=1/2, 
(3) 由题意::y>1时海滨浴场才对冲浪者开放，
，
，
．
所以,在上午8:00至晚上20:00之间有6个小时可供冲浪者运动,即上午9:00至下午5:00.
12.
|
，
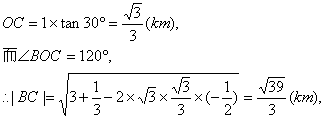
∴船的速度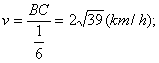
（2）设船到达的正西位置为D（x，0），
∵B的坐标为
而C的坐标为
∵B、C、D三点共线，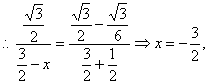
，
该船在上午11时15分到达正西方向；
（3）作OE⊥BC于E，则E点到A的距离最近，
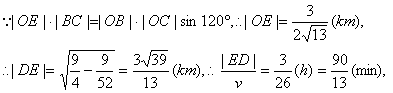
船在上午11时
分时到A的距离最近.