2008届高三文科数学第二轮复习资料
——《应用题》专题
高考应用性问题的热门话题是增减比率型和方案优化型， 另外，估测计算型和信息迁移型也时有出现.当然，数学高考应用性问题关注当前国内外的政治，经济，文化， 紧扣时代的主旋律，凸显了学科综合的特色.
1．解应用题的一般思路可表示如下
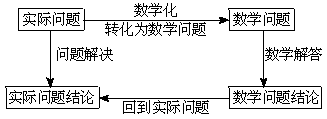
2．解应用题的一般程序
（1）读：阅读理解文字表达的题意，分清条件和结论，理顺数量关系，这一关是基础.
（2）建：将文字语言转化为数学语言，利用数学知识，建立相应的数学模型.熟悉基本数学模型，正确进行建“模”是关键的一关.
（3）解：求解数学模型，得到数学结论.一要充分注意数学模型中元素的实际意义，更要注意巧思妙作，优化过程.
（4）答：将数学结论还原给实际问题的结果.
3．中学数学中常见应用问题与数学模型
（1）优化问题.实际问题中的“优选”“控制”等问题，常需建立“不等式模型”和“线性规划”问题解决.
（2）预测问题：经济计划、市场预测这类问题通常设计成“数列模型”来解决.
（3）最（极）值问题：工农业生产、建设及实际生活中的极限问题常设计成“函数模型”，转化为求函数的最值.
（4）等量关系问题：建立“方程模型”解决
（5）测量问题：可设计成“图形模型”利用几何知识解决.
练习题
1．通过研究学生的学习行为，专家发现，学生的注意力随着老师讲课时间的变化而变化，讲课开始时，学生的兴趣激增；中间有一段时间，学生的兴趣保持较理想的状态，随后学生的注意力开始分散，设f(t)表示学生注意力随时间t（分钟）的变化规律（f(t)越大，表明学生注意力越集中），经过实验分析得知：
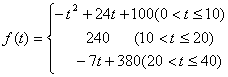
（1）讲课开始后多少分钟，学生的注意力最集中？能持续多少分钟？
（2）讲课开始后5分钟与讲课开始后25分钟比较，何时学生的注意力更集中？
（3）一道数学难题，需要讲解24分钟，并且要求学生的注意力至少达到180，那么经过适当安排，老师能否在学生达到所需的状态下讲授完这道题目？
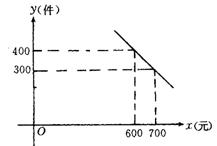2．某公司试销一种成本单价为500元／件的新产品，规定试销时的销售单价不低于成本单价，又不高于800元／件．经试销调查，发现销售量y（件）与销售单价x（元／件）之间近似于如图所示的一次函数y＝kx＋b的关系．
（1）根据图象，求一次函数y＝kx＋b的解析式；
（2）设公司获得毛利润（毛利润＝销售总价－成本总价）为S元．
① 试用销售单价x表示毛利润S．
② 试问销售单价定为多少时，此公司获得最大毛利润？最大毛利润是多少？此时的销售量是多少？
3．某公司生产的A种产品，它的成本是2元，售价是3元，年销售量为100万件。为了获得更好的效益，公司准备拿出一定的资金做广告。根据经验，每年投入的广告费是x（十万元）时，产品的年销售量将是原销售量的y倍，且y是x的二次函数，它们的关系如下表：
|
| 0 | 1 | 2 | … |
| y | 1 | 1.5 | 1.8 | … |
（1）求y与
之间的函数关系式；
（2）如果把利润看作是销售总额减去成本费和广告费，试写出年利润S（十万元）与广告费（十万元）的函数关系式；
（3）如果投入的年广告费为10 ~ 30万元，问广告费在什么范围内，公司获得的年利润随广告费的增大而增大？
4．为了在如图所示的直河道旁建造一个面积为5000m2的矩形堆物场，需砌三面砖墙BC、CD、DE，出于安全原因，沿着河道两边需向外各砌10m长的防护砖墙AB、EF，若当BC的长为xm时，所砌砖墙的总长度为ym，且在计算时，不计砖墙的厚度，求
（1）y关于x的函数解析式y=f(x);
（2）若BC的长不得超过40m，则当BC为何值时，y有最
小值，并求出这个最小值.
5． 已知某海滨浴场的海浪高度y（米）是时间t(0≤t≤24，单位小时）的函数，记作y=f(t)，下表是某日各时的浪高数据
| t（时） | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y（米） | 1.5 | 1.0 | 0.5 | 1.0 | 1.49 | 1 | 0.51 | 0.99 | 1.5 |
经长期观测y=f(t)的曲线可近似地看成函数y=Acosωt+b.
（1）根据以上数据，求出函数y=Acosωt+b的最小正周期T，振幅A及函数表达式；
（2）依据规定，当海浪高度高于1米时才对冲浪爱好者开放，请依据（1）的结论，判断一天内的上午8：00至晚上20：00之间，有多少时间可供冲浪者进行运动.
6．一个盒子中装有标号为1，2，3，4，5的5张标签，随机地选取两张标签，根据下列条件求两张标签上的数字为相邻整数的概率：
(1) 标签的选取是无放回的；
(2) 标签的选取是有放回的．
7．已知舰A在舰B的正东，距离6公里，舰C在舰B的北偏西30°，距离4公里，它们准备围找海洋动物，某时刻舰A发现动物信号，4秒后，舰B，C同时发现这种信号，A于是发射麻醉炮弹，设舰与动物都是静止的，动物信号的传播速度为1公里/1秒，求舰A炮击的方位角。
分析：求方位角应在水平面内求，所以应建立直角坐标系。
8．制定投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目. 根据预测，甲、乙项目可能的最大盈利率分别为100﹪和50﹪，可能的最大亏损率分别为30﹪和10﹪. 投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元. 问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？
9．甲、乙两艘轮船都要在某个泊位停靠6小时，假定它们在一昼夜的时段中随机地到达，试求这两艘轮船中至少有一艘在停靠泊位时必须等待的概率．
10．某县与沙漠化进行长期的斗争． 全县面积为 p， 2002 年底绿化率达 ，从 2003 年开始，每年绿化原有沙漠面积的 ，但与此同时，原有绿化面积的 被沙化． 设2002 年底的绿化面积为 a1，经过 n 年后的绿化面积为 an+1 ．
(I) 求2003年底的绿化面积
(II ) 经过多少年后，绿化率达?
11．某观测站C在城A的南20˚西的方向上，由A城出发有一条公路，走向是南40˚东，在C处测得距C为31千米的公路上B处有一人正沿公路向A城走去，走了20千米后，到达D处，此时C、D间距离为21千米，问这人还需走多少千米到达A城？
12．为促进个人住房商品化的进程，我国1999年元月公布了个人住房公积金贷款利率和商业性贷款利率如下：
| 贷款期(年数) | 公积金贷款月利率(‰) | 商业性贷款月利率(‰) |
| …… 11 12 13 14 15 …… | …… 4.365 4.455 4.545 4.635 4.725 …… | …… 5.025 5.025 5.025 5.025 5.025 …… |
汪先生家要购买一套商品房，计划贷款25万元，其中公积金贷款10万元，分十二年还清；商业贷款15万元，分十五年还清．每种贷款分别按月等额还款，问：
(1)汪先生家每月应还款多少元?
(2)在第十二年底汪先生家还清了公积金贷款，如果他想把余下的商业贷款也一次性还清；那么他家在这个月的还款总数是多少?
(参考数据：1.004455144＝1.8966，1.005025144＝2.0581，1.005025180＝2.4651)
参考答案
1．解：（1）当
，
是增函数，且
；
，
是减函数，且
.所以，讲课开始10分钟，学生的注意力最集中，能持续10分钟.
（2）
，故讲课开始25分钟时，学生的注意力比讲课开始后5分钟更集中.
当
时，
；当
，
（3）令
，则学生注意力在180以上所持续的时间28.57－4=24.57＞24，所以，经过适当安排，老师可以在学生达到所需要的状态下讲授完这道题.
2．分析：（1）本题把一次函数、二次函数及其有关计算问题赋予实际意义，把市场经济引进初中数学．观察图象可知，直线y＝kx＋b经过（600，400）、（700，300）两点，利用待定系数法即可求出其解析式；（2）根据公式“毛利润＝销售总价－成本总价”，得S＝xy－500y．
（2）本题的解答要实现由一次函数向二次函数的转化，即要灵活运用一次函数和二次函数的有关知识，并要考虑题设中对单价的限制，把求得的值代入检验，看是否符合要求．
解：（1）把（600，400），（700，300）两点的坐标分别代入y＝kx＋b，得
解得
∴ y＝－x＋1000，其中x的取值范围是500≤x≤800．
（2）① S＝xy－500y
＝x（－x＋1000）－500（－x＋1000），
即 S＝－x2＋1500x－500000（500≤x≤800）．
② S＝－x2＋1500x－500000＝－（x－750）2＋62500．
当x＝750时，S最大值＝62500．
此时y＝－x＋1000＝－750＋1000＝250（件）．
故当销售单价定为750件时，此公司获得最大毛利润62500元；此时的销售量是250件．
3．解：（1）设二次函数的解析式为y＝ax2＋bx＋c．
由关系表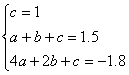，得
解得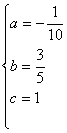
∴ 函数的解析式为y＝－
x2＋
x+1．
（2）根据题意，得
（3）
故当年广告费为10 ~ 25万元之间，公司获得的年利润随广告费的增大而增大
4．解：（1）
（2）令
得
因此
在（0，40]内递减，故y的最小值为f(40)=225m, x=40m.
5．解：（1）由表中数据，知T=12，ω=
.
由t=0,y=1.5得A+b=1.5.
由t=3,y=1.0,得b=1.0.所以，A=0.5,b=1.振幅A=
，
∴y=
(2)由题意知，当y>1时，才可对冲浪者开放.∴>1, 
>0.∴2kπ–
,即有12k–3<t<13k+3.
由0≤t≤24,故可令k=0,1,2,得0≤t<3或9<t<15或21<t≤24.
∴在规定时间内有6个小时可供冲浪者运动即上午9：00至下午15：00.
6．解：(1) 无放回地从5张标签随机地选取两张标签的基本事件有{1，2}，{1，3}，{1，4}，{1，5}，{2，3}，{2，4}，{2，5}，{3，4}，{3，5}，{4，5}总数为2×10个 ， 两张标签上的数字为相邻整数基本事件为{1，2}，{2，3}，{3，4}，{4，5}总数为2×4个。
∴P=
(2) 有放回地从5张标签随机地选取两张标签的基本事件有{1，2}，{1，3}，{1，4}，{1，5}，{2，3}，{2，4}，{2，5}，{3，4}，{3，5}，{4，5}和（1，1），（2，2），（3，3），（4，4），（5，5）总数为2×10+5=25个。
∴P=
7．分析：求方位角应在水平面内求，所以应建立直角坐标系。
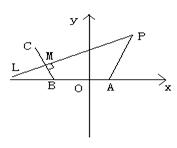解：为确定海洋动物的位置，首先的直线BA为x轴，线段BA的中垂线为y轴建立直角坐标系（如图），据题设，得B(-3,0), A(3,0), C(-5, 2
)且动物P(x,y)在BC的中垂线l上，
∵BC中点M的坐标为(-4,)， kBC=-.
∴ l的方程为y-=
(x+4)即：y=(x+7).................①
又∵ PB-PA=4(公里)
∴ P又在以B，A为焦点的双曲线右支上。
双曲线方程为
=1 (x≥2)...............②
由①②消去y得 11x2-56x-256=0，解的x1=-
(舍去)， x2=8。
∴ P点坐标为(8,5), 于是tg∠xAP=kAP=
=,
∴ ∠xAP=60°, 故舰A炮击的方位角为北偏东30°。
8．解：设投资人分别用x万元、y万元投资甲、乙两个项目.
由题意知
目标函数z=x+0.5y.
上述不等式组表示的平面区域如图所示，阴影部分（含边界）即可行域.
作直线
，并作平行于直线
的一组直线
与可行域相交，其中有一条直线经过可行域上的M点，且
与直线
的距离最大，这里M点是直线
和
的交点.
解方程组
得x=4，y=6
此时
（万元）.
当x=4，y=6时z取得最大值.
答：投资人用4万元投资甲项目、6万元投资乙项目，才能在确保亏损不超过1.8万元的前提下，使可能的盈利最大.
说明：本题主要考查简单线性规划的基本知识，以及运用数学知识解决实际问题的能力。
9．解：设甲到达时间为x，乙到达时间为y，则0<x , y<24．
若至少有一艘在停靠泊位时必须等待，
则0<y-x<6或0<x-y<6
必须等待的概率为：1-
=
10．解：(I ) 已知a1 = p，a2 = a1 (1－)+( p－a1)=a1 +p =p，
∴ 2003年底的绿化面积为p；
(II ) an+1 = an (1－)+( p－an)= an +p ， (n Î N*)
∴ (an+1－p)= (an－p) ∴(an+1－p)= (a1－p) ( )n
∴ an+1 = p－p () n
∴ p－p ( ) n >p Û >( ) n Û n≥5．
∴ 五年后绿化率达
11．解：根据题意得图02，其中BC=31千米，BD=20千米，CD=21千米，
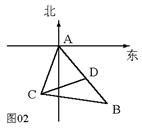∠CAB=60˚．设∠ACD = α ，∠CDB = β ．
在△CDB中，由余弦定理得：
，
．
．
在△ACD中，由正弦定理得：
．
此人还得走15千米到达A城．
说明：运用解三角形的知识解决实际问题时，关键是把题设条件转化为三角形中的已知元素，然后解三角形求之．
12． 解 设月利率为r，每月还款数为a元，总贷款数为A元，还款期限为n月
第1月末欠款数 A(1＋r)－a
第2月末欠款数 [A(1＋r)－a](1＋r)－a＝ A(1＋r)2－a (1＋r)－a
第3月末欠款数 [A(1＋r)2－a (1＋r)－a](1＋r)－a
＝A(1＋r)3－a (1＋r)2－a(1＋r)－a
……
第n月末欠款数 
得：
对于12年期的10万元贷款，n＝144，r＝4.455‰
∴
对于15年期的15万元贷款，n＝180，r＝5.025‰
∴
由此可知，汪先生家前12年每月还款942.37＋1268.22＝2210.59元，后3年每月还款1268.22元．