高三文科数学立体几何专题

2008届高三文科数学第二轮复习资料

——《立体几何》专题

一、空间基本元素：直线与平面之间位置关系的小结．如下图：

条件  结论	线线平行	线面平行	面面平行	垂直关系
线线平行	如果a∥b，b∥c，那么a∥c	如果a∥α，aβ，β∩α=b，那么a∥b	如果α∥β，α∩γ=a，β∩γ=b，那么a∥b	如果a⊥α，b⊥α，那么a∥b
线面平行	如果a∥b，aα，bα，那么a∥α	——	如果α∥β，aα，那么α∥β	——
面面平行	如果aα，bα，cβ，dβ，a∥c，b∥d，a∩b=P，那么α∥β	如果aα，bα,a∩b=P,a∥β,b∥β，那么α∥β	如果α∥β，β∥γ，那么α∥γ	如果a⊥α，a⊥β，那么α∥β

条件  结论	线线垂直	线面垂直	面面垂直	平行关系
线线垂直	二垂线定理及逆定理	如果a⊥α，bα，那么a⊥b	如果三个平面两两垂直，那么它们交线两两垂直	如果a∥b，a⊥c，那么b⊥c
线面垂直	如果a⊥b，a⊥c，bα，cα，b∩c=P，那么a⊥α	——	如果α⊥β，α∩β=b，aα,a⊥b，那么a⊥β	如果a⊥α，b∥a，那么b⊥α
面面垂直	定义（二面角等于900）	如果a⊥α，aβ，那么β⊥α	——	——

二、练习题：

1．l₁∥l₂，a，b与l₁，l₂都垂直，则a，b的关系是

 A．平行　　　B．相交　　  C．异面　　　D．平行、相交、异面都有可能

2．三棱柱ABC—A₁B₁C₁的体积为V，P、Q分别为AA₁、CC₁上的点，且满足AP=C₁Q，则四棱锥B—APQC的体积是

A．　　　　  B．　　　　 C．　　　　 D．

3．设、、为平面， 、、为直线，则的一个充分条件是

A．　　　　　  　B．

C．　　　　　　　  D．

4．如图1，在棱长为的正方体中， P、Q是对角

线上的点，若，则三棱锥的体积为

　 A．　 B．　 C．　　D．不确定

5．圆台的轴截面面积是Q，母线与下底面成60°角，则圆台的内切球的表面积是

　 A 　　 BQ　　　CQ　　　DQ　

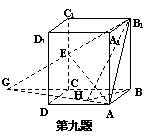
6．在正方体ABCD—A₁B₁C₁D₁中，E、F、G、H分别为棱BC、CC₁、C₁D₁、AA₁的中点，O为AC与BD的交点（如图），求证：

（1）EG∥平面BB₁D₁D；

（2）平面BDF∥平面B₁D₁H；

（3）A₁O⊥平面BDF；

（4）平面BDF⊥平面AA₁C．

7．如图，斜三棱柱ABC—A’B’C’中，底面是边长为a的正三角形，

侧棱长为 b，侧棱AA’与底面相邻两边AB、AC都成45⁰角，求

此三棱柱的侧面积和体积．

8．在三棱锥P—ABC中，PC=16cm，AB=18cm，PA=PB=AC=BC=17cm，求三棱锥的体积V_P-ABC．

9．如图6为某一几何体的展开图，其中是边长为6的正方形，SD=PD=6，CR=SC，AQ=AP，点S、D、A、Q及P、D、C、R共线.

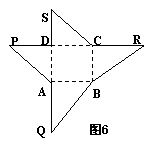　沿图中虚线将它们折叠起来，使P、Q、R、S四点重合，请画出其直观图，试问需要几个这样的几何体才能拼成一个棱长为6的正方体？

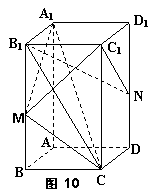
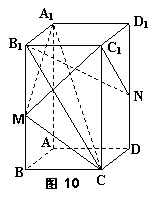10． 如图10，在正四棱柱ABCD-A₁B₁C₁D₁中，AB=，

AA₁=2，M、N分别是BB₁、DD₁的中点．

（1）求证：平面A₁MC₁⊥平面B₁NC₁；

（2）若在正四棱柱ABCD-A₁B₁C₁D₁的体积为V，

三棱锥M-A₁B₁C₁的体积为V₁，求V₁：V的值．

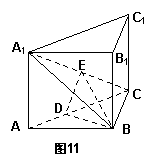11．直三棱柱ABC-A₁B₁C₁中，，E是A₁C的中点，

且交AC于D， (如图11) ．

 （I）证明：平面；

　 （II）证明：平面．

参考答案

1．D　　  2．B　　 3．D　　  4．A　　 5．D　

6．解析：（1）欲证EG∥平面BB₁D₁D，须在平面BB₁D₁D内找一条与EG平行的直线，构造辅助平面BEGO’及辅助直线BO’，显然BO’即是．

　 （2）按线线平行线面平行面面平行的思路，

在平面B₁D₁H内寻找B₁D₁和O’H两条关键的相交直线，

转化为证明：B₁D₁∥平面BDF，O’H∥平面BDF．

（3）为证A₁O⊥平面BDF，由三垂线定理，易得BD⊥A₁O，

再寻A₁O垂直于平面BDF内的另一条直线．

猜想A₁O⊥OF．借助于正方体棱长及有关线段的关系

计算得：A₁O²+OF²=A₁F²A₁O⊥OF．

　 （4）∵ CC₁⊥平面AC，∴ CC₁⊥BD

又BD⊥AC，∴ BD⊥平面AA₁C

又BD平面BDF，∴ 平面BDF⊥平面AA₁C

7．解析：在侧面AB’内作BD⊥AA’于D，连结CD．

∵ AC=AB，AD=AD，∠DAB=∠DAC=45⁰

∴ △DAB≌△DAC

∴ ∠CDA=∠BDA=90⁰，BD=CD

∴ BD⊥AA’，CD⊥AA’

∴ △DBC是斜三棱柱的直截面

在Rt△ADB中，BD=AB·sin45⁰=

∴ △DBC的周长=BD+CD+BC=(+1)a，△DBC的面积=

∴ S_侧=b(BD+DC+BC)=(+1)ab

∴ V=·AA’=

8．解析：取PC和AB的中点M和N

∴

在△AMB中，AM²=BM²=17²-8²=25×9

∴ AM=BM=15cm，MN²=15²-9²=24×6

∴ S_△AMB=×AB×MN=×18×12=108(cm²)

∴ V_P-ABC=×16×108=576(cm³)

9．解：它是有一条侧棱垂直于底面的四棱锥（如图）．

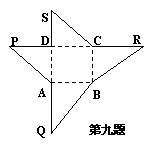　　　 需要3个这样的几何体可以拼成一个正方体.

10．解：（1）取CC₁的中点P，联结MP、NP、D₁P(图18)，

则A₁MPD₁为平行四边形　∴ D₁P∥A₁M，∵A₁B₁C₁D₁是边长

为的正方形，又C₁P=，

∴C₁PND₁也是正方形，∴C₁N⊥D₁P．∴C₁N⊥A₁M．

又 C₁B₁⊥A₁M，∴ A₁M⊥平面B₁NC₁，又A₁M平面A₁MC₁，

∴平面A₁MC₁⊥平面B₁NC₁；

（2）V= ，V_M-A1B1C1=V_C-MA1B1=，∴ V₁：V =　　

11．证明：（I）证： 三棱柱中，

又平面，且平面，

平面

（II）证：三棱柱中，

中，，是等腰三角形．

E是等腰底边的中点，

 

　　 又依条件知 　　　　　

且

　　由①，②，③得平面EDB．