09届高三数学摸底考试题
出题人:吴志刚 2008.8.5
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合![]() ,则满足条件
,则满足条件![]() 的集合P的个数是( )
的集合P的个数是( )
A.1个 B.2个 C.4个 D.8个
2.如果复数![]() (其中
(其中![]() 为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于
( )
为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于
( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
3.已知O为直角坐标系原点,P、Q的坐标满足不等式组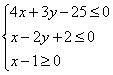 ,则
,则![]() 的最小值为( )
的最小值为( )
A、![]() B、
B、![]() C、
C、![]() D、0
D、0
4. 在锐角△ABC中,A>B,则下列四个不等式中
①sinA>sinB ②cosA<cosB ③sin2A>sin2B ④cos2A<cos2B
正确的有( )
A.①③ B.②③ C.①②③ D.①②④
5.已知函数![]() 在
在![]() 处的导数为1,则
处的导数为1,则![]() 等于( )
等于( )
A.![]() B.1
C.2
D.
B.1
C.2
D.![]()
6. 若两个函数的图象经过若干次平依后能够重合,则称这两个函数为“同形”函数,给出下列三个函数:![]()
![]() ,
,![]() 则( )
则( )
A ![]() 为“同形”函数
为“同形”函数
B ![]() 为“同形”函数,且它们与
为“同形”函数,且它们与![]() 不为“同形”函数
不为“同形”函数
C ![]() 为“同形”函数,且它们与
为“同形”函数,且它们与![]() 不为“同形”函数
不为“同形”函数
D ![]() 为“同形”函数,且它们与
为“同形”函数,且它们与![]() 不为“同形”函数
不为“同形”函数
7. 在棱长为1的正方体ABCD-A1B1C1D1中,M 为BB1的中点,则点D到直线A1M的距离为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8. 已知![]() ,则S的最小值是( )
,则S的最小值是( )
A.0
B.2
C.4
D.![]()
9. 现有五种不同的作物种选种在如图四块不同的试验田里,每块种植一种作物,且同一种作物不相邻,则不同的种植方法有 ( )
A.120 B.200 C.220 D.260
10.椭圆![]() 与直线
与直线![]() 交于A、B两点,过原点与线段AB中点的直线的斜率为
交于A、B两点,过原点与线段AB中点的直线的斜率为![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.一次研究性课堂上,老师给出函数![]() ,三位同学甲、乙、丙在研究此函数时分别给出命题:
,三位同学甲、乙、丙在研究此函数时分别给出命题:
甲:函数f (x)的值域为(-1,1);
乙:若x1≠x2,则一定有f (x1)≠f (x2);
丙:若规定![]() 对任意
对任意![]() 恒成立.
恒成立.
你认为上述三个命题中正确的个数有 ( )
A.0个 B.1个 C.2个 D.3个
12.已知![]() ,过
,过![]() 任作一条直线交抛物线
任作一条直线交抛物线![]() 于P、Q两点,若
于P、Q两点,若![]() 为定值,则
为定值,则![]() (
)
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中的横线上)
13.已知双曲线![]() 的右焦点为F,右准线与一条渐近线交于点A,
的右焦点为F,右准线与一条渐近线交于点A,
△OAF的面积为![]() (O为坐标原点),则双曲线的两条渐近线的夹角为
.
(O为坐标原点),则双曲线的两条渐近线的夹角为
.
14.若函数![]() 上增函数,则实数a的取值范围是 .
上增函数,则实数a的取值范围是 .
15.设A=![]() ,B=
,B=![]() ,记A☉B=max
,记A☉B=max![]() ,若A=
,若A=![]() ,B=
,B=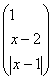 ,且A☉B=
,且A☉B=![]() ,则
,则![]() 的取值范围为
。
的取值范围为
。
16.直角坐标系中横坐标、纵坐标均为整数的点称为格点,如果函数f (x)的图象恰好通过k个格点,则称函数f (x)为k阶格点函数.下列函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 其中是一阶格点函数的有
.(填上所有满足题意的序号)
其中是一阶格点函数的有
.(填上所有满足题意的序号)
三、解答题:本大题共6小题,共74分. 解答应写出文字说明,证明过程或演算步骤.
17.(12分)已知向量![]() .
.
![]()
(1)当![]() ,求
,求![]() 的最大值
的最大值
(2)设函数![]() ,将函数
,将函数![]() 的图象按向量
的图象按向量![]() 平移后得到函数
平移后得到函数![]()
的图象,且![]() 求
求![]() 的最小值。
的最小值。
18.(12分)![]() 先生的鱼缸中有7条鱼,其中6条青鱼和1条黑鱼,计划从当天开始,每天中午从该鱼缸中抓出1条鱼(每条鱼被抓到的概率相同)并吃掉.若黑鱼未被抓出,则它每晚要吃掉1条青鱼(规定青鱼不吃鱼).(1)求这7条鱼中至少有5条被
先生的鱼缸中有7条鱼,其中6条青鱼和1条黑鱼,计划从当天开始,每天中午从该鱼缸中抓出1条鱼(每条鱼被抓到的概率相同)并吃掉.若黑鱼未被抓出,则它每晚要吃掉1条青鱼(规定青鱼不吃鱼).(1)求这7条鱼中至少有5条被![]() 先生吃掉的概率.(2)以
先生吃掉的概率.(2)以![]() 表示这7条鱼中被
表示这7条鱼中被![]() 先生吃掉的鱼的条数,求
先生吃掉的鱼的条数,求![]() .
.
19.(12分)如图,四棱锥P-ABCD的底面为正方形,PA⊥平面ABCD,AB=2,PC与平面ABCD成45°角,E、F分别为PA、PB的中点。
(1)求异面直线DE与AF所成角的大小;
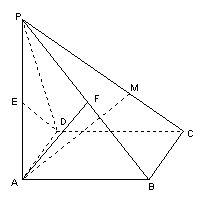 (2)设M是PC上的动点,试问当M在何处时,才能使AM⊥平面PBD,证明你的结论
(2)设M是PC上的动点,试问当M在何处时,才能使AM⊥平面PBD,证明你的结论
20.(12分)已知:在函数![]() 的图象上,以
的图象上,以![]() 为切点的切线的倾斜角为
为切点的切线的倾斜角为![]() .
.
(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)是否存在最小的正整数![]() ,使得不等式
,使得不等式![]() 对于
对于![]() 恒成立?如果存在,请求出最小的正整数
恒成立?如果存在,请求出最小的正整数![]() ;如果不存在,请说明理由;
;如果不存在,请说明理由;
22.已知数列![]() 的前n项和为
的前n项和为![]() ,满足
,满足![]() (n∈N
(n∈N![]() )
)
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)若数列![]() 满足
满足![]() ,
,![]() 为数列
为数列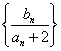 的前n项和,求证
的前n项和,求证![]() .
.
(3)数列![]() 中是否存在三项
中是否存在三项![]() 成等差数列?或存在,请求出一组适合条件的项;若不存在,请说明理由.
成等差数列?或存在,请求出一组适合条件的项;若不存在,请说明理由.
| |
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | A | B | D | A | B | C | B | B | A | D | D |
二、填空题:
13.
60° 14. ![]() 15. [1,1+
15. [1,1+![]() ] 16. ①②④
] 16. ①②④
三、解答题:
17. 解:(1)![]()
![]() …………3分
…………3分
![]() 的最大值为
的最大值为![]() ……6分
……6分
(2)![]() ………8分
………8分 ![]()
![]() …10分
…10分![]()
![]() 时得
时得![]() …………12分
…………12分
18. 解.(1)![]() 先生能吃到的鱼的条数
先生能吃到的鱼的条数![]() 可取4,5,6,7,最坏的情况是只能吃到4条鱼:前3天各吃掉1条青鱼,其余3条青鱼被黑鱼吃掉,第4天
可取4,5,6,7,最坏的情况是只能吃到4条鱼:前3天各吃掉1条青鱼,其余3条青鱼被黑鱼吃掉,第4天![]() 先生吃掉黑鱼,其概率为
先生吃掉黑鱼,其概率为
![]()
故![]() 先生至少吃掉5条鱼的概率是
先生至少吃掉5条鱼的概率是![]() .………6分
.………6分
(2)与(1)相仿地可得,
![]()
故![]() ,故所求期望值为5. ………12分
,故所求期望值为5. ………12分
19.  解:(1)如图,∵PA⊥平面ABCD
解:(1)如图,∵PA⊥平面ABCD
∴∠PCA为PC与平面ABCD所成角
∴∠PCA=45° ∴PA=AC=2
取DC的中点G,连EF、FG ∵E、F分别
为PA、PB的中点
∴四边形DEFG为平行四边形
∴DE∥FG ∴∠AFG为异面直线DE与AF
所成角或其补角, 连AG, 则FG=DE=,
AF=PB=, AG= ∴cos∠AFG== ∴∠AFG=arccos 即异面直线DE与AF所成角等于arccos…………6分
(2)过A作AH⊥PD于H,过H作HM交PC于M,则M点为所求
∵BD⊥平面PAC,∴BD⊥AM ∵CD⊥PD ∴PD⊥HM ∵PD⊥AH
∴PD⊥平面AHM ∴PD⊥AM ∴AM⊥平面PBD 又∵PH= = = ∴DH= ∴= =2 即PM=2MC时,AM⊥平面PBD…………12分
20.解:(Ⅰ)![]() ,依题意,得
,依题意,得![]()
![]() ,即
,即![]() ,
,![]() .
.
∵ ![]() , ∴
, ∴ ![]() . ………… 4分
. ………… 4分
(Ⅱ)令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .…………8分
.…………8分
又![]() ,
,![]() ,
,![]() ,
,![]() .
.
因此,当![]() 时,
时,![]() .
.
要使得不等式![]() 对于
对于![]() 恒成立,则
恒成立,则![]() .
.
所以,存在最小的正整数![]() ,使得不等式
,使得不等式![]() 对于
对于
![]() 恒成立. …………12分
恒成立. …………12分
22.解:(1)当n∈N![]() 时,
时,![]() , ①
, ①
则当![]() ,n∈N
,n∈N![]() 时,S
时,S![]() =2a
=2a![]() -2(n-1).② ,
-2(n-1).② ,
①-②,得a![]() =2a
=2a![]() -2a
-2a![]() -2
-2
即a![]() =2a
=2a![]() +2, ∴a
+2, ∴a![]() +2=2(a
+2=2(a![]() +2),∴
+2),∴![]() =2
=2
当n=1时,S![]() =2a
=2a![]() -2,则a
-2,则a![]() =2,
=2,
∴{ a![]() +2}是以a
+2}是以a![]() +2为首项,以2为公比的等比数列 ∴a
+2为首项,以2为公比的等比数列 ∴a![]() +2=4·2
+2=4·2![]() ,
,
∴![]()
![]() ……………………5分
……………………5分
(Ⅱ)b![]() =log
=log![]() ( a
( a![]() +2)= log
+2)= log![]() 2
2![]() =n+1,
=n+1,
![]() =
=![]() ,
,
则T![]() =
=![]() +
+![]() +…+
+…+![]() ,③
,③ ![]() T
T![]() =
=![]() +…+
+…+![]() +
+![]() ④
④
③-④,得 ![]() T
T![]() =
=![]() +
+![]() +
+![]() +…+
+…+![]() -
-![]()
=![]() +
+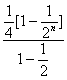
![]() =
= ![]() +
+![]() -
-![]() -
-![]() =
= ![]() -
-![]() ,
,
∴T![]() =
=![]() -
-![]() .
.
当n≥2时,T![]() -T
-T![]() =-
=-![]() >0,
>0,
∴{T![]() }为递增数列,∴T
}为递增数列,∴T![]() ≥T
≥T![]() =
=![]() ………………10分
………………10分
(3)若a![]() ,a
,a![]() ,a
,a![]() (r<s<t)构成等差数列且a
(r<s<t)构成等差数列且a![]() <a
<a![]() <a
<a![]() ,
,
则只能是a![]() +a
+a![]() =2a
=2a![]() ,∴(2
,∴(2![]()
![]()
∴1+2![]() *
*
∵r<s<t,r、s、t均为正整数,
∴(*)式左边为奇数,右边为偶数,不能成立,因此数列{a![]() }中不存在可以构成等差数列的三项……………………14分
}中不存在可以构成等差数列的三项……………………14分