09届高三数学暑期测试
姓名 班级 学号
一、选择题(![]() )
)
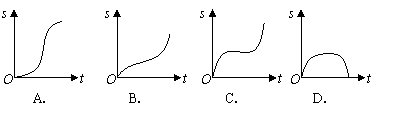
( )1.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程![]() 看作时间
看作时间![]() 的函数,其图像可能是
的函数,其图像可能是
( )2.设集合A={xx<-1或x>1},B={xlog2x>0},则A∩B=
A.{x x>1} B.{xx>0} C.{xx<-1} D.{xx<-1或x>1}
( )3![]() 已知等比数列
已知等比数列![]() 的首项为8,
的首项为8,![]() 是其前n项的和,某同学经计算得S2=20,S3=36,S4=65,后来该同学发现了其中一个数算错了,则该数为
是其前n项的和,某同学经计算得S2=20,S3=36,S4=65,后来该同学发现了其中一个数算错了,则该数为
A![]() S1 B
S1 B![]() S2
C
S2
C![]() S3 D
S3 D![]() S4
S4
( )4.函数![]() 的图象的一条对称轴方程是
的图象的一条对称轴方程是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
( )5.已知数列![]() 的通项公式是
的通项公式是![]() ,则该数列的最大项和最小项的和为
,则该数列的最大项和最小项的和为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
( )6.![]() 和
和![]() 是方程
是方程![]() 的两根,则
的两根,则![]() 与
与![]() 的关系是
的关系是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
( )7.等比数列![]()
A.1000 B.40 C.![]() D.
D.![]()
( )8.若![]() 则
则![]() =
=
(A)![]() (B)2
(C)
(B)2
(C)![]() (D)
(D)![]()
( )9.函数f(x)=2x-1,若a<b<c且f(a)>f(c)>f(b),则下列四个式子是成立的是
A.a<0,b<0,c<0 B.a<0,b≥0,c>0 C.2-a<2c D.2c+2a<2
( )10. 设数列![]() 的前n项和为Sn,令
的前n项和为Sn,令![]() ,称Tn为数列
,称Tn为数列![]() 的“理想数”,已知数列
的“理想数”,已知数列![]() 的“理想数”为2008,则数列2,
的“理想数”为2008,则数列2,![]() 的“理想数”为
的“理想数”为
A.2002 B.2004 C.2006 D.2008
二、填空题(![]() )
)
11.幂函数![]() 的图象经过点
的图象经过点![]() ,则
,则![]() 的解析式是 __.
的解析式是 __.
12.函数y=sinxcosx+sinx+cosx的最大值是 .
13.数列{an}满足递推式an=3an-1+3n-1(n≥2),又a1=5,则使得{![]() }为等差数列的实数λ=___ ___
}为等差数列的实数λ=___ ___
14.设函数f(x)=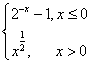 ,若f(x0)>1,则x0的取值范围是 。
,若f(x0)>1,则x0的取值范围是 。
15.将正整数排成下表: 1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
则数表中的2008出现在第![]() 行.
行.
16.一元二次方程![]() 的一根比1大,另一根比-1小,则实数a的取值范围是
的一根比1大,另一根比-1小,则实数a的取值范围是
17.已知t为常数,函数![]() 在区间[0,3]上的最大值为2,则t=___。
在区间[0,3]上的最大值为2,则t=___。
三、解答题(![]() )
)
18.(本小题满分14分)已知函数![]()
(Ⅰ)求函数![]() 的最小正周期和图象的对称轴方程
的最小正周期和图象的对称轴方程
(Ⅱ)求函数![]() 在区间
在区间![]() 上的值域
上的值域
19.(本小题满分14分)设数列![]()
(1)求证:![]() 是等差数列;
是等差数列;
(2)设![]() 对所有的
对所有的![]() 都成立的最大正整数m的值.
都成立的最大正整数m的值.
20.(本小题满分14分)函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() ,
,
(Ⅰ)求x<0时,![]() 的解析式;
的解析式;
(Ⅱ)问是否存在这样的正数a,b,当![]() 的值域为
的值域为![]() ?若存在,求出所有的a,b的值;若不存在说明理由.
?若存在,求出所有的a,b的值;若不存在说明理由.
21. (本小题满分15分)已知函数![]() 满足
满足![]() ,且对任意
,且对任意![]() 都有
都有![]() .
.
(1)求![]() 的值; (2)求
的值; (2)求![]() 的值;
的值;
(3)若![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围.
的取值范围.
22.(本小题满分15分)已知函数![]() 。
。
(Ⅰ)用a表示f(2)、f(3)并化简;
(Ⅱ)比较f(2)-2与f(1)-1,f(3)-3 与f(2)-2的大小关系,并由此归纳出一个更一般的结论(此结论不要求写出证明过程);
(Ⅲ)比较![]() 与
与![]() ,
,![]() 与
与![]() 的大小关系,并由此归纳出一个更一般的结论,并加以证明。
的大小关系,并由此归纳出一个更一般的结论,并加以证明。
答案
A 1.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程![]() 看作时间
看作时间![]() 的函数,其图像可能是
的函数,其图像可能是


A2.设集合A={xx<-1或x>1},B={xlog2x>0},则A∩B= ( )
A.{x x>1} B.{xx>0} C.{xx<-1} D.{xx<-1或x>1}
C3![]() 已知等比数列
已知等比数列![]() 的首项为8,
的首项为8,![]() 是其前n项的和,某同学经计算得S2=20,S3=36,S4=65,后来该同学发现了其中一个数算错了,则该数为
(
)
是其前n项的和,某同学经计算得S2=20,S3=36,S4=65,后来该同学发现了其中一个数算错了,则该数为
(
)
A![]() S1 B
S1 B![]() S2
C
S2
C![]() S3 D
S3 D![]() S4
S4
B4.函数![]() 的图象的一条对称轴方程是 ( )
的图象的一条对称轴方程是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
D5.已知数列![]() 的通项公式是
的通项公式是![]() ,则该数列的最大项和最小项的和为( )
,则该数列的最大项和最小项的和为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
A6.![]() 和
和![]() 是方程
是方程![]() 的两根,则
的两根,则![]() 与
与![]() 的关系是 ( )
的关系是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
D7.等比数列![]() ( )
( )
A.1000 B.40 C.![]() D.
D.![]()
B 8.若![]() 则
则![]() =
=
(A)![]() (B)2
(C)
(B)2
(C)![]() (D)
(D)![]()
D9.函数f(x)=2x-1,若a<b<c且f(a)>f(c)>f(b),则下列四个式子是成立的是( )
A.a<0,b<0,c<0 B.a<0,b≥0,c>0 C.2-a<2c D.2c+2a<2
C10. 设数列![]() 的前n项和为Sn,令
的前n项和为Sn,令![]() ,称Tn为数列
,称Tn为数列![]() 的“理想数”,已知数列
的“理想数”,已知数列![]() 的“理想数”为2008,则数列2,
的“理想数”为2008,则数列2,![]() 的“理想数”为( )
的“理想数”为( )
A.2002 B.2004 C.2006 D.2008
11.幂函数![]() 的图象经过点
的图象经过点![]() ,则
,则![]() 的解析式是 __.
的解析式是 __.![]() =
=![]()
12.函数y=sinxcosx+sinx+cosx的最大值是
.
![]()
13.数列{an}满足递推式an=3an-1+3n-1(n≥2),又a1=5,则使得{![]() }为等差数列的实数λ=___ - ___
}为等差数列的实数λ=___ - ___
14.设函数f(x)=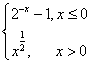 ,若f(x0)>1,则x0的取值范围是 。(-∞,-1)∪(1,+∞)
,若f(x0)>1,则x0的取值范围是 。(-∞,-1)∪(1,+∞)
15.将正整数排成下表: 1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
则数表中的2008出现在第![]() 行.45
行.45
16.一元二次方程![]() 的一根比1大,另一根比-1小,则实数a的取值范围是 -2<a<0
的一根比1大,另一根比-1小,则实数a的取值范围是 -2<a<0
17.已知t为常数,函数![]() 在区间[0,3]上的最大值为2,则t=___。1
在区间[0,3]上的最大值为2,则t=___。1
18.(本小题满分14分)
已知函数![]()
(Ⅰ)求函数![]() 的最小正周期和图象的对称轴方程
的最小正周期和图象的对称轴方程
(Ⅱ)求函数![]() 在区间
在区间![]() 上的值域
上的值域
18.解:(1)![]()
![]()
![]()
![]()
![]()
![]()
由![]()
![]() 函数图象的对称轴方程为
函数图象的对称轴方程为 ![]()
(2)![]()
因为![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,
上单调递减,
所以 当![]() 时,
时,![]() 取最大值 1
取最大值 1
又 ![]() ,当
,当![]() 时,
时,![]() 取最小值
取最小值![]()
所以 函数 ![]() 在区间
在区间![]() 上的值域为
上的值域为![]()
19.设数列![]() (1)求证:
(1)求证:![]() 是等差数列;
是等差数列;
(2)设![]() 对所有的
对所有的![]() 都成立的最大正整数m的值.
都成立的最大正整数m的值.
19.解:(1)依题意,![]() ,
,
当![]() ①
①
又![]() ②
②
②-①整理得:![]() 为等比数列,
为等比数列,
且![]()
![]() 是等差数列.
是等差数列.
(2)由(1)知,![]()
![]()
![]() 依题意有
依题意有![]()
故所求最大正整数m的值为5.
20.(本小题满分14分)函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() ,
,
(Ⅰ)求x<0时,![]() 的解析式;
的解析式;
(Ⅱ)问是否存在这样的正数a,b,当![]() 的值域为
的值域为![]() ?若存在,求出所有的a,b的值;若不存在说明理由.
?若存在,求出所有的a,b的值;若不存在说明理由.
20.(Ⅰ)当![]()
(Ⅱ)∵当![]()
若存在这样的正数a,b,则当![]()
∴f(x)在[a,b]内单调递减,∴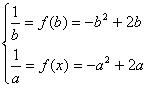
![]() 是方程
是方程![]() 的两正根,
的两正根,
![]()
21.已知函数![]() 满足
满足![]() ,且对任意
,且对任意![]() 都有
都有![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的值;
的值;
(3)若![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围.
的取值范围.
21.解:(1)由![]() ,令
,令![]() ,得
,得![]() ,∴
,∴![]() .
.
(2)由![]() ,
,![]() ,得
,得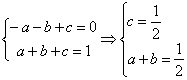 .
.
当![]() 时,
时,![]()
![]()
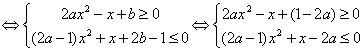
![]()
![]()
由①式![]() 显然不成立,∴
显然不成立,∴![]() ,∵
,∵![]() 的图象的对称轴为
的图象的对称轴为![]() ,∴Δ=
,∴Δ=![]() ,即
,即![]() ,∴
,∴![]() ,从而
,从而![]() ,而此时②式为
,而此时②式为![]() ,∴
,∴![]() .
.
(3)![]() ,设
,设![]() ,则
,则
![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() ,即
,即![]() 恒成立,而
恒成立,而![]() ,∴
,∴![]() ,
,
∴![]() .
.
22.(本小题满分15分,第一小问满分2分,第二小问满分4分,第三小问满分9分)
已知函数![]() 。
。
(Ⅰ)用a表示f(2)、f(3)并化简;
(Ⅱ)比较f(2)-2与f(1)-1,f(3)-3 与f(2)-2的大小关系,并由此归纳出一个更一般的结论(此结论不要求写出证明过程);
(Ⅲ)比较![]() 与
与![]() ,
,![]() 与
与![]() 的大小关系,并由此归纳出一个更一般的结论,并加以证明。
的大小关系,并由此归纳出一个更一般的结论,并加以证明。
(Ⅰ)![]()
![]() ………………………2分
………………………2分
(Ⅱ)![]()
![]() ,
,
一般地,f(n+1) -(n+1)> f(n) -n(n∈N*) …………………………………………6分
(Ⅲ) ![]() 所以
所以![]() ……………………………7分
……………………………7分
判断![]() ,证明如下:
,证明如下:
![]()
![]() (*)
(*)
因为![]() ,
,![]() ,所以(*)式显然成立,所以
,所以(*)式显然成立,所以![]() .…9分
.…9分
一般地![]() (n∈N*)
…………………………………………10分
(n∈N*)
…………………………………………10分
证明如下: ![]()
![]() >0
>0
![]() ,此式显然成立,故
,此式显然成立,故![]() (n∈N*)…………………15分
(n∈N*)…………………15分