高三(文科)数学第二次双周练试卷2008、8、7
制卷人:赵海晶 审核人:徐学兵
一、填空题(共70分)
1. ![]() 最小正周期为
最小正周期为![]() ,则
,则![]() ▲
▲
2. 若角![]() 的终边上有一点
的终边上有一点![]() ,则
,则![]() 的值是 ▲
的值是 ▲
3. 已知角![]() 的终边与函数
的终边与函数![]() 决定的函数图象重合,则
决定的函数图象重合,则![]() 的值为 ▲
的值为 ▲
4. 已知![]() ,则
,则![]() 值为
▲ .
值为
▲ .
5. 设扇形的半径长为![]() ,面积为
,面积为![]() ,则扇形的圆心角的弧度数是 ▲
,则扇形的圆心角的弧度数是 ▲
6. 函数![]() ▲
▲
7. 已知函数![]() ,则函数
,则函数![]() 的最小正周期是 ▲
的最小正周期是 ▲
8. 函数![]() 的单调递增区间是 ▲
的单调递增区间是 ▲
9. 方程![]() (
(![]() 为常数,
为常数,![]() )的所有根的和为 ▲
)的所有根的和为 ▲
10. 在△ABC中,已知![]() ,则△ABC为 ▲ 三角形
,则△ABC为 ▲ 三角形
11. 已知![]() ,则
,则![]() = ▲
= ▲
12. 当![]() 时,关于
时,关于![]() 的方程
的方程![]() 时有解,则
时有解,则![]() 的取值范围是 ▲
的取值范围是 ▲
13.函数![]() 所对应的曲线为“凸曲线”,此类函数具有的性质为
所对应的曲线为“凸曲线”,此类函数具有的性质为![]() ,类比此性质,设A,B,C为三角形的三个内角,则
,类比此性质,设A,B,C为三角形的三个内角,则![]() ▲
▲
14. 已知![]() ,且
,且![]() 在区间
在区间![]() 有最小值,无最大值,则
有最小值,无最大值,则![]() ▲
▲
二、解答题(共90分)
15. (14分) 在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的值; (2)求
的值; (2)求![]() 的值.
的值.
16. (14分)已知![]() ,函数
,函数![]() .
.
(1)求函数![]() 的单调增区间;;
的单调增区间;;
(2)若![]() , 求
, 求![]() 的值.
的值.
17.(15分)已知定义在R上的函数![]() 的周期为
的周期为![]() ,
,![]() ,且
,且![]() 的最大值为3。
的最大值为3。
(1)写出![]() 的表达式;
的表达式;
(2)写出函数![]() 的对称中心、对称轴方程;
的对称中心、对称轴方程;
(3) 说明![]() 的图象如何由函数
的图象如何由函数![]() 的图象经过怎样的变换得到。
的图象经过怎样的变换得到。
18. (15分)在![]() 中,
中,![]() 的对边分别为
的对边分别为![]() 且
且![]() 成 等差数列.
成 等差数列.
(1)求B的值;
(2)求![]() 的范围。
的范围。
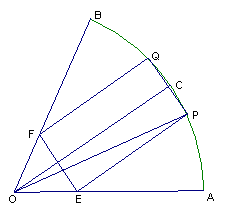 19. (16分)如图,在半径为R、圆心角为
19. (16分)如图,在半径为R、圆心角为![]() 的扇形金属材料中剪出一个长方形
的扇形金属材料中剪出一个长方形
EPQF,并且EP与![]() 的平分线OC平行,设
的平分线OC平行,设![]() 。
。
(1)试写出用![]() 表示长方形EPQF的面积
表示长方形EPQF的面积![]() 的函数,并求
的函数,并求![]() 的最大值
的最大值
(2)现用EP和FQ作为母线并焊接起来,将长方形EFPQ
制成圆柱的侧面,能否从![]() 中直接剪出一个圆面作为圆柱形容器的底面?如果不能请说明理由。
中直接剪出一个圆面作为圆柱形容器的底面?如果不能请说明理由。
20.(16分)设![]() ,函数
,函数![]() 的定义域为
的定义域为![]() ,且
,且![]()
![]() , 对定义域内任意的
, 对定义域内任意的![]() ,满足
,满足![]() ,
,
求:(1)![]() 及
及![]() 的值;
的值;
(2)函数![]() 的单调递增区间;
的单调递增区间;
(3)![]() 时,
时,![]() ,求
,求![]() ,并猜测
,并猜测![]()
![]() 时,
时,![]() 的表达式.
的表达式.
高三数学(文科)第二次双周练数学试卷(答案)
一、 填空题
1. ![]() 2.
2. ![]() 3.
3. ![]() 4. 7 5.
4. 7 5. ![]() 6. -5 7.
6. -5 7. ![]()
8.![]() 9.0 10. 等边 11.
9.0 10. 等边 11. ![]() 12.
12. ![]() 13.
13. ![]() 14.
14. ![]()
二、解答题
15. 解:(1)在![]() 中,
中,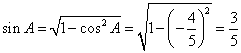 ,
,
由正弦定理,![]() .所以
.所以![]() .
.
(2)因为![]() ,所以角
,所以角![]() 为钝角,从而角
为钝角,从而角![]() 为锐角,于是
为锐角,于是
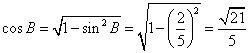 ,
,![]() ,
,
![]() .
.
![]()
![]()
![]()
16. 解(Ⅰ): ![]()
![]() .
.
由![]()
得 ![]()
![]()
![]()
![]() 增函数
增函数
(Ⅱ)由(Ⅰ)知![]() ,即
,即![]() ,
,
∴![]()
![]()
17. (1)![]() (2)对称中心为
(2)对称中心为![]() ;对称轴方程为
;对称轴方程为![]() (3)
(3)![]() 的图象可先由函数
的图象可先由函数![]() 的图象向左平移
的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,再将
的图象,再将![]() 图象的横坐标缩小到原来的
图象的横坐标缩小到原来的![]() ,得到
,得到![]() 的图象,再将
的图象,再将![]() 图象向上平移一个单位,即得
图象向上平移一个单位,即得![]() 的图象
的图象
18. 解:由![]() 成等差数列,
成等差数列,
![]()
![]()
由正弦定理得,![]()
代入得,![]()
即:![]()
![]()
![]()
又在![]() 中,
中,![]() ,
,![]()
![]()
因为![]() ,
,![]()
![]() .
.
(II)由![]() ,
,![]()
![]()
![]()
![]()
![]()
因为 ![]() ,
,![]()
![]()
![]() 的范围是
的范围是![]()
19. (1)![]()
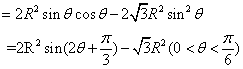
当![]() 时,即
时,即![]() ,
,![]() 取得最大值
取得最大值![]()
(2)依题意制成的圆柱的底面周长![]() =EF=
=EF=![]() ,则其半径为
,则其半径为![]()
在![]() 中,
中,![]()
故内切圆半径r=![]()
而![]() ,
,
所以能从![]() 中直接剪出一个圆面作为圆柱形容器的底面。
中直接剪出一个圆面作为圆柱形容器的底面。
20. 解(1)![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(2)![]() ,
,
![]() 的增区间为
的增区间为![]() .
.
(3)![]()
![]() ,
,![]() ,
,
所以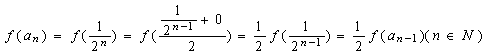 ,
,
因此![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,故
的等比数列,故![]() ,
,
猜测![]() .
.