高三数学第四轮模拟考试试卷
时间:120分钟 分值:160分 命题人:宋友强
一、 填空(每小题5分,共70分)
1. 设A,B是非空集合,定义![]() 。已知A = {x y = },B = { y y = 2 x,x > 0},则
。已知A = {x y = },B = { y y = 2 x,x > 0},则![]() ______
___。(教材改编)
______
___。(教材改编)
2. 若![]() 是纯虚数,则
是纯虚数,则![]() 的值为
.
的值为
.
3. 已知函数![]() 是定义在R上的偶函数,其减区间为
是定义在R上的偶函数,其减区间为![]() ,则不等式
,则不等式![]() 的解集是__________
______。(教材改编)
的解集是__________
______。(教材改编)
4. 在![]() 和
和![]() 之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为
。(苏教版必修5教材P49例2改编)
之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为
。(苏教版必修5教材P49例2改编)
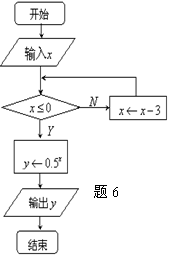 5. 一个空间几何体的主视图、左视图、俯视图为直角三角形,边长如图所示,那么这个几何体的体积为 .
5. 一个空间几何体的主视图、左视图、俯视图为直角三角形,边长如图所示,那么这个几何体的体积为 .
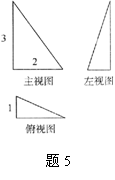 |
6. 下面是一个算法的程序框图,当输入的值![]() 为5时,则其输出的结果是 .
为5时,则其输出的结果是 .
7.曲线![]() 在
在![]() 处的切线方程为____________________。(改编题)
处的切线方程为____________________。(改编题)
8. 下面是按照一定规律画出的一列“树型”图:经观察可以发现:
图(2)比图(1)多出2个“树枝”;图(3)比图(2)多出5个“树枝”;
图(4)比图(3)多出10个“树枝”;

照此规律,图(7)比图(6)多出_______个“树枝”.
9.已知正四棱锥P—ABCD的高为4,侧棱长与底面所成的角为![]() ,则该正四棱锥的侧面积是__________。(苏教版必修2教材P51例1改编)
,则该正四棱锥的侧面积是__________。(苏教版必修2教材P51例1改编)
10. 圆心为![]() 且与直线
且与直线![]() 相切的圆的方程是___________.
相切的圆的方程是___________.
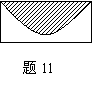
11. 下图的矩形,长为5,宽为2,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,则我们可以估计出阴影部分的面积为 .
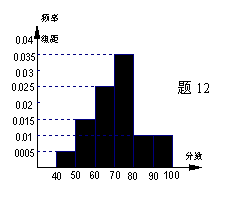 12. 统计某校1000名学生的数学会考成绩,得到样本频率分布直方图如右图示,规定不低于60分为及格,不低于80分为优秀,则及格人数是 ;优秀率为
。
12. 统计某校1000名学生的数学会考成绩,得到样本频率分布直方图如右图示,规定不低于60分为及格,不低于80分为优秀,则及格人数是 ;优秀率为
。
 |
13. 若函数![]() 在区间
在区间![]() 上单调递减,则实数m的范围是________.
上单调递减,则实数m的范围是________.
14. 给出下列四个命题:
①命题“![]() ”的否定是“
”的否定是“![]() ”;
”;
②线性相关系数r的绝对值越接近于1,表明两个随机变量线性相关性越强;
③若![]() ,则不等式
,则不等式![]() 成立的概率是
成立的概率是![]() ;
;
④函数![]() 上恒为正,则实数a的取值范围是
上恒为正,则实数a的取值范围是![]() 。
。
其中真命题的序号是 。(填上所有真命题的序号)
二、解答题(第15、16题,每题14分,第17、18题,每题15分,第19、20题,每题16分,)
15. 如图,在四棱锥P-ABCD中,底面为矩形ABCD,E,F分别为AB、PC中点,且PD=PE,
PB=PC.
 求证:(1)EF//平面PAD;(2)平面PDE⊥平面ABCD.
求证:(1)EF//平面PAD;(2)平面PDE⊥平面ABCD.
16. 在锐角三角形ABC中,已知内角A、B、C所对的边分别为a、b、c,且![]() .
.
(1)若![]() ,求A、B、C的大小;
,求A、B、C的大小;
(2)已知向量![]() 的取值范围.
的取值范围.
17. 某公司为帮助尚有26.8万元无息贷款没有偿还的残疾人商店,借出20万元将该商店改建成经营状况良好的某奥运品牌消费品专卖店,并约定用该店经营的利润逐步偿还债务(所有债务均不计利息).已知该种消费品的进价为每件40元;该店每月销售量q (x)(百件)与销售价x(![]() )(元/件)之间的关系是:(1)当
)(元/件)之间的关系是:(1)当![]() 时,月售量
时,月售量![]() (万件)是销售价格
(万件)是销售价格![]() (元)的二次函数,它们的关系如下表;(2)当
(元)的二次函数,它们的关系如下表;(2)当![]() 时,
时,![]() .职工每人每月工资为600元,该店应交付的其它费用为每月10000元.
.职工每人每月工资为600元,该店应交付的其它费用为每月10000元.
(Ⅰ)若当销售价x为50元/件时,该店正好收支平衡,求该店的职工人数;
(Ⅱ)若该店只安排40名职工,则该店最早可在几年后还清所有债务,此时每件消费品的价格定为多少元?(精确到年.已知![]() ,
,![]() )
)
| x | 40 | 50 | 60 |
| q(x) | 60 | 40 | 20 |
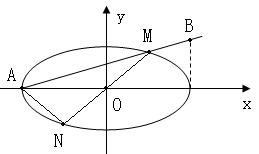
18.已知椭圆![]() 直线
直线![]() 过点A
过点A![]() 和点B
和点B![]() ,交椭圆于点M,直线MO交椭圆于N。
,交椭圆于点M,直线MO交椭圆于N。
(1)
用![]() 表示
表示![]() 的面积S;(2)若
的面积S;(2)若![]() ,求S的最大值。
,求S的最大值。
19. 对于函数![]() ,若存在
,若存在![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点。如果函数
的不动点。如果函数![]() 有且仅有两个不动点
有且仅有两个不动点![]() 、
、![]() ,且
,且![]() 。
。
(1)试求函数![]() 的单调区间;
的单调区间;
(2)已知各项不为零的数列![]() 满足
满足![]() ,求证:
,求证:![]() ;
;
(3)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证:![]() 。
。
20.已知![]() .
.
⑴ 求函数![]() 在
在![]() 上的最小值;
上的最小值;
⑵ 对一切![]() ,
,![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
⑶ 证明对一切![]() ,都有
,都有![]() 成立.
成立.
高三数学答案卷
 一、填空(每小题5分,共70分)
一、填空(每小题5分,共70分)
1. ;2. ;3. ;4. ;
5. ;6. ;7. ;8. ;
9. ;10. ;11. ;12. ;
13. ;14. .
二、解答题:

|
高三数学答案
一、填空:1. ![]() ;2.
;2. ![]() ;3.
;3. ![]() ;4. 216; 5. 1;6. 2;
;4. 216; 5. 1;6. 2;
7. ![]() ;8. 80;9.
;8. 80;9. ![]() ;10.
;10. ![]() ;11.
;11. ![]() ;
;
12. 800 20%;13. ![]() ;14. ②④。
;14. ②④。
15.
16. 解:由已知

![]()
(1)由已知
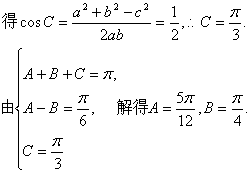
![]()
(2)3m-2n2=9 m 2+4n2-12 m·n =13-12(sinAcos B +cosAsin B)
=13-12sin(A+B)=13-12sin(2 B +![]() ).
).
∵△ABC为锐角三角形,A-B=![]() ,∴C=π-A-B<
,∴C=π-A-B<![]() ,A=
,A=![]() +B<
+B<![]() .
.
![]()
![]()
∴3m-2n2=∈(1,7).∴3m-2n的取值范围是(1,![]() )
)
17. (Ⅰ)设该店的月利润为S(x)元,有职工m名.则
![]() .
.
当![]() 时,设q (x)=
时,设q (x)=![]() ,由表得
,由表得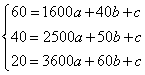 ,
,
解得q (x)=![]() .又由题设可知:
.又由题设可知:![]() .
.
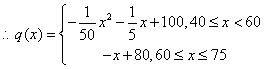
所以,
由已知,当![]() 时,
时,![]() ,即
,即
![]() ,
,
解得![]() .即此时该店有50名职工.
.即此时该店有50名职工.
(Ⅱ)若该店只安排40名职工,则月利润
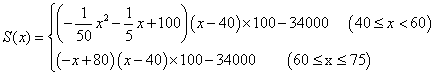 .
.
当![]() 时,
时,![]()
![]() ,令
,令![]() ,解得
,解得![]() (负值舍去),
(负值舍去),![]()
当![]() 时,
时,![]() ,当
,当![]() 时
时![]() ,
,
所以![]() 时,
时,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() 单调递减.
单调递减.
因为![]() 9186(元),
9186(元),![]() 9232(元)
9232(元)
所以,当![]() 时,
时,![]() 9232即为最大值.
9232即为最大值.
当![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() 取最大值6000元.
取最大值6000元.
综上,当![]() 时,S有最大值9232元.
时,S有最大值9232元.
设该店最早可在n年后还清债务,依题意,有
![]() .
.
解得![]() .
.
所以,该店最早可在5年后还清债务,此时消费品的单价定为55元.
18.
19. (1)设![]()
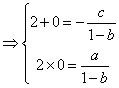 ∴
∴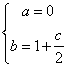 ∴
∴
由![]()
又∵![]() ∴
∴![]()
∴![]() …… 3分
…… 3分
于是![]()
由![]() 得
得![]() 或
或![]() ; 由
; 由![]() 得
得![]() 或
或![]()
故函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,
,
单调减区间为![]() 和
和![]() ……4分
……4分
(2)由已知可得![]() , 当
, 当![]() 时,
时,![]()
两式相减得![]()
∴![]() 或
或![]()
当![]() 时,
时,![]() ,若
,若![]() ,则
,则![]() 这与
这与![]() 矛盾
矛盾
∴![]() ∴
∴![]() ……6分
……6分
于是,待证不等式即为![]() 。
。
为此,我们考虑证明不等式![]()
令![]() 则
则![]() ,
,![]()
再令![]() ,
,![]() 由
由![]() 知
知![]()
∴当![]() 时,
时,![]() 单调递增 ∴
单调递增 ∴![]() 于是
于是![]()
即![]() ①
①
令![]() ,
,![]() 由
由![]() 知
知![]()
∴当![]() 时,
时,![]() 单调递增 ∴
单调递增 ∴![]() 于是
于是![]()
即![]() ②
②
由①、②可知![]() ……10分
……10分
所以,![]() ,即
,即![]() ……11分
……11分
(3)由(2)可知![]() 则
则![]()
在![]() 中令
中令![]() ,并将各式相加得
,并将各式相加得
![]()
即![]() ……14分
……14分
20. 解答:⑴ ![]() ,当
,当![]() ,
,![]() ,
,![]() 单调递减,当
单调递减,当![]() ,
,![]() ,
,![]() 单调递增.
单调递增.
① ![]() ,t无解;
,t无解;
② ![]() ,即
,即![]() 时,
时,![]() ;
;
③ ![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() ;
;
所以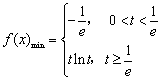 .
.
⑵ ![]() ,则
,则![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() 单调递增,
单调递增,![]() ,
,![]() ,
,![]() 单调递减,所以
单调递减,所以![]() ,因为对一切
,因为对一切![]() ,
,![]() 恒成立,所以
恒成立,所以![]() ;
;
⑶ 问题等价于证明![]() ,由⑴可知
,由⑴可知![]() 的最小值是
的最小值是![]() ,当且仅当
,当且仅当![]() 时取到,设
时取到,设![]() ,则
,则![]() ,易得
,易得![]() ,当且仅当
,当且仅当![]() 时取到,从而对一切
时取到,从而对一切![]() ,都有
,都有![]() 成立.
成立.