高三数学练习试题卷
一、填空题（本大题满分48分）本大题共有12小题，每题 4分。
1．函数y=
在区间 [2,5]上的值域是__________
2。等比数列{an}的首项为a1=a，公比q≠1，则
=_____
3
如果奇函数y=f(x) (x
0)，当x
(0,+
)时，f(x)=x-1，则使f(x-1)<0的x的取值范围是________________
4．抛物线y=
x2+2x的准线方程为__________________
5．
=___________
6．现有甲乙两船，其中甲船在某岛B的正南方A处，A与B相距7公里，甲船自A处以4公里/小时的速度向北方向航行，同时乙船以6公里/小时的速度自B岛出发，向北60o西方向航行，问_____分钟后两船相距最近？
7．有六根细木棒，其中较长的两条木棒长分别为
a、
a，其余四根木棒长均为a，请你用它们搭成一个三棱锥，其中较长的两条棱所在直线所成角的余弦值为_________
8若首项为a1,公比为q(q¹1)的等比数列{an}满足
(
-qn)=
,则a1的取值范围是__________.
9．某甲A篮球队的12名队员(含2名外援)中有5名主力队员(含一名外援)，主教练要从12名队员中选5人首发上场，则主力队员不少于4人，且有一名外援上场的概率是___________.
10．设复数z=x+yi(x,yR)且z-4i=z+2，则2x+4y的最小值为___________
11．右图是正方体的展开图，其中直线AB与CD
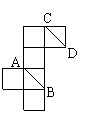在原正方体中所成角的大小是___________
12．集合S={1,2,3,4,5,6}，A是S的一个子集，
当xA时，若x-1
A，x+1A，则称x为A的一
个“孤立元素”，那么S中无“孤立元素”的4元子
集的个数是______________
二、选择题（本题满分16分）本大题4 小题，每题4分
13．已知向量
={cosa,sina}，
={cosb,sinb}，那么----------( )
A. 
B.
C.
D.
与的夹角为a+b
14．设函数f(x)=Asin(wx+
)(A>0,w>0,
)的图象关于直线x=
对称，它的周期是p，则以下命题错误的是------( )
A.
f(x)的图象过点
B.
f(x)在
上是减函数
C.
f(x)的一个对称中心是点
D.
f(x)的最大值为A
15．设x,yR+，且xy-(x+y)=1，则------------------------------------------------------( )
A.
x+y
+2 B.
xy
+1
C.
x+y
D.
xy
16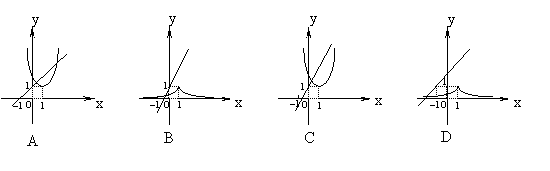
．已知函数
，在同一坐标系中，y=f -1(x)与y=
的图象可能是-----------------------------------------------------( )
三、解答题(本大题满分86分)本大题共有6题
17．（本题满分14分，第（1）小题6分，第（2）小题6分）
在△ABC中，角A、B、C的对应边分别为a、b、c，若lga-lgb=lgcosB-lgcosA
(1)判断△ABC的形状；
(2)若a、b满足：函数y=ax+3的图象与函数y=
x-b的图象关于直线y=x对称，求边长c.
18．（本题满分12分,第（1）小题5分，第（2）小题3
|
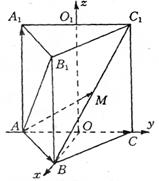
已知正三棱柱ABC—A1B1C1，底面边长AB=2，
AB1⊥BC1，点O、O1分别是边AC，A1C1的中点，建
立如图所示的空间直角坐标系.
（Ⅰ）求正三棱柱的侧棱长.
（Ⅱ）若M为BC1的中点，试用基向量
、
、
表示向量
；
（Ⅲ）求异面直线AM与BC所成角.
19．（本题满分12分第（1），小题4分，第（2）小题10分）
双曲线3x2-y2=1与直线ax-y+1=0相交于A、B两点.
(1)求a的取值范围；(2)a为何值时，ÐAOB>900 (其中O为原点)；
20．（本题满分16分第（1），小题8分，第（2）小题8分。）
设M(k)是满足不等式
的正整数x的个数，记S=M(1)+M(2)+…+M(n) n
.
(1)求S；(2)设t=5n-2+5n+2+n-2
(n),试比较S与t的大小.
21 （本小题满分16分）
程先生买了一套总价为80万元住房，首付30万元，其余50万元向银行申请贷款，贷款月利率0.5%,从贷款后的第一个月后开始还款，每月还款数额相等，30年还清。问程先生每月应还款多少元（精确到0.01元）
（注：如果上个月欠银行贷款a元，则一个月后，程先生应还给银行固定数额x元，此时贷款余额为a(1+0.5%)-x元）
22．（本题满分18分，第（1）小题6分，第（2）小题6分,第（3）小题6分）
如果实系数a1、b1、c1和a2、b2、c2都是非零常数.
(1)设不等式a1x2+b1x+c1>0和a2x2+b2x+c2>0的解集分别是A、B，试问
是A=B的什么条件？并说明理由。
（2）在实数集中，方程a1x2+b1x+c1=0和a2x2+b2x+c2=0的解集分别为A和B，试问 是A=B的什么条件？并说明理由。
(3)在复数集中，方程a1x2+b1x+c1=0和a2x2+b2x+c2=0的解集分别为A和B，
证明：是A=B的充要条件；
参考答案
一 填空题（每题4分，共48分）
1. [, 3]
2. 
3 ( - ∞,0)∪(1,2)
4 y= - 5 5. 1330 6 30
7. 
8. (0, )∪(,3)
9 
10 
11 600
12 6
二 选择题（每题4分，共16分）
13 C 14 A 15 A 16 C
三 解答题（本题共86分）
17 （1） 由lg
得 
, 于是
sin2A=sin2B ………………………………………… 4分
所以三角形ABC为等腰三角形或直角三角形。 ……………… 6分
（2） 因为y=ax+3的反函数
与函数
重合，所以a=3, b=1
…………………………………………… 10分
从而 
…………………………………………
12分
18 （1）设侧棱长为b,则A(0,-1,0), B1(
,0,b), B(,0,0), C1(0,1,b)
={,1,b},
={-,1,b}
…………………………3
分
∵ AB1 ⊥AB1
∴ -3+1+b2=0, b= 
…………5分
（2） 
…………………… 8分
（3） 设异面直线AM与BC所成角为α，
， 
………… 10分
， ∴ α=900 …………… 12分
19 （1）把直线方程y=ax+1代入双曲线方程得
(3-a2)x2-2ax-2=0
∆=24-4a2>0
∴ a∈(
…………… 4分
（2）因为∠AOB>900，所以原点在以AB为直径的圆外，AB中点(
圆方程为
………………7分
∴ 
(1+a2)
即 4(a2+9)>(24-4a2)(1+a2) ………………10分
得 1<a2<3
所以
…………12分
20 (1) 化简得 x2-26•25k-1x+252k-1≤0
∴ 25k-1≤x≤25k ………………3分
∴ M(k)=25k-25k-1+1 ………………5分
S=(251-250+1)+(252-251+1)+ …+(25n-25n-1+1)=25n+n-1………………8分
(2) 要 S-t= (52n-
…………11分
只要
5n>25
或 5n<
即 n>2 或 n<-2 ……………13分
∴ 当n>2 时s>t ; 当n=2时s=t; 当n=1时s<t …………16分
21 设程先生在第n 个月时还欠银行贷款an万元,每月固定还款x万元，则
an=an-1(1+0.5%)-x，a0=50 ……………5分
an+k=1.005(an-1+k)
an=1.005an-1+0.005k
所以 k=-200x, { an-200x }是公比为1.005的等比数列 ……………8分
即 an-200x=(a0-200x)•1.005n.
由a360=0得 0-200x=(50-200x) •1.005360. ……………13分
利用计算器可以求得 x=0.299775万元，即每月还款2997.75元………16分
22 （1） 是A=B的既不充分也不必要条件。 ………2分
若 a=b=c=1, a1=b1=c1= -1,则A≠B ………4分
若 A=B=Φ,则两个不等式的系数之间没有关系。 ………6分
（2）是A=B的充分也不必要条件
………8分
若 A=B=Φ,则两个方程的系数之间没有关系。 ………10分
由于两个方程的系数对应成比例，所以两个方程式同解方程。………12分
（3）是A=B的充要条件
………14分
由于两个方程的系数对应成比例，所以两个方程是同解方程。充分性得证。………16分
由韦达定理可以证明必要性。………18分