高三数学考前训练30题
1. 若曲线![]() 在点P处的切线平行于直线3x-y=0,则点P的坐标为
.
在点P处的切线平行于直线3x-y=0,则点P的坐标为
.
【解析】设![]() ,由
,由![]() ,得
,得![]() ,从而
,从而![]() .
.
![]() 点P的坐标为(1,0).
点P的坐标为(1,0).
2. 在△ABC中,角A、B、C的对边分别为![]() 、
、![]() 、
、![]() ,且
,且![]() ,则角B的大小是
.
,则角B的大小是
.
【解析】由余弦定理,得 ![]() .则
.则
![]() ,即
,即![]() .
.
所以B的大小是![]() 或
或![]() .
.
3.已知单位正方体ABCD-A1B1C1D1对棱BB1,DD1上有两个动点E、F,BE=D1F,设EF与面AB1所成角为α,与面BC1所成角为β,则α+β的最大值为 .
【解析】由对称性可知α=β,又![]() ,所以α≤45°,α+β≤90°.
,所以α≤45°,α+β≤90°.
4. 设函数![]() ,集合M=
,集合M=![]() ,P=
,P=![]() ,若M
,若M![]() P,则实数a的取值范围是
.
P,则实数a的取值范围是
.
【解析】设函数![]() , 集合
, 集合![]() .
.
若a>1时,M={x 1<x<a};
若a<1时,M={x a<x<1};
a=1时,M=![]() .
.
![]() ,∴
,∴![]() =
=![]() >0.
>0.
∴ a>1时,P=R,a<1时,P=![]() ;已知
;已知![]() ,所以 (1,+∞).
,所以 (1,+∞).
5. 已知命题P:.![]() ,
,![]() 不等式
不等式 ![]() 的解集为
的解集为![]() .如果
.如果![]() 和
和![]() 有且仅有一个正确,则
有且仅有一个正确,则![]() 的取值范围是
.
的取值范围是
.
【解析】若![]() 和
和![]() 都正确,则由
都正确,则由![]() ,有
,有![]() .由
.由![]() ,有
,有![]() 的解集为
的解集为![]() .
.
用函数认识不等式,只需![]() 的最小值
的最小值![]() 2
2![]() 此时
此时![]() .
.
若![]() 和
和![]() 都不正确,则由
都不正确,则由![]() ,有
,有![]() .由
.由![]() ,有
,有![]() 其交集为空集,此时
其交集为空集,此时![]() 不存在.
不存在.
由题设知,![]() ,用补集思想,所求
,用补集思想,所求![]() 的取值范围为
的取值范围为![]() .
.
6. 己知:函数![]() 满足
满足![]() ,又
,又![]() .则函数
.则函数![]() 的解析式为 .
的解析式为 .
【解析】由已知![]() ,当
,当![]() 时,原方程化为
时,原方程化为![]() .
.
由等式右边存在极限,![]() 处处可导.
处处可导.
对原方程两边令![]() ,得
,得![]() .
.
令![]() ,
,![]() (
(![]() 为常数).
为常数).
又![]() ,得
,得![]() .
.
7. 用单位立方块搭一个几何体,使它的主视图和俯视图如右图所示,
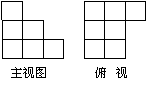 则它的体积的最大值与最小值之差为 .
则它的体积的最大值与最小值之差为 .
【解析】6.体积的最大值为16,体积最小值为10.
8. 已知![]() ,
,![]() ,对任意
,对任意![]() ,经过两点
,经过两点![]() 的直线与一定圆相切,则圆方程为 .
的直线与一定圆相切,则圆方程为 .
【解析】经过两点![]() 的直线方程为
的直线方程为![]() .
.
![]() ,
,![]() .
.
9. 打开“几何画板”软件进行如下操作:
①用画图工具在工作区画一个大小适中的圆C;
②用取点工具分别在圆C上和圆C外各取一个点A、B;
③用构造菜单下对应命令作出线段AB的垂直平分线l;
④作出直线AC.
设直线AC与直线l相交于点P,当点A在圆C上运动时,点P的轨迹是____________.
【解析】双曲线.由图可得,PC—PB=PC—PA=AC,或PB—PC=PA—PC=AC,
从而点P到定点B、C的距离之差的绝对值是定长AC,由双曲线定义即可得.
10.复数![]() ,满足
,满足![]() ,则
,则![]() 与
与![]() 的大小关系是_________.
的大小关系是_________.
【解析】因为![]() ,所以
,所以![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]()
![]()
![]() .
.
11. 已知![]() 的外接圆的圆心
的外接圆的圆心![]() ,
,![]() ,则
,则![]() 的大小关系为______.
的大小关系为______.
【解析】设![]() 的外接圆的半径为
的外接圆的半径为![]() ,
,![]() ,
,![]() ,
,
![]() .
.![]()
![]() ,
,![]() .
.
![]() ,
,![]() .
.
![]()
12. 已知![]() ,则
,则![]() 的值______
的值______
【解析】 ∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() .
.
∴![]() =
=![]()
=![]() .
.
13. 当x=2时,下面这段程序输出的结果是___________.
 |
End Whlie
![]()
![]()
答案:13.
14. 极坐标系中,直线![]() 与曲线
与曲线![]() 相交所得弦长为
.
相交所得弦长为
.
【解析】直线![]() ,为过点
,为过点![]() 且倾斜角为
且倾斜角为![]() 的直线,而曲线
的直线,而曲线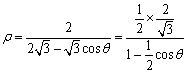 表示的是一个椭圆;建立一个以椭圆的中心为原点的直角坐标系,则椭圆的标准方程为
表示的是一个椭圆;建立一个以椭圆的中心为原点的直角坐标系,则椭圆的标准方程为![]() ,直线的参数方程为
,直线的参数方程为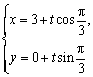 ,代入标准方程,得
,代入标准方程,得![]() ,弦长为
,弦长为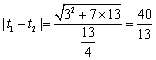 .
.
15. 已知实数![]() 满足
满足![]() ,
,![]() ,则
,则![]() 的取值范围是 .
的取值范围是 .
【解析】由柯西不等式,得![]() ,
,
即![]() .由条件,得
.由条件,得![]() .
.
解得![]() ,当且仅当
,当且仅当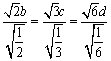 时等号成立.
时等号成立.
代入![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
所以,![]() 的取值范围是
的取值范围是![]() .
.
16. f(x)是定义在(0,+∞)上的非负可导函数,且满足xf‘(x)-f(x)>0,对任意正数a、b,若a<b,则![]() 的大小关系为
.
的大小关系为
.
【解析】设![]() ,则
,则![]() ,故
,故![]() 为增函数,由a<b,
为增函数,由a<b,
有![]() .
.
二、解答题
17. 在数列{an}中,已知,a1=2,an+1+ an+1 an-2 an.对于任意正整数![]() ,
,
(Ⅰ)求数列{an}的通项an的表达式;
(Ⅱ)若 ![]() (
(![]() 为常数,且为整数),求
为常数,且为整数),求![]() 的最小值.
的最小值.
解:(Ⅰ)由题意,对于n∈N*,![]() ,且
,且![]() ,即
,即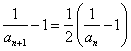 .
.
由 ![]() ,得
,得 ![]() .则数列
.则数列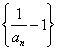 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列.于是
的等比数列.于是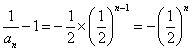 , 即
, 即 ![]() .
.
(Ⅱ)由(Ⅰ),得![]() . 当
. 当![]() 时,因为
时,因为
![]() ,
,
所以![]()
![]()
![]()
![]() .
.
又![]()
![]()
![]() ,故M的最小值为3.
,故M的最小值为3.
18. 设顶点为![]() 的抛物线
的抛物线![]() 交
交![]() 轴正半轴于
轴正半轴于![]() 、
、![]() 两点,交
两点,交![]() 轴正半轴于
轴正半轴于![]() 点,圆
点,圆![]() (圆心为
(圆心为![]() )过
)过![]() 、
、![]() 、
、![]() 三点,恰好与
三点,恰好与![]() 轴相切. 求证:
轴相切. 求证:![]() .
.
解:设![]() 、
、![]() 、
、![]() 三点的坐标为
三点的坐标为![]() ,
,![]() ,
,![]() ,圆
,圆![]() 的圆心坐标为
的圆心坐标为![]() ,
,
由韦达定理,知![]() . 原点
. 原点![]() 到圆D的切线为
到圆D的切线为![]() ,所以
,所以
![]() ,即
,即![]() . 故
. 故![]() .
.
![]() 点坐标为
点坐标为 ![]() . 由(1),
. 由(1),![]() .
.
设![]() 交
交![]() 轴于
轴于![]() ,要证
,要证![]() 与圆
与圆![]() 相切,即证
相切,即证 ![]() .
.
如果![]() ,那么
,那么![]() 与
与![]() 相似,
相似,![]() .
.
所以只需证 ![]() .而
.而 ![]() ,
,![]() ,
,
所以![]() 等价于
等价于 ![]() ,即只需要证
,即只需要证![]() .
.
由![]() ,
,![]() ,所以
,所以![]() 与圆
与圆![]() 相切.
相切.
19. 已知函数![]() 的图象x轴的交点至少有一个在原点右侧.
的图象x轴的交点至少有一个在原点右侧.
(1)求实数m的取值范围;
(2)令t=-m+2,求![]() 的值(其中[t]表示不大于t的最大整数);
的值(其中[t]表示不大于t的最大整数);
(3)对(2)中的t,求函数 的值域.
的值域.
【解析】若m=0 则![]() 符合题意.
符合题意.
若m≠0 ,①m<0时,∵![]() 两根异号,∴必有一个负根.
两根异号,∴必有一个负根.
②m>0时,由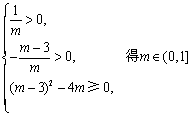 时,方程有两正根.综上得
时,方程有两正根.综上得![]() .
.
(2)∵t=-m+2 ,∴![]() .当t=1时,
.当t=1时,![]() ,当t>1时,
,当t>1时,![]() .
.
(3)当t=1时,![]() ;当t>1时,
;当t>1时,![]() =0,设[t]=n,且t=[t]+a,则
=0,设[t]=n,且t=[t]+a,则![]() .
.
于是 .由函数
.由函数![]() 时是增函数,
时是增函数,
及 .
.
设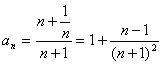 递减,∴
递减,∴![]() .
.
∴![]() .
.
 递减,∴
递减,∴![]() .
.
于是t>1时,![]() 的值域为
的值域为![]() .
.
综上![]() 的值域为
的值域为![]() .
.
20. 已知定理:“若![]() 为常数,
为常数,![]() 满足
满足![]() ,则函数
,则函数![]() 的图象关于点
的图象关于点![]() 中心对称”.设函数
中心对称”.设函数![]() ,定义域为A.
,定义域为A.
(1)试证明![]() 的图象关于点
的图象关于点![]() 成中心对称;
成中心对称;
(2)当![]() 时,求证:
时,求证:![]() ;
;
(3)对于给定的![]() ,设计构造过程:
,设计构造过程:![]()
![]() ,…,
,…,![]() .如果
.如果![]() ,构造过程将继续下去;如果
,构造过程将继续下去;如果![]() ,构造过程将停止.若对任意
,构造过程将停止.若对任意![]() ,构造过程可以无限进行下去,求a的值.
,构造过程可以无限进行下去,求a的值.
【解析】(1)∵![]() ,∴
,∴![]() .
.
由已知定理,得![]() 的图象关于点
的图象关于点![]() 成中心对称.
成中心对称.
(2)先证明![]() 在
在![]() 上是增函数,只要证明
上是增函数,只要证明![]() 在
在![]() 上是增函数.
上是增函数.
设![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上是增函数.
上是增函数.
再由![]() 在
在![]() 上是增函数,得
上是增函数,得
当![]() 时,
时,![]() ,即
,即![]() .
.
(3)∵构造过程可以无限进行下去,∴![]() 对任意
对任意![]() 恒成立.
恒成立.
∴方程![]() 无解,即方程
无解,即方程![]() 无解或有唯一解
无解或有唯一解![]() .
.
∴![]() 或
或 由此得到
由此得到![]() .
.
21. 设A(x1,y1),B(x2,y2)是函数f(x)=![]() 的图象上任意两点,且
的图象上任意两点,且![]() ,已知点M的横坐标为
,已知点M的横坐标为![]() .
.
(1)求证:M点的纵坐标为定值;
(2)若Sn=f(![]() ∈N*,且n≥2,求Sn.
∈N*,且n≥2,求Sn.
(3)已知an= 其中n∈N*.
其中n∈N*.
Tn为数列{an}的前n项和,若Tn<λ(Sn+1+1)对一切n∈N*都成立,试求λ的取值范围.
【解析】(1)证明:∵![]() ∴M是AB的中点.设M点的坐标为(x,y),
∴M是AB的中点.设M点的坐标为(x,y),
由![]() (x1+x2)=x=
(x1+x2)=x=![]() ,得x1+x2=1,则x1=1-x2或x2=1-x1.
,得x1+x2=1,则x1=1-x2或x2=1-x1.
而y=![]() (y1+y2)=
(y1+y2)= ![]() [f(x1)+f(x2)] =
[f(x1)+f(x2)] =![]() (
(![]() +log2
+log2![]()
=![]() (1+log2
(1+log2![]() =
=![]() (1+log2
(1+log2![]()
=![]() (1+log2
(1+log2![]() ∴M点的纵坐标为定值
∴M点的纵坐标为定值![]() .
.
(2)由(1),知x1+x2=1,f(x1)+f(x2)=y1+y2=1,
Sn=f(![]() Sn=f(
Sn=f(![]() ,
,
两式相加,得
2Sn=[f(![]() )+[f(
)+[f(![]() )+…+[f(
)+…+[f(![]() )
)
=![]() ,∴Sn=
,∴Sn=![]() (n≥2,n∈N*).
(n≥2,n∈N*).
(3)当n≥2时,an=![]()
Tn=a1+a2+a3+…+an=![]() [(
[(![]() ]
]
=![]() (
(![]()
由Tn<λ(Sn+1+1),得![]() <λ·
<λ·![]() ∴λ>
∴λ>
∵n+![]() ≥4,当且仅当n=2时等号成立,∴
≥4,当且仅当n=2时等号成立,∴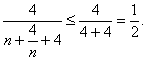
因此λ>![]() ,即λ的取值范围是(
,即λ的取值范围是(![]() +∞).
+∞).
22. 有红色和黑色两个盒子,红色盒中有6张卡片,其中一张标有数字0,2张标有数字1,3张标有数字2;黑色盒中有7张卡片,其中4张标有数字0,1张标有数字1,2张标有数字2.现从红色盒中任意取1张卡片(每张卡片被抽出的可能性相等),黑色盒中任取2张卡片(每张卡片被抽出的可能性相等),共取3张卡片.
(Ⅰ)求取出的3张卡片都标有数字0的概率;
(Ⅱ)求取出的3张卡片数字之积是4的概率;
(Ⅲ)求取出的3张卡片数字之积是0的概率.
【解析】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)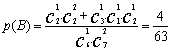 ;
;
(Ⅲ)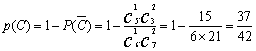 .
.
答:(略).
23. 设函数![]() 的定义域为R,当x<0时
的定义域为R,当x<0时![]() >1,且对任意的实数x,y∈R,有
>1,且对任意的实数x,y∈R,有![]() .
.
(Ⅰ)求![]() ,判断并证明函数
,判断并证明函数![]() 的单调性;
的单调性;
(Ⅱ)数列![]() 满足
满足![]() ,且
,且![]() .
.
①求![]() 通项公式.
通项公式.
②当![]() 时,不等式
时,不等式![]() 对不小于2的正整数恒成立,求x的取值范围.
对不小于2的正整数恒成立,求x的取值范围.
【解析】(Ⅰ)![]() 时,f(x)>1.
时,f(x)>1.
令x=-1,y=0,则f(-1)=f(-1)f(0).∵f(-1)>1 ,∴f(0)=1.
若x>0,则f(x-x)=f(0)=f(x)f(-x).
故![]() ,故x∈R, f(x)>0.
,故x∈R, f(x)>0.
任取x1<x2,![]() ,
,
![]() ,故f(x)在R上减函数.
,故f(x)在R上减函数.
(Ⅱ)①![]() .由f(x)单调性,an+1=an+2 ,
.由f(x)单调性,an+1=an+2 ,
故{an}等差数列,![]() .
.
②![]() .
.
![]()
![]()
∴![]() 是递增数列.
是递增数列.
 当n≥2时,
当n≥2时,![]() ,
,
![]() ,
,
即![]() .
.
而a>1,∴x>1,故x的取值范围(1,+∞).
24. 已知数列![]() 满足
满足 ![]() ,令
,令![]()
![]() ,求证
,求证
(1)数列![]() 是等比数列;
是等比数列;
(2)![]() .
.
解析:(1)![]() .
.![]()
∴![]() =
=![]() ,
,
∵![]() ,∴
,∴ ![]() .
.
∴数列![]() 是等比数列.
是等比数列.
(2)∵ 数列![]() 是等比数列,∴
是等比数列,∴![]() .
.
∵ ![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵
![]() =
=![]()
=![]() ,
,
∴![]()
![]() .
.
25. 已知圆O的方程为![]() 过直线
过直线![]() 上的任意一点P作圆O的切线PA、PB.四边形OABP的面积取得最小时的点P的坐标(m,n)设
上的任意一点P作圆O的切线PA、PB.四边形OABP的面积取得最小时的点P的坐标(m,n)设![]() .
.
(1)求证:当![]() 恒成立;
恒成立;
(2)讨论关于![]() 的方程:
的方程:![]() 根的个数.
根的个数.
解析:(1)![]() =
=![]() .
.
当![]() 取得最小值时
取得最小值时![]() 取得最小,过点O 作
取得最小,过点O 作![]() 垂直于直线
垂直于直线![]() ,交点为
,交点为![]() ,
,
易得![]() ,∴
,∴![]() .∴
.∴![]() .
.
∴![]() ,∴
,∴![]() 在
在![]() 是单调增函数,
是单调增函数,
∴![]()
![]() 对于
对于![]() 恒成立.
恒成立.
(2)方程![]() ,∴
,∴![]() .
.
∵ ![]() ,∴ 方程为
,∴ 方程为![]() .令
.令![]() ,
,
![]() ,当
,当![]() 上为增函数;
上为增函数;
![]() 上为减函数,
上为减函数,
当![]() 时,
时,![]()
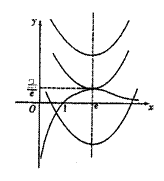
![]() ,
,
∴![]() 、
、![]() 在同一坐标系的大致图象如图所示,
在同一坐标系的大致图象如图所示,
∴①当![]() 时,方程无解.
时,方程无解.
②当![]() 时,方程有一个根.
时,方程有一个根.
③当![]() 时,方程有两个根.
时,方程有两个根.
26. 解不等式![]() .
.
解:(Ⅰ)当x<-2时,得-(2x-1)-(x+2)<4,得![]() ,此不等式无解.
,此不等式无解.
(Ⅱ)当-2![]() x<
x<![]() ,得-(2x-1)+(x+2)<4,得x>-1,
,得-(2x-1)+(x+2)<4,得x>-1,![]() .
.
(Ⅲ)当x![]() 时,得(2x-1)+(x+2)<4,得
时,得(2x-1)+(x+2)<4,得![]() .
.
综上,原不等式的解集为(-1,1).
27. 已知函数![]() 在点P
在点P![]() 处的切线方程为
处的切线方程为![]() ,又
,又![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调区间和极值;
的单调区间和极值;
(3)若函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,求
,求![]() 应满足的条件.
应满足的条件.
解:(1)由题设,知![]() ,
,![]() ,
,![]() ,
,
解得![]() ,所以
,所以![]() .
.
(2)由![]() ,得
,得![]() .由
.由![]() ,得
,得![]() .
.
![]() 的单调增区间是
的单调增区间是![]() ,单调减区间为
,单调减区间为![]() .
.
当![]() 时,
时,![]() 取得极大值0,当
取得极大值0,当![]() 时,
时,![]() 取得极小值
取得极小值![]() .
.
(3)由(2)知,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.因为
上是减函数.因为![]() ,
,
所以![]() ,所以
,所以![]() .
.
此时![]() ,由
,由![]() ,得
,得![]() .
.
所以![]() .
.
综上,![]() .
.
28. 结论:圆C:![]() 与x轴相交于M、N两点,设点P是圆C上任一点,则直线PM、PN斜率的乘积是定值.
与x轴相交于M、N两点,设点P是圆C上任一点,则直线PM、PN斜率的乘积是定值.
(1)写出以上结论在椭圆![]() 中的推广,并加以证明;
中的推广,并加以证明;
(2)将(1)的结论类比到双曲线![]() ,并加以证明.
,并加以证明.
解:(1)设椭圆![]() 与x轴交于M、N两点,设点P是椭圆上任一点,则直线PM、PN斜率的乘积是定值.
与x轴交于M、N两点,设点P是椭圆上任一点,则直线PM、PN斜率的乘积是定值.
证明:由题意![]() ,设
,设![]() ,
,
则![]() ,所以
,所以![]() ,所以
,所以![]() .
.
![]() 是定值.
是定值.
(2)设双曲线![]() 与x轴交于M、N两点,设点P是双曲线上任一点,则直线PM、PN斜率的乘积是定值.
与x轴交于M、N两点,设点P是双曲线上任一点,则直线PM、PN斜率的乘积是定值.
证明:由题意![]() ,设
,设![]() ,
,
则![]() ,所以
,所以![]() ,所以
,所以![]() .
.
![]() 是定值.
是定值.
29. 已知函数![]() 的定义域为R,对任意实数
的定义域为R,对任意实数![]() 满足
满足![]() ,且
,且![]() .
.
(1)求![]() ;
;
(2)试用![]() 表示
表示![]() ;
;
(3)用![]() ,
,![]() 的表达式来表示
的表达式来表示![]() .
.
答案:(1)利用赋值法易得![]() .
.
(2)令![]() ,由条件,得
,由条件,得![]() ,所以
,所以![]() .
.
(3)设![]() ,由条件,得
,由条件,得![]() ,
,
所以 .
.
30. 某保险公司新开设了一项保险业务,若在一年内事件E发生,该公司要赔偿a元,设在一年内E发生的概率为p,为使公司收益的期望值等于a的百分之十,公司应要求顾客交多少保险金
解:设保险公司要求赔偿顾客交x元保险金,若以![]() 表示公司每年的收益额,则
表示公司每年的收益额,则![]() 的分布列为
的分布列为
|
|
|
|
| p | 1-p | p |
![]() 公司每年收益
公司每年收益![]() 的期望值为:E
的期望值为:E![]() =x(1-p)+(x-p)p=x-ap,
=x(1-p)+(x-p)p=x-ap,
要使公司收益的期望值等于a的10%,只需E![]() =0.1a,即x-ap=0.1a,x=(0.1+p)a,
=0.1a,即x-ap=0.1a,x=(0.1+p)a,
![]() 应交的保险金为(0.1+p)a.
应交的保险金为(0.1+p)a.