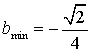高三文科数学第一学期期中考试卷()(3)
一、填空题:(5×14=70)
1.已知全集U=R,集合![]()
2. 等差数列![]() 中,
中,![]() ,那么
,那么![]() 的值是
的值是
3.直线![]() 与直线
与直线![]() 垂直的充要条件是
垂直的充要条件是
4. 复数![]() 的值为
的值为
5.下列函数中,在其定义域内既是奇函数,又是减函数的是
①![]()
![]() ②
② ![]()
![]() ③
③ ![]() ④
④
![]()
6.与直线2x-y-4=0平行且与曲线![]() 相切的直线方程是 .
相切的直线方程是 .
7.函数![]() 的定义域和值域分别是
和
的定义域和值域分别是
和
8.在![]() 中,
中,![]() ,则
,则![]()
9.圆![]() 截直线x-y-5=0所得弦长等于
截直线x-y-5=0所得弦长等于
10. P是椭圆![]() 上的动点, 作PD⊥y轴, D为垂足, 则PD中点的轨迹方程为 .
上的动点, 作PD⊥y轴, D为垂足, 则PD中点的轨迹方程为 .
11.已知双曲线![]() -
-![]() =1的一条准线与抛物线y
=1的一条准线与抛物线y![]() =4x的准线重合,则双曲线的离心率为
=4x的准线重合,则双曲线的离心率为
12.若![]() 是正常数,
是正常数,![]() ,
,![]() ,则
,则![]() ,当且仅当
,当且仅当![]() 时上式取等号. 利用以上结论,可以得到函数
时上式取等号. 利用以上结论,可以得到函数![]() (
(![]() )的最小值为 ,取最小值时
)的最小值为 ,取最小值时![]() 的值为 .
的值为 .
13.一水池有两个进水口,一个出水口,每水口的进出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)

给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水,则一定能确定正确的诊断是 .
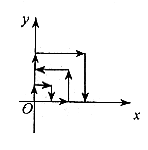 14. 如图,一个粒子在第一象限运动,在第一秒末,它从原点运动到(0,1),接着它按如图所示的x轴、y轴的平行方向来回运动,(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…),且每秒移动一个单位,那么第2008秒末这个粒子所处的位置的坐标为______。
14. 如图,一个粒子在第一象限运动,在第一秒末,它从原点运动到(0,1),接着它按如图所示的x轴、y轴的平行方向来回运动,(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…),且每秒移动一个单位,那么第2008秒末这个粒子所处的位置的坐标为______。
二、解答题:
15.(本小题满分14分)
求满足下列条件曲线的标准方程:
(1)长轴是短轴的3倍且经过点B(0,1)的椭圆方程;
(2)顶点在原点,焦点在x轴上且通径长为6的抛物线方程。
16.(本小题满分14分)
已知向量![]() =(cos
=(cos![]() x,sin
x,sin![]() x),
x),![]() =(
=(![]() ),且x∈[0,
),且x∈[0,![]() ].
].
(1)求![]() ;
;
(2)设函数![]() +
+![]() ,求函数
,求函数![]() 的最值及相应的
的最值及相应的![]() 的值。
的值。
17.(本小题满分14分)
某村计划建造一个室内面积为800m2的矩形蔬菜温室.在温室内,沿左、右两侧与后侧内墙各保留1m宽的通道,沿前侧内墙保留3m宽的空地.当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
18.(本小题满分16分)
设函数![]() (
(![]() ),已知数列
),已知数列![]()
![]()
![]() 是公差为2的等差数列,且
是公差为2的等差数列,且![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)当![]() 时,求证:
时,求证:![]() .
.
19.(本小题满分16分)
(普通班做)已知点M(-2,0),N(2,0),动点P满足条件![]() ,该动点的轨迹为F,
,该动点的轨迹为F,
(1)求F的方程。
(2)若A、B是F上的不同两点,O是坐标原点,求![]() 的最小值。
的最小值。
 |
(免试班做)已知圆O:![]() ,圆C:
,圆C:![]() ,由两圆外一点
,由两圆外一点![]() 引两圆切线PA、PB,切点分别为A、B,满足PA=PB.
引两圆切线PA、PB,切点分别为A、B,满足PA=PB.
(Ⅰ)求实数a、b间满足的等量关系;
(Ⅱ)求切线长PA的最小值;
(Ⅲ)是否存在以P为圆心的圆,使它与圆O相内切
并且与圆C相外切?若存在,求出圆P的方程;
若不存在,说明理由.
20.(本小题满分16分)
(普通班做)
定义在D上的函数![]() ,如果满足:
,如果满足:![]() ,
,![]() 常数
常数![]() ,都有
,都有![]() ≤M成立,则称
≤M成立,则称![]() 是D上的有界函数,其中M称为函数的上界.
是D上的有界函数,其中M称为函数的上界.
(Ⅰ)试判断函数![]() 在[1,3]上是不是有界函数?请给出证明;
在[1,3]上是不是有界函数?请给出证明;
(Ⅱ)若已知质点的运动方程为![]() ,要使在
,要使在![]() 上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
(免试班做)
对于函数![]() ,若存在实数
,若存在实数![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点.
的不动点.
(1)当![]() 时,求
时,求![]() 的不动点;
的不动点;
(2)若对于任何实数![]() ,函数
,函数![]() 恒有两相异的不动点,求实数
恒有两相异的不动点,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若![]() 的图象上
的图象上![]() 、
、![]() 两点的横坐标是函数
两点的横坐标是函数![]() 的不动点,且直线
的不动点,且直线![]() 是线段
是线段![]() 的垂直平分线,求实数
的垂直平分线,求实数![]() 的最小值.
的最小值.
第一学期期中测试数学(文)试卷答案
一、填空题:
1.{xx≤2}
2. 24 3.![]() 4.
4.![]() 5.③ 6.16x-8y+25=0
5.③ 6.16x-8y+25=0
7.![]() ,
,![]() 8. 1 9.
8. 1 9. ![]() 10.
10. ![]() 11.
11. ![]() 12.25,
12.25, ![]()
13.① 14. (16,44)
二、解答题:
15.(1)![]() ,
,![]() ;(2)
;(2)![]()
16.解:(I)由已知条件: ![]() , 得:
, 得:
![]()
![]()
(2)![]()
![]()
![]()
因为:![]() ,所以:
,所以:![]() 所以,只有当:
所以,只有当:![]() 时,
时, ![]()
![]() ,
, ![]()
17.解:设矩形温室的左侧边长为![]() ,后侧边长为
,后侧边长为![]() ,则
,则![]() .
.
∴蔬菜的种植面积![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() (m2),
(m2),
当且仅当![]() ,即
,即![]() 时,
时,![]() m2.
m2.
答:当矩形温室的左侧边长为40m,后侧边长为20m时,蔬菜的种植面积最大,最大种植面积为648 m2.
18.(Ⅰ)![]()
![]()
(Ⅱ)当![]() 时,
时,![]() ,
,
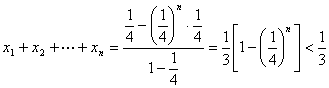
19.(普通班做)(1)F的方程为![]()
![]()
(2)![]()
![]()


(免试班做)
(Ⅰ)连结PO、PC,∵PA=PB,OA=CB=1,
∴PO2=PC2,从而![]()
化简得实数a、b间满足的等量关系为:
![]() .
.
(Ⅱ)由![]() ,得
,得![]()
![]()
![]()
![]()
∴当![]() 时,
时,![]() (Ⅱ)∵圆O和圆C的半径均为1,若存在半径为R圆P,与圆O相内切
(Ⅱ)∵圆O和圆C的半径均为1,若存在半径为R圆P,与圆O相内切
并且与圆C相外切,则有
![]() 且
且 ![]()
于是有:![]() 即
即 ![]()
从而得 ![]()
两边平方,整理得![]()
将![]() 代入上式得:
代入上式得:![]()
故满足条件的实数a、b不存在,∴不存在符合题设条件的圆P.
20.(普通班做)(Ⅰ)∵![]() ,当
,当![]() 时,
时,![]() .
.
∴![]() 在[1,3]上是增函数.
在[1,3]上是增函数.
∴当![]() 时,
时,![]() ≤
≤![]() ≤
≤![]() ,即 -2≤
,即 -2≤![]() ≤26.
≤26.
∴存在常数M=26,使得![]() ,都有
,都有![]() ≤M成立.
≤M成立.
故函数![]() 是[1,3]上的有界函数.
是[1,3]上的有界函数.
(Ⅱ)∵![]() . 由
. 由![]() ≤1,得
≤1,得![]() ≤1
≤1
∴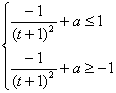
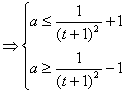
令![]() ,显然
,显然![]() 在
在![]() 上单调递减,
上单调递减,
则当t→+∞时,![]() →1. ∴
→1. ∴![]()
令![]() ,显然
,显然![]() 在
在![]() 上单调递减,
上单调递减,
则当![]() 时,
时,![]() ∴
∴![]()
∴0≤a≤1;
故所求a的取值范围为0≤a≤1.
(免试班做)
解![]()
(1)当![]() 时,
时, ![]()
设![]() 为其不动点,即
为其不动点,即![]()
则![]()
![]() 的不动点是-1,2
的不动点是-1,2
(2)由![]() 得:
得:![]() . 由已知,此方程有相异二实根,
. 由已知,此方程有相异二实根,
![]() 恒成立,即
恒成立,即![]() 即
即![]() 对任意
对任意![]() 恒成立.
恒成立.
![]()
(3)设![]() ,
,
直线![]() 是线段AB的垂直平分线, ∴
是线段AB的垂直平分线, ∴ ![]()
记AB的中点![]() 由(2)知
由(2)知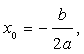
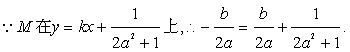
化简得: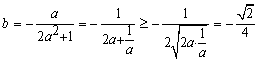
![]() 时,等号成立).
时,等号成立).