高三第一学期期中数学考试卷（理科）(1)
一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中．只有一项是符合题目要求的．）
1、设全集U=R，
，则
=（ ）
A、
B、
C、
D、
2、在△ABC中，“
”是“△ABC为锐角三角形”的（ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既非充分也非必要条件
3、若点
为
的外心，且
，则
的内角
等于（ ）
A．
B．
C．
D．
4、函数
在区间
内单调递增，则
的取值范围是（ ）
A．
B．
C．
D．
5、设
的最小值为（ ）
A．2 B．
C．4 D．
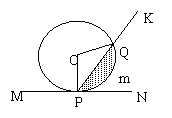
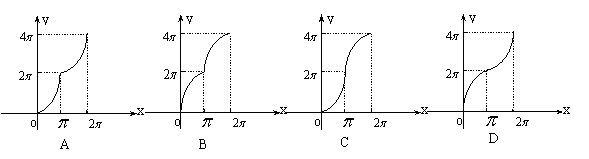6、如图，半径为2的⊙O切直线MN于点P，射线PK从PN出发，绕P点逆
时针旋转到PM，旋转过程中PK交⊙O于点Q，若∠POQ为x，弓形PmQ的面积为S=f(x)，那么f(x)的图象大致是（ ）
7、设
的反函数为
，且
，则
=（ ）
A. -2 B. -1 C. 1 D. 2
8、已知函数
为奇函数，函数
为偶函数，且
，则
（ ）
A．
B．
C．
D．
9、在△ABC中，tanA是第3项为－4、第7项为4的等差数列的公差，tanB是第3项为
，第6项为9的等比数列的公比，则△ABC是（ ）
A．等腰三角形 B．锐角三角形 C．直角三角形 D．钝角三角形
10、设
是函数
的单调递增区间，将的图像按向量
平移得到一个新的函数
的图像，则的单调递减区间必定是（ ）
A．
B．
C．
D．
11、已知
是定义在R上的不恒为零的函数，且对于任意实数
满足：
，考察下列结论：①
；②为偶函数；③数列{
)为等比数列；④数列{
)为等差数列。其中正确的结论是（ ）
A、①②③ B、①③④ C、①②④ D、①③
12、
|
，正实数
、
、
成公差为正数的等差数列，且满足
，若实数
是方程
的一个解，那么下列四个判断：①
；②
；③
；④
中有可能成立的个数为（ ）
A．1 B．2 C．3 D．4
二、填空题（本大题共4小题，每小题4分，共16分，把答案填在题中的横线上）
13、设
是两个互相垂直的单位向量，
的值为
．
14、设数列
的前
．
15、已知
，且函数
在
上具有单调性，则
的取值范围是
．
16、对于函数
：①
，②存在
对任意
恒成立，③存在
使函数
的图象关于
轴对称，④存在两个不同实数
有
其中不正确命题的序号是
．
三、解答题（本大题共6小题，共74分．解答须写出文字说明、证明过程和演算步骤．）
17、（本小题满分12分）设函数
，
（1）求的周期以及单调增区间； （2）若
，求sin2x的值；
（3）在△ABC中，a，b，c分别是角A，B，C的对边，
求b，c的长。
18.（本小题满分12分）锐角三角形ABC中，角A、B、C所对的边分别为a、b、c，
=(a-b,c), 
=(a-c,a+b)，且与共线。
（1）求角B的大小；（2）设
,求y的最大值及此时∠C的大小。
19．（本小题满分12分）设函数
定义域为
，当
时,
,且对于任意的
,都有
（1）求
的值,并证明函数在上是减函数；
（2）记△ABC的三内角A、B、C的对应边分别为a，b，c，若
时，不等式
恒成立，求实数
的取值范围。
20．（本小题满分12分）设函数
.对于正项数列
，其前
（1）求实数 （2）求数列的通项公式
（3）若
大小，并说明理由。
21．（本小题满分12分）已知函数
为常数）是实数集R上的奇函数，函数
是区间[－1，1]上的减函数.
（1）求a的值； （2）若
上恒成立，求
的取值范围；
（3）讨论关于
的根的个数.
22. （本小题满分14分）在数列
中，其中
⑴求数列的通项公式；
⑵设
，证明：当
时，
.
南昌市重点中学2007－2008学年度第一学期期中考试卷
高三数学（理科）参考答案
一、选择题（本大题共12小题，每小题5分，共60分．）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | B | D | A | B | C | A | C | B | D | B | C |
二、填空题（本大题共4小题，每小题4分，共16分，）
13. 2
14. 
15. 
16. ①②③④
三、解答题（本大题共6小题，共74分．解答须写出文字说明、证明过程和演算步骤．）
17、（本小题满分12分）设函数，
（1）求的周期以及单调增区间； （2）若，求sin2x的值；
（3）在△ABC中，a，b，c分别是角A，B，C的对边， 求b，c的长。
解：（1）
∴的最小正周期为π
单调增区间为 
（2）
∴
∵
（3）
∵
由
，∴bc=2。又b+c=3（b>c），∴
18.（本小题满分12分）锐角三角形ABC中，角A、B、C所对的边分别为a、b、c，=(a-b,c), =(a-c,a+b)，且与共线。（1）求角B的大小；
（2）设,求y的最大值及此时∠C的大小。
解：（1）∵
与
共线，
∴(a-b)(a+b)-c(a-c)=0, ∴
.
∵
（2）∵
∴当
，即
时，y取最大值2
19．（本小题满分12分）设函数定义域为，当时,,且对于任意的,都有
（1）求的值,并证明函数在上是减函数；
（2）记△ABC的三内角A、B、C的对应边分别为a，b，c，若时，不等式恒成立，求实数的取值范围。
解：(1) 
,且当时，，所以
当
时，
，
，
， 
对于
，
，设
，
则
又，所以
，
，
，
即 
，故函数在上是减函数。
（2）
上单调递减，且
所以
20．（本小题满分12分）设函数
.对于正项数列，其前
（1）求实数 （2）求数列的通项公式
（3）若大小，并说明理由。
解：（1）∵
不论
为何实数恒有 
即对
∴
（2）∵
∴
∴
∵a
>0 ∴
∴
是首项为a，公差为2的等数列
由
∴
∴
（3）∵
∴
21．（本小题满分12分）已知函数为常数）是实数集R上的奇函数，函数是区间[－1，1]上的减函数.
（1）求a的值；
（2）若上恒成立，求的取值范围；
（3）讨论关于的根的个数.
解：（1）
是奇函数，则
恒成立.
即
（2）又
在[－1，1]上单调递减，
令
则
.
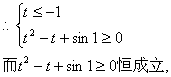
（3）由（I）知
令
，
，
当
上为增函数；
|
上为减函数，
当
时，
而
，
、
在同一坐标系的大致图象如图所示，
∴①当
时，方程无解.
②当
时，方程有一个根.
③当
时，方程有两个根.
22. （本小题满分14分）在数列中，其中
⑴求数列的通项公式；
⑵设，证明：当时，.
⑴解:设 
，
即
故
∴
又
，故存在
是等比数列
所以，
∴
，
⑵证明：由⑴得
∵ 
∴
现证
.
当
，
故
时不等式成立
当
得
，且由
，∴