![]() 必修1
第1章 集 合
必修1
第1章 集 合
§1.1 集合的含义及其表示
重难点:集合的含义与表示方法,用集合语言表达数学对象或数学内容;区别元素与集合等概念及其符号表示;用集合语言(描述法)表达数学对象或数学内容;集合表示法的恰当选择.
考纲要求:①了解集合的含义、元素与集合的“属于”关系;
②能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.
经典例题:若x∈R,则{3,x,x2-2x}中的元素x应满足什么条件?
当堂练习:
1.下面给出的四类对象中,构成集合的是( )
A.某班个子较高的同学 B.长寿的人 C.![]() 的近似值 D.倒数等于它本身的数
的近似值 D.倒数等于它本身的数
2.下面四个命题正确的是( )
A.10以内的质数集合是{0,3,5,7} B.由1,2,3组成的集合可表示为{1,2,3}或{3,2,1}
C.方程![]() 的解集是{1,1} D.0与{0}表示同一个集合
的解集是{1,1} D.0与{0}表示同一个集合
3. 下面四个命题: (1)集合N中最小的数是1; (2)若 -a![]() Z,则a
Z,则a![]() Z;
Z;
(3)所有的正实数组成集合R+;(4)由很小的数可组成集合A;
其中正确的命题有( )个
A.1 B.2 C.3 D.4
4.下面四个命题: (1)零属于空集; (2)方程x2-3x+5=0的解集是空集;
(3)方程x2-6x+9=0的解集是单元集; (4)不等式 2 x-6>0的解集是无限集;
其中正确的命题有( )个
A.1 B.2 C.3 D.4
5. 平面直角坐标系内所有第二象限的点组成的集合是( )
A. {x,y且![]() }
B. {(x,y)
}
B. {(x,y)![]() }
}
C. {(x,y) ![]() }
D. {x,y且
}
D. {x,y且![]() }
}
6.用符号![]() 或
或![]() 填空:
填空:
0__________{0}, a__________{a}, ![]() __________Q,
__________Q, ![]() __________Z,-1__________R, 0__________N, 0
__________Z,-1__________R, 0__________N, 0
![]() .
.
7.由所有偶数组成的集合可表示为{![]() }.
}.
8.用列举法表示集合D={![]() }为
.
}为
.
9.当a满足
时, 集合A={![]() }表示单元集.
}表示单元集.
10.对于集合A={2,4,6},若a![]() A,则6-a
A,则6-a![]() A,那么a的值是__________.
A,那么a的值是__________.
11.数集{0,1,x2-x}中的x不能取哪些数值?
12.已知集合A={x![]() N
N![]()
![]() N },试用列举法表示集合A.
N },试用列举法表示集合A.
13.已知集合A={![]() }.
}.
(1)若A中只有一个元素,求a的值; (2)若A中至多有一个元素,求a的取值范围.
14.由实数构成的集合A满足条件:若a![]() A, a
A, a![]() 1,则
1,则![]() ,证明:
,证明:
(1)若2![]() A,则集合A必还有另外两个元素,并求出这两个元素;
A,则集合A必还有另外两个元素,并求出这两个元素;
(2)非空集合A中至少有三个不同的元素。
![]() 必修1
§1.2 子集、全集、补集
必修1
§1.2 子集、全集、补集
重难点:子集、真子集的概念;元素与子集,属于与包含间的区别;空集是任何非空集合的真子集的理解;补集的概念及其有关运算.
考纲要求:①理解集合之间包含与相等的含义,能识别给定集合的子集;
②在具体情景中,了解全集与空集的含义;
③理解在给定集合中一个子集的补集的含义,会求给定子集的补集.
经典例题:已知A={xx=8m+14n,m、n∈Z},B={xx=2k,k∈Z},问:
(1)数2与集合A的关系如何?
(2)集合A与集合B的关系如何?
当堂练习:
1.下列四个命题:①![]() ={0};②空集没有子集;③任何一个集合必有两个或两个以上的子集;④空集是任何一个集合的子集.其中正确的有( )
={0};②空集没有子集;③任何一个集合必有两个或两个以上的子集;④空集是任何一个集合的子集.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
2.若M={x|x>1},N={x|x≥a},且N![]() M,则( )
M,则( )
A.a>1 B.a≥1 C.a<1 D.a≤1
3.设U为全集,集合M、N![]() U,且M
U,且M![]() N,则下列各式成立的是( )
N,则下列各式成立的是( )
A.![]() u M
u M![]()
![]() u N B.
u N B.![]() u M
u M![]() M
M
C.![]() u M
u M![]()
![]() u N D.
u N D.![]() u M
u M![]() N
N
4. 已知全集U={x|-2≤x≤1},A={x|-2<x<1 =,B={x|x2+x-2=0},C={x|-2≤x<1 =,则( )
A.C![]() A B.C
A B.C![]()
![]() u A
u A
C.![]() u B=C D.
u B=C D.![]() u A=B
u A=B
5.已知全集U={0,1,2,3}且![]() u A={2},则集合A的真子集共有( )
u A={2},则集合A的真子集共有( )
A.3个 B.5个 C.8个 D.7个
6.若A![]() B,A
B,A![]() C,B={0,1,2,3},C={0,2,4,8},则满足上述条件的集合A为________.
C,B={0,1,2,3},C={0,2,4,8},则满足上述条件的集合A为________.
7.如果M={x|x=a2+1,a![]() N*},P={y|y=b2-2b+2,b
N*},P={y|y=b2-2b+2,b![]() N+},则M和P的关系为M_________P.
N+},则M和P的关系为M_________P.
8.设集合M={1,2,3,4,5,6},A![]() M,A不是空集,且满足:a
M,A不是空集,且满足:a![]() A,则6-a
A,则6-a![]() A,则满足条件的集合A共有_____________个.
A,则满足条件的集合A共有_____________个.
9.已知集合A={![]() },
}, ![]() u A={
u A={![]() },
},![]() u B={
u B={![]() },则集合B=
.
},则集合B=
.
10.集合A={xx2+x-6=0},B={xmx+1=0},若B![]() A,则实数m的值是
.
A,则实数m的值是
.
11.判断下列集合之间的关系:
(1)A={三角形},B={等腰三角形},C={等边三角形};
(2)A={![]() },B={
},B={![]() },C={
},C={![]() };
};
(3)A={![]() },B={
},B={![]() },C={
},C={![]() };
};
(4)![]()
12. 已知集合![]() ,且
,且![]() {负实数},求实数p的取值范围.
{负实数},求实数p的取值范围.
13..已知全集U={1,2,4,6,8,12},集合A={8,x,y,z},集合B={1,xy,yz,2x},其中![]() ,若A=B,
,若A=B,
求![]() u A..
u A..
14.已知全集U={1,2,3,4,5},A={x![]() Ux2-5qx+4=0,q
Ux2-5qx+4=0,q![]() R}.
R}.
(1)若![]() u A=U,求q的取值范围;
u A=U,求q的取值范围;
(2)若![]() u A中有四个元素,求
u A中有四个元素,求![]() u A和q的值;
u A和q的值;
(3)若A中仅有两个元素,求![]() u A和q的值.
u A和q的值.
![]() 必修1
§1.3 交集、并集
必修1
§1.3 交集、并集
重难点:并集、交集的概念及其符号之间的区别与联系.
考纲要求:①理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集;
②能使用韦恩图(Venn)表达集合的关系及运算.
经典例题:已知集合A=![]() B=
B=![]() 且A
且A![]() B=B,求实数a的取值范围.
B=B,求实数a的取值范围.
当堂练习:
1.已知集合![]() ,则
,则![]() 的值为 ( ).
的值为 ( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设集合A={(x,y)|4x+y=6},B={(x,y)|3x+2y=7},则满足C![]() A∩B的集合C的个数是( ).
A∩B的集合C的个数是( ).
A.0 B.1 C.2 D.3
3.已知集合![]()
![]() ,
,
![]() ,则实数a的取值范围是( ).
,则实数a的取值范围是( ).
![]()
![]()
4.设全集U=R,集合![]() 的解集是( ).
的解集是( ).
A.![]() B.
B. ![]() ∩(
∩(![]() u N) C.
u N) C.
![]() ∪(
∪(![]() u N) D.
u N) D.![]()
5.有关集合的性质:(1) ![]() u(A
u(A![]() B)=(
B)=(![]() u A)∪(
u A)∪(![]() u B); (2)
u B); (2)![]() u(A
u(A![]() B)=(
B)=(![]() u A)
u A)![]() (
(![]() u B)
u B)
(3) A![]() (
(![]() uA)=U (4) A
uA)=U (4) A ![]() (
(![]() uA)=
uA)=![]() 其中正确的个数有( )个.
其中正确的个数有( )个.
A.1 B. 2 C.3 D.4
6.已知集合M={x|-1≤x<2=,N={x|x—a≤0},若M∩N≠![]() ,则a的取值范围是
.
,则a的取值范围是
.
7.已知集合A={x|y=x2-2x-2,x∈R},B={y|y=x2-2x+2,x∈R},则A∩B= .
8.已知全集![]() (
(![]() u B)
u B)![]()
![]() u A)
u A)![]() ,
, ![]()
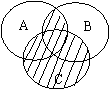 则A= ,B=
.
则A= ,B=
.
9.表示图形中的阴影部分 .
10.在直角坐标系中,已知点集A=![]() ,B=
,B=![]() ,则
,则
(![]() uA)
uA) ![]() B=
.
B=
.
11.已知集合M=![]() ,求实数a的的值.
,求实数a的的值.
12.已知集合![]()
![]() =
=![]() ,求实数b,c,m的值.
,求实数b,c,m的值.
13. 已知A![]() B={3}, (
B={3}, (![]() uA)∩B={4,6,8}, A∩(
uA)∩B={4,6,8}, A∩(![]() uB)={1,5},(
uB)={1,5},(![]() u A)∪(
u A)∪(![]() uB)={
uB)={![]() },试求
},试求![]() u(A∪B),A,B.
u(A∪B),A,B.
14.已知集合A=![]() ,B=
,B=![]() ,且A∪B=A,试求a的取值范围.
,且A∪B=A,试求a的取值范围.
![]() 必修1
第1章 集 合
必修1
第1章 集 合
§1.4 单元测试
1.设A={xx≤4},a=![]() ,则下列结论中正确的是( )
,则下列结论中正确的是( )
![]()
![]() (A){a} A (B)a
(A){a} A (B)a![]() A (C){a}∈A (D)a
A (C){a}∈A (D)a![]() A
A
2.若{1,2} A![]() {1,2,3,4,5},则集合A的个数是( )
{1,2,3,4,5},则集合A的个数是( )
(A)8 (B)7 (C)4 (D)3
3.下面表示同一集合的是( )
(A)M={(1,2)},N={(2,1)} (B)M={1,2},N={(1,2)}
(C)M=![]() ,N={
,N={![]() }
(D)M={x
}
(D)M={x![]() ,N={1}
,N={1}
4.若P![]() U,Q
U,Q![]() U,且x∈CU(P∩Q),则( )
U,且x∈CU(P∩Q),则( )
(A)x![]() P且x
P且x![]() Q (B)x
Q (B)x![]() P或x
P或x![]() Q (C)x∈CU(P∪Q) (D)x∈CUP
Q (C)x∈CU(P∪Q) (D)x∈CUP
5. 若M![]() U,N
U,N![]() U,且M
U,且M![]() N,则( )
N,则( )
(A)M∩N=N (B)M∪N=M (C)CUN![]() CUM (D)CUM
CUM (D)CUM![]() CUN
CUN
6.已知集合M={yy=-x2+1,x∈R},N={yy=x2,x∈R},全集I=R,则M∪N等于( )
(A){(x,y)x=![]() (B){(x,y)x
(B){(x,y)x![]()
(C){yy≤0,或y≥1} (D){yy<0, 或y>1}
7.50名学生参加跳远和铅球两项测试,跳远和铅球测试成绩分别及格40人和31人,两项测试均不及格的有4人,则两项测试成绩都及格的人数是( )
(A)35 (B)25 (C)28 (D)15
8.设x,y![]() R,A=
R,A=![]() ,B=
,B= ![]() ,则A、B间的关系为( )
,则A、B间的关系为( )
(A)A![]() B (B)B
B (B)B![]() A (C)A=B (D)A∩B=
A (C)A=B (D)A∩B=![]()
9. 设全集为R,若M=![]() ,N=
,N= ![]() ,则(CUM)∪(CUN)是( )
,则(CUM)∪(CUN)是( )
(A)![]() (B)
(B) ![]() (C)
(C)![]() (D)
(D) ![]()
10.已知集合![]() ,若
,若![]() 则
则![]() 与集合
与集合![]() 的关系是
( )
的关系是
( )
(A)![]()
![]() 但
但![]() (B)
(B)![]()
![]() 但
但![]() (C)
(C)![]()
![]() 且
且![]() (D)
(D)![]()
![]() 且
且![]()
 11.集合U,M,N,P如图所示,则图中阴影部分所表示的集合是( )
11.集合U,M,N,P如图所示,则图中阴影部分所表示的集合是( )
(A)M∩(N∪P) (B)M∩CU(N∪P)
(C)M∪CU(N∩P) (D)M∪CU(N∪P)
12.设I为全集,A![]() I,B A,则下列结论错误的是( )
I,B A,则下列结论错误的是( )
(A)CIA ![]() CIB (B)A∩B=B (C)A∩CIB =
CIB (B)A∩B=B (C)A∩CIB =![]() (D) CIA∩B=
(D) CIA∩B=![]()
13.已知x∈{1,2,x2},则实数x=__________.
14.已知集合M={a,0},N={1,2},且M∩N={1},那么M∪N的真子集有 个.
15.已知A={-1,2,3,4};B={yy=x2-2x+2,x∈A},若用列举法表示集合B,则B= .
16.设![]() ,
,![]() 与
与![]() 是
是![]() 的子集,若
的子集,若![]() ,则称
,则称![]() 为一个“理
为一个“理
想配集”,那么符合此条件的“理想配集”的个数是 .(规定![]() 与
与![]() 是两个不同的
是两个不同的
“理想配集”)
17.已知全集U={0,1,2,…,9},若(CUA)∩(CUB)={0,4,5},A∩(CUB)={1,2,8},A∩B={9},
试求A∪B.
18.设全集U=R,集合A=![]() ,B=
,B=![]() ,试求CUB, A∪B, A∩B,A∩(CUB),
( CU A) ∩(CUB).
,试求CUB, A∪B, A∩B,A∩(CUB),
( CU A) ∩(CUB).
19.设集合A={x2x2+3px+2=0};B={x2x2+x+q=0},其中p,q,x∈R,当A∩B=![]() 时,求p的值
时,求p的值
和A∪B.
20.设集合A=![]() ,B=
,B=![]() ,问:
,问:
(1) a为何值时,集合A∩B有两个元素;
(2) a为何值时,集合A∩B至多有一个元素.
21.已知集合A=![]() ,B=
,B=![]() ,其中
,其中![]() 均为正整数,且
均为正整数,且![]() ,A∩B={a1,a4},
a1+a4=10, A∪B的所有元素之和为124,求集合A和B.
,A∩B={a1,a4},
a1+a4=10, A∪B的所有元素之和为124,求集合A和B.
22.已知集合A={xx2-3x+2=0},B={xx2-ax+3a-5},若A∩B=B,求实数a的值.
![]() 必修1
第2章 函数概念与基本初等函数Ⅰ
必修1
第2章 函数概念与基本初等函数Ⅰ
§2.1.1 函数的概念和图象
重难点:在对应的基础上理解函数的概念并能理解符号“y=f(x)”的含义,掌握函数定义域与值域的求法; 函数的三种不同表示的相互间转化,函数的解析式的表示,理解和表示分段函数;函数的作图及如何选点作图,映射的概念的理解.
考纲要求:①了解构成函数的要素,会求一些简单函数的定义域和值域;
②在实际情境中,会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数;
③了解简单的分段函数,并能简单应用;
经典例题:设函数f(x)的定义域为[0,1],求下列函数的定义域:
(1)H(x)=f(x2+1);
(2)G(x)=f(x+m)+f(x-m)(m>0).
当堂练习:
1. 下列四组函数中,表示同一函数的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.函数![]() 的图象与直线
的图象与直线![]() 交点的个数为( )
交点的个数为( )
A.必有一个 B.1个或2个 C.至多一个 D.可能2个以上
3.已知函数![]() ,则函数
,则函数![]() 的定义域是( )
的定义域是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.函数![]() 的值域是( )
的值域是( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
 5.对某种产品市场产销量情况如图所示,其中:
5.对某种产品市场产销量情况如图所示,其中:![]() 表示产品各年年产量的变化规律;
表示产品各年年产量的变化规律;![]() 表示产品各年的销售情况.下列叙述: ( )
表示产品各年的销售情况.下列叙述: ( )
(1)产品产量、销售量均以直线上升,仍可按原生产计划进行下去;
(2)产品已经出现了供大于求的情况,价格将趋跌;
(3)产品的库存积压将越来越严重,应压缩产量或扩大销售量;
(4)产品的产、销情况均以一定的年增长率递增.你认为较合理的是( )
A.(1),(2),(3) B.(1),(3),(4) C.(2),(4) D.(2),(3)
6.在对应法则![]() 中,若
中,若![]() ,则
,则![]() ,
, ![]() 6.
6.
7.函数![]() 对任何
对任何![]() 恒有
恒有![]() ,已知
,已知![]() ,则
,则![]() .
.
8.规定记号“![]() ”表示一种运算,即
”表示一种运算,即![]() . 若
. 若![]() ,则函数
,则函数![]() 的值域是___________.
的值域是___________.
9.已知二次函数f(x)同时满足条件: (1) 对称轴是x=1; (2) f(x)的最大值为15;(3) f(x)的两根立方和等于17.则f(x)的解析式是 .
10.函数![]() 的值域是
.
的值域是
.
11. 求下列函数的定义域 : (1)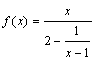 (2)
(2)![]()
12.求函数![]() 的值域.
的值域.
13.已知f(x)=x2+4x+3,求f(x)在区间[t,t+1]上的最小值g(t)和最大值h(t).

14.在边长为2的正方形ABCD的边上有动点M,从点B开始,沿折线BCDA向A点运动,设M点运动的距离为x,△ABM的面积为S.
(1)求函数S=的解析式、定义域和值域;
(2)求f[f(3)]的值.
![]() 必修1
第2章 函数概念与基本初等函数Ⅰ
必修1
第2章 函数概念与基本初等函数Ⅰ
§2.1.2 函数的简单性质
重难点:领会函数单调性的实质,明确单调性是一个局部概念,并能利用函数单调性的定义证明具体函数的单调性,领会函数最值的实质,明确它是一个整体概念,学会利用函数的单调性求最值;函数奇偶性概念及函数奇偶性的判定;函数奇偶性与单调性的综合应用和抽象函数的奇偶性、单调性的理解和应用;了解映射概念的理解并能区别函数和映射.
考纲要求:①理解函数的单调性、最大(小)值及其几何意义;结合具体函数,了解函数奇偶性的含义;并了解映射的概念;
②会运用函数图像理解和研究函数的性质.
经典例题:定义在区间(-∞,+∞)上的奇函数f(x)为增函数,偶函数g(x)在[0,+∞ )上图象与f(x)的图象重合.设a>b>0,给出下列不等式,其中成立的是
① f(b)-f(-a)>g(a)-g(-b) ②f(b)-f(-a)<g(a)-g(-b)
③f(a)-f(-b)>g(b)-g(-a) ④f(a)-f(-b)<g(b)-g(-a)
A.①④ B.②③ C.①③ D.②④
当堂练习:
1.已知函数f(x)=2x2-mx+3,当![]() 时是增函数,当
时是增函数,当![]() 时是减函数,则f(1)等于
( )
时是减函数,则f(1)等于
( )
A.-3 B.13 C.7 D.含有m的变量
2.函数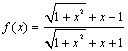 是( )
是( )
A. 非奇非偶函数 B.既不是奇函数,又不是偶函数奇函数 C. 偶函数 D. 奇函数
3.已知函数(1)![]() , (2)
, (2)![]() ,(3)
,(3)![]()
(4)![]() ,其中是偶函数的有( )个
,其中是偶函数的有( )个
A.1 B.2 C.3 D.4
4.奇函数y=f(x)(x≠0),当x∈(0,+∞)时,f(x)=x-1,则函数f(x-1)的图象为 ( )
5.已知映射f:A![]() B,其中集合A={-3,-2,-1,1,2,3,4},集合B中的元素都是A中元素在映射f下的象,且对任意的
B,其中集合A={-3,-2,-1,1,2,3,4},集合B中的元素都是A中元素在映射f下的象,且对任意的![]() ,在B中和它对应的元素是
,在B中和它对应的元素是![]() ,则集合B中元素的个数是( )
,则集合B中元素的个数是( )
A.4 B.5 C.6 D.7
6.函数![]() 在区间[0, 1]上的最大值g(t)是 .
在区间[0, 1]上的最大值g(t)是 .
7. 已知函数f(x)在区间![]() 上是减函数,则
上是减函数,则![]() 与
与![]() 的大小关系是 .
的大小关系是 .
8.已知f(x)是定义域为R的偶函数,当x<0时, f(x)是增函数,若x1<0,x2>0,且![]() ,则
,则![]() 和
和![]() 的大小关系是
.
的大小关系是
.
9.如果函数y=f(x+1)是偶函数,那么函数y=f(x)的图象关于_________对称.
10.点(x,y)在映射f作用下的对应点是![]() ,若点A在f作用下的对应点是B(2,0),则点A坐标是
.
,若点A在f作用下的对应点是B(2,0),则点A坐标是
.
13. 已知函数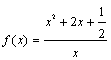 ,其中
,其中![]() ,(1)试判断它的单调性;(2)试求它的最小值.
,(1)试判断它的单调性;(2)试求它的最小值.
14.已知函数![]() ,常数
,常数![]() 。
。
(1)设![]() ,证明:函数
,证明:函数![]() 在
在![]() 上单调递增;
上单调递增;
(2)设![]() 且
且![]() 的定义域和值域都是
的定义域和值域都是![]() ,求
,求![]() 的最大值.
的最大值.
13.(1)设f(x)的定义域为R的函数,求证: ![]() 是偶函数;
是偶函数;
![]() 是奇函数.
是奇函数.
(2)利用上述结论,你能把函数![]() 表示成一个偶函数与一个奇函数之和的形式.
表示成一个偶函数与一个奇函数之和的形式.
14. 在集合R上的映射:![]() ,
,![]() .
.
(1)试求映射![]() 的解析式;
的解析式;
(2)分别求函数f1(x)和f2(z)的单调区间;
(3) 求函数f(x)的单调区间.
![]() 必修1
第2章 函数概念与基本初等函数Ⅰ
必修1
第2章 函数概念与基本初等函数Ⅰ
§2.1.3单元测试
1. 设集合P=![]() ,Q=
,Q=![]() ,由以下列对应f中不能构成A到B的映射的是 ( )A.
,由以下列对应f中不能构成A到B的映射的是 ( )A.![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
2.下列四个函数: (1)y=x+1;
(2)y=x+1; (3)y=x2-1; (4)y=![]() ,其中定义域与值域相同的是( ) A.(1)(2)
B.(1)(2)(3) C.2)(3)
D.(2)(3)(4)
,其中定义域与值域相同的是( ) A.(1)(2)
B.(1)(2)(3) C.2)(3)
D.(2)(3)(4)
3.已知函数![]() ,若
,若![]() ,则
,则![]() 的值为( )
的值为( )
A.10 B. -10 C.-14 D.无法确定
4.设函数![]() ,则
,则![]() 的值为( )
的值为( )
A.a B.b C.a、b中较小的数 D.a、b中较大的数
5.已知矩形的周长为1,它的面积S与矩形的长x之间的函数关系中,定义域为( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6.已知函数y=x2-2x+3在[0,a](a>0)上最大值是3,最小值是2,则实数a的取值范围是( )
A.0<a<1
B.0<a![]() 2
C.
2
C.![]() a
a![]() 2
D. 0
2
D. 0![]() a
a![]() 2
2
7.已知函数![]() 是R上的偶函数,且在(-∞,
是R上的偶函数,且在(-∞,![]() 上是减函数,若
上是减函数,若![]() ,则实数a的取值范围是( )
,则实数a的取值范围是( )
A.a≤2 B.a≤-2或a≥2 C.a≥-2 D.-2≤a≤2
8.已知奇函数![]() 的定义域为
的定义域为![]() ,且对任意正实数
,且对任意正实数![]() ,恒有
,恒有![]() ,则一定有( )
,则一定有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.已知函数![]() 的定义域为A,函数y=f(f(x))的定义域为B,则( )
的定义域为A,函数y=f(f(x))的定义域为B,则( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
10.已知函数y=f(x)在R上为奇函数,且当x![]() 0时,f(x)=x2-2x,则f(x)在
0时,f(x)=x2-2x,则f(x)在![]() 时的解析式是( )
时的解析式是( )
A. f(x)=x2-2x B. f(x)=x2+2x C. f(x)= -x2+2x D. f(x)= -x2-2x
11.已知二次函数y=f(x)的图象对称轴是![]() ,它在[a,b]上的值域是
[f(b),f(a)],则 ( )A.
,它在[a,b]上的值域是
[f(b),f(a)],则 ( )A.
![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.如果奇函数y=f(x)在区间[3,7]上是增函数,且最小值为5,则在区间[-7,-3]上( )
A.增函数且有最小值-5 B. 增函数且有最大值-5 C.减函数且有最小值-5 D.减函数且有最大值-5
13.已知函数![]() ,则
,则![]() .
.
14. 设f(x)=2x+3,g(x+2)=f(x-1),则g(x)= .
15.定义域为![]() 上的函数f(x)是奇函数,则a=
.
上的函数f(x)是奇函数,则a=
.
16.设![]() ,则
,则![]() .
.
17.作出函数![]() 的图象,并利用图象回答下列问题:
的图象,并利用图象回答下列问题:
(1)函数在R上的单调区间; (2)函数在[0,4]上的值域.
18.定义在R上的函数f(x)满足:如果对任意x1,x2∈R,都有f(![]() )≤
)≤![]() [f(x1)+f(x2)],则称函数f(x)是R上的凹函数.已知函数f(x)=ax2+x(a∈R且a≠0),求证:当a>0时,函数f(x)是凹函数;
[f(x1)+f(x2)],则称函数f(x)是R上的凹函数.已知函数f(x)=ax2+x(a∈R且a≠0),求证:当a>0时,函数f(x)是凹函数;
19.定义在(-1,1)上的函数f(x)满足:对任意x、y∈(-1,1)都有f(x)+f(y)=f(![]() ).
).
(1)求证:函数f(x)是奇函数;
(2)如果当x∈(-1,0)时,有f(x)>0,求证:f(x)在(-1,1)上是单调递减函数;
20.记函数f(x)的定义域为D,若存在x0∈D,使f(x0)=x0成立,则称以(x0,y0)为坐标的点是函数f(x)的图象上的“稳定点”.
(1)若函数f(x)=![]() 的图象上有且只有两个相异的“稳定点”,试求实数a的取值范围;
的图象上有且只有两个相异的“稳定点”,试求实数a的取值范围;
(2)已知定义在实数集R上的奇函数f(x)存在有限个“稳定点”,求证:f(x)必有奇数个“稳定点”.
![]() 必修1
第2章 函数概念与基本初等函数Ⅰ
必修1
第2章 函数概念与基本初等函数Ⅰ
§2.2指数函数
重难点:对分数指数幂的含义的理解,学会根式与分数指数幂的互化并掌握有理指数幂的运算性质;指数函数的性质的理解与应用,能将讨论复杂函数的单调性、奇偶性问题转化为讨论比较简单的函数的有关问题.
考纲要求:①了解指数函数模型的实际背景;
②理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算;
③理解指数函数的概念,并理解指数函数的单调性与函数图像通过的特殊点;
④知道指数函数是一类重要的函数模型.
经典例题:求函数y=3![]() 的单调区间和值域.
的单调区间和值域.
当堂练习:
1.数![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.要使代数式![]() 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.一切实数
D.一切实数
3.下列函数中,图象与函数y=4x的图象关于y轴对称的是( )
A.y=-4x B.y=4-x C.y=-4-x D.y=4x+4-x
4.把函数y=f(x)的图象向左、向下分别平移2个单位长度,得到函数![]() 的图象,则( )
的图象,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.设函数![]() ,f(2)=4,则( )
,f(2)=4,则( )
A.f(-2)>f(-1) B.f(-1)>f(-2) C.f(1)>f(2) D.f(-2)>f(2)
6.计算.![]() .
.
7.设![]() ,求
,求![]() .
.
8.已知![]() 是奇函数,则
是奇函数,则![]() =
.
=
.
9.函数![]() 的图象恒过定点
.
的图象恒过定点
.
10.若函数![]() 的图象不经过第二象限,则
的图象不经过第二象限,则![]() 满足的条件是
.
满足的条件是
.
11.先化简,再求值: (1)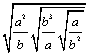 ,其中
,其中![]() ;
;
(2) ![]() ,其中
,其中![]() .
.
12.(1)已知x![]() [-3,2],求f(x)=
[-3,2],求f(x)=![]() 的最小值与最大值.
的最小值与最大值.
(2)已知函数![]() 在[0,2]上有最大值8,求正数a的值.
在[0,2]上有最大值8,求正数a的值.
(3)已知函数![]() 在区间[-1,1]上的最大值是14,求a的值.
在区间[-1,1]上的最大值是14,求a的值.
13.求下列函数的单调区间及值域:
(1) ![]() ;
(2)
;
(2)![]() ; (3)求函数
; (3)求函数![]() 的递增区间.
的递增区间.
14.已知![]()
(1)证明函数f(x)在![]() 上为增函数;(2)证明方程
上为增函数;(2)证明方程![]() 没有负数解.
没有负数解.
![]() 必修1
第2章 函数概念与基本初等函数Ⅰ
必修1
第2章 函数概念与基本初等函数Ⅰ
§2.3对数函数
重难点:理解并掌握对数的概念以及对数式和指数式的相互转化,能应用对数运算性质及换底公式灵活地求值、化简;理解对数函数的定义、图象和性质,能利用对数函数单调性比较同底对数大小,了解对数函数的特性以及函数的通性在解决有关问题中的灵活应用.
考纲要求:①理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用;
②理解对数函数的概念;理解对数函数的单调性,掌握函数图像通过的特殊点;
③知道对数函数是一类重要的函数模型;
④了解指数函数![]() 与对数函数
与对数函数![]() 互为反函数
互为反函数![]() .
.
经典例题:已知f(logax)=![]() ,其中a>0,且a≠1.
,其中a>0,且a≠1.
(1)求f(x); (2)求证:f(x)是奇函数; (3)求证:f(x)在R上为增函数.
当堂练习:
1.若![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设![]() 表示
表示![]() 的小数部分,则
的小数部分,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.0 D.
C.0 D.![]()
3.函数![]() 的值域是( )
的值域是( )
A.![]() B.[0,1]
C.[0,
B.[0,1]
C.[0,![]() D.{0}
D.{0}
4.设函数![]() 的取值范围为( )
的取值范围为( )
A.(-1,1) B.(-1,+∞) C.![]() D.
D.![]()
5.已知函数![]() ,其反函数为
,其反函数为![]() ,则
,则![]() 是( )
是( )
A.奇函数且在(0,+∞)上单调递减 B.偶函数且在(0,+∞)上单调递增
C.奇函数且在(-∞,0)上单调递减 D.偶函数且在(-∞,0)上单调递增
6.计算![]() =
.
=
.
7.若2.5x=1000,0.25y=1000,求![]() .
.
8.函数f(x)的定义域为[0,1],则函数![]() 的定义域为
.
的定义域为
.
9.已知y=loga(2-ax)在[0,1]上是x的减函数,则a的取值范围是 .
10.函数![]() 图象恒过定点
图象恒过定点![]() ,若
,若![]() 存在反函数
存在反函数![]() ,则
,则![]() 的图象必过定点 .
的图象必过定点 .
11.若集合{x,xy,lgxy}={0,x,y},则log8(x2+y2)的值为多少.
12.(1) 求函数![]() 在区间
在区间![]() 上的最值.
上的最值.
(2)已知![]() 求函数
求函数![]() 的值域.
的值域.
13.已知函数![]() 的图象关于原点对称. (1)求m的值;
的图象关于原点对称. (1)求m的值;
(2)判断f(x) 在![]() 上的单调性,并根据定义证明.
上的单调性,并根据定义证明.
14.已知函数f(x)=x2-1(x≥1)的图象是C1,函数y=g(x)的图象C2与C1关于直线y=x对称.
(1)求函数y=g(x)的解析式及定义域M;
(2)对于函数y=h(x),如果存在一个正的常数a,使得定义域A内的任意两个不等的值x1,x2都有h(x1)-h(x2)≤ax1-x2成立,则称函数y=h(x)为A的利普希茨Ⅰ类函数.试证明:y=g(x)是M上的利普希茨Ⅰ类函数.
![]() 必修1
第2章 函数概念与基本初等函数Ⅰ
必修1
第2章 函数概念与基本初等函数Ⅰ
§2.4幂函数
重难点:掌握常见幂函数的概念、图象和性质,能利用幂函数的单调性比较两个幂值的大小.
考纲要求:①了解幂函数的概念;
②结合函数![]() 的图像,了解他们的变化情况.
的图像,了解他们的变化情况.
经典例题:比较下列各组数的大小:
(1)1.5![]() ,1.7
,1.7![]() ,1; (2)(-
,1; (2)(-![]() )
)![]() ,(-
,(-![]() )
)![]() ,1.1
,1.1![]() ;
;
(3)3.8![]() ,3.9
,3.9![]() ,(-1.8)
,(-1.8)![]() ; (4)31.4,51.5.
; (4)31.4,51.5.
当堂练习:
1.函数y=(x2-2x)![]() 的定义域是( )
的定义域是( )
A.{xx≠0或x≠2} B.(-∞,0)![]() (2,+∞) C.(-∞,0)
(2,+∞) C.(-∞,0)![]() [2,+∞ ) D.(0,2)
[2,+∞ ) D.(0,2)
3.函数y=![]() 的单调递减区间为( )
的单调递减区间为( )
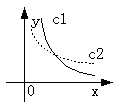 A.(-∞,1) B.(-∞,0) C.[0,+∞ ] D.(-∞,+∞)
A.(-∞,1) B.(-∞,0) C.[0,+∞ ] D.(-∞,+∞)
3.如图,曲线c1, c2分别是函数y=xm和y=xn在第一象限的图象,
那么一定有( )
A.n<m<0 B.m<n<0 C.m>n>0 D.n>m>0
4.下列命题中正确的是( )
A.当![]() 时,函数
时,函数![]() 的图象是一条直线 B.幂函数的图象都经过(0,0),(1,1)两点
的图象是一条直线 B.幂函数的图象都经过(0,0),(1,1)两点
C.幂函数的![]() 图象不可能在第四象限内 D.若幂函数
图象不可能在第四象限内 D.若幂函数![]() 为奇函数,则在定义域内是增函数
为奇函数,则在定义域内是增函数
5.下列命题正确的是( )
A. 幂函数中不存在既不是奇函数又不是偶函数的函数
B. 图象不经过(—1,1)为点的幂函数一定不是偶函数
C. 如果两个幂函数的图象具有三个公共点,那么这两个幂函数相同
D. 如果一个幂函数有反函数,那么一定是奇函数
6.用“<”或”>”连结下列各式:![]()
![]()
![]() ,
, ![]()
![]() .
.
7.函数y=![]() 在第二象限内单调递增,则m的最大负整数是_______ _.
在第二象限内单调递增,则m的最大负整数是_______ _.
8.幂函数的图象过点(2,![]() ), 则它的单调递增区间是
.
), 则它的单调递增区间是
.
9.设x∈(0, 1),幂函数y=![]() 的图象在y=x的上方,则a的取值范围是 .
的图象在y=x的上方,则a的取值范围是 .
10.函数y=![]() 在区间上
是减函数.
在区间上
是减函数.
11.试比较![]() 的大小.
的大小.
12.讨论函数y=x![]() 的定义域、值域、奇偶性、单调性。
的定义域、值域、奇偶性、单调性。
13.一个幂函数y=f (x)的图象过点(3, ![]() ),另一个幂函数y=g(x)的图象过点(-8, -2),
),另一个幂函数y=g(x)的图象过点(-8, -2),
(1)求这两个幂函数的解析式; (2)判断这两个函数的奇偶性; (3)作出这两个函数的图象,观察得f (x)< g(x)的解集.
14.已知函数y=![]() .
.
(1)求函数的定义域、值域; (2)判断函数的奇偶性; (3)求函数的单调区间.
![]() 必修1
第2章 函数概念与基本初等函数Ⅰ
必修1
第2章 函数概念与基本初等函数Ⅰ
基本初等函数Ⅰ单元测试
1.碘—131经常被用于对甲状腺的研究,它的半衰期大约是8天(即经过8天的时间,有 一半的碘—131会衰变为其他元素).今年3 月1日凌晨,在一容器中放入一定量的碘 —131,到3月25日凌晨,测得该容器内还 剩有2毫克的碘—131,则3月1日凌晨,放人该容器的碘—131的含量是( )
 A.8毫克
B.16毫克 C.32毫克
D.64毫克
A.8毫克
B.16毫克 C.32毫克
D.64毫克
2.函数y=0.5x、 y=x-2 、y=log0.3x 的图象形状
如图所示,依次大致是 ( )
A.(1)(2)(3) B.(2)(1)(3)
C.(3)(1)(2) D.(3)(2)(1)
3.下列函数中,值域为(-∞,+∞)的是( )
A.y=2x B.y=x2 C.y=x-2 D.y=log ax (a>0, a≠1)
4.下列函数中,定义域和值域都不是(-∞,+∞)的是( )
A.y=3x B.y=3x C.y=x-2 D.y=log 2x
5.若指数函数y=ax在[-1,1]上的最大值与最小值的差是1,则底数a等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.当0<a<b<1时,下列不等式中正确的是( )
A.(1-a)![]() >(1-a)b
B.(1+a)a>(1+b)b C.(1-a)b>(1-a)
>(1-a)b
B.(1+a)a>(1+b)b C.(1-a)b>(1-a)![]() D.(1-a)a>(1-b)b
D.(1-a)a>(1-b)b
7.已知函数f(x)=![]() ,则f[f(
,则f[f(![]() )]的值是( )
)]的值是( )
A.9
B.![]() C.-9 D.-
C.-9 D.-![]()
8.若0<a<1,f(x)=logax,则下列各式中成立的是( )
A.f(2)>f(![]() )>f(
)>f(![]() ) B.f(
) B.f(![]() )>f(2)>f(
)>f(2)>f(![]() ) C.f(
) C.f(![]() )>f(2)>f(
)>f(2)>f(![]() ) D.f(
) D.f(![]() )>f(
)>f(![]() )>f(2)
)>f(2)
9.在f1(x)=![]() ,f2(x)=x2,f3(x)=2x,f4(x)=log
,f2(x)=x2,f3(x)=2x,f4(x)=log![]() x四个函数中,当x1>x2>1时,使
x四个函数中,当x1>x2>1时,使![]() [f(x1)+f(x2)]<f(
[f(x1)+f(x2)]<f(![]() )成立的函数是( )
)成立的函数是( )
A.f1(x)=x![]() B.f2(x)=x2
C.f3(x)=2x D.f4(x)=log
B.f2(x)=x2
C.f3(x)=2x D.f4(x)=log![]() x
x
10.函数![]() ,给出下述命题:①
,给出下述命题:①![]() 有最小值;②当
有最小值;②当![]() 的值域为R;③当
的值域为R;③当![]() 上有反函数.则其中正确的命题是( )
上有反函数.则其中正确的命题是( )
A.①②③ B.②③ C.①② D.①③
11.不等式![]() 的解集是 .
的解集是 .
12.若函数![]() 的图象关于原点对称,则
的图象关于原点对称,则![]() .
.
13.已知0<a<b<1,设aa, ab, ba, bb中的最大值是M,最小值是m,则M= ,m= .
14.设函数![]() 的值是
.
的值是
.
15.幂函数的图象过点(2,![]() ), 则它的单调递增区间是
.
), 则它的单调递增区间是
.
16.化简与求值: (1)已知![]() ,求x的值;
,求x的值;
(2)![]() .
.
17.已知f (x)=lg(x2+1), 求满足f (100x-10x+1)-f (24)=0的x的值
18.已知![]() ,若当
,若当![]() 时,
时,![]() ,试证:
,试证: ![]()
19. 已知f (x)=![]() 且x∈[0, +∞ )
且x∈[0, +∞ )
(1) 判断f (x)的奇偶性; (2) 判断f (x)的单调性,并用定义证明;(3) 求y=f (x)的反函数的解析式.
20.已知:![]() (a>1>b>0).
(a>1>b>0).
(1)求![]() 的定义域;(2)判断
的定义域;(2)判断![]() 在其定义域内的单调性;
在其定义域内的单调性;
(3)若![]() 在(1,+∞)内恒为正,试比较a-b与1的大小.
在(1,+∞)内恒为正,试比较a-b与1的大小.
![]() 必修1
第2章 函数概念与基本初等函数Ⅰ
必修1
第2章 函数概念与基本初等函数Ⅰ
§2.5函数与方程
重难点:理解根据二次函数的图象与x轴的交点的个数判断一元二次方程的根的个数及函数零点的概念,对“在函数的零点两侧函数值乘积小于0”的理解;通过用“二分法”求方程的近似解,使学生体会函数的零点与方程根之间的关系,初步形成用函数观点处理问题的意识.
考纲要求:①结合二次函数的图像,了解函数的零点与方程根的联系,判断一元二次方程根的存在性及根的个数;
②根据具体函数的图像,能够用二分法求相应方程的近似解.
经典例题:研究方程x2-2x-3=a(a≥0)的不同实根的个数.
当堂练习:
1.如果抛物线f(x)= x2+bx+c的图象与x轴交于两点(-1,0)和(3,0),则f(x)>0的解集是( )
A. (-1,3) B.[-1,3] C.![]() D.
D. ![]()
2.已知f(x)=1-(x-a)(x-b),并且m,n是方程f(x)=0的两根,则实数a,b,m,n的大小关系可能是( )
A. m<a<b<n B.a<m<n<b C.a<m<b<n D.m<a<n<b
3.对于任意k∈[-1,1],函数f(x)=x2+(k-4)x-2k+4的值恒大于零,则x的取值范围是
A.x<0 B.x>4 C.x<1或x>3 D.x<1
4. 设方程2x+2x=10的根为![]() ,则
,则![]() ( )
( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
5.如果把函数y=f(x)在x=a及x=b之间的一段图象近似的看作直线的一段,设a≤c≤b,那么f(c)的近似值可表示为( )
A.![]() B.
B.![]() C.f(a)+
C.f(a)+![]() D.f(a)-
D.f(a)-![]()
6.关于x的一元二次方程x2+2(m+3)x+2m+14=0有两个不同的实根,且一根大于3,一根小于1,则m的取值范围是 .
7. 当a 时,关于x的一元二次方程 x2+4x+2a-12=0两个根在区间[-3,0]中.
8.若关于x的方程4x+a·2x+4=0有实数解,则实数a的取值范围是___________.
9.设x1,x2 分别是log2x=4-x 和2x+x=4的实根,则x1+x2= .
10.已知![]() ,在下列说法中:
,在下列说法中:
(1)若f(m)f(n)<0,且m<n,则方程f(x)=0在区间(m,n)内有且只有一根;
(2) 若f(m)f(n)<0,且m<n,则方程f(x)=0在区间(m,n)内至少有一根;
(3) 若f(m)f(n)>0,且m<n,则方程f(x)=0在区间(m,n)内一定没有根;
(4) 若f(m)f(n)>0,且m<n,则方程f(x)=0在区间(m,n)内至多有一根;
其中正确的命题题号是 .
11.关于x的方程mx2+2(m+3)x+2m+14=0有两个不同的实根,且一个大于4,另一个小于4,求m的取值范围.
12.已知二次函数f(x)=a(a+1)x2-(2a+1)x+1,![]() .
.
(1)求函数f(x)的图象与x轴相交所截得的弦长;
(2) 若a依次取1,2,3,4,---,n,时, 函数f(x)的图象与x轴相交所截得n条弦长分别为![]() 求
求![]() 的值.
的值.
13. 已知二次函数![]() 且满足
且满足![]()
![]() .
.
(1)证明:函数![]() 的图象交于不同的两点A,B;
的图象交于不同的两点A,B;
(2)若函数![]() 上的最小值为9,最大值为21,试求
上的最小值为9,最大值为21,试求![]() 的值;
的值;
(3)求线段AB在![]() 轴上的射影A1B1的长的取值范围.
轴上的射影A1B1的长的取值范围.
14.讨论关于x的方程lg(x-1)+lg(3-x)=lg(a-x)的实根个数.
![]() 必修1
第2章 函数概念与基本初等函数Ⅰ
必修1
第2章 函数概念与基本初等函数Ⅰ
§2.6函数模型及其应用
重难点:将实际问题转化为函数模型,比较常数函数、一次函数、指数函数、对数函数模型的增长差异,结合实例体会直线上升、指数爆炸、对数增长等不同类型的函数增长的含义.
考纲要求:①了解指数函数、对数函数以及幂函数的增长特征,知道直线上升、指数增长、对数增长等不同函数类型增长的含义;
②了解函数模型(如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型)的广泛应用.
经典例题:1995年我国人口总数是12亿.如果人口的自然年增长率控制在1.25%,问哪一年我国人口总数将超过14亿.
当堂练习:
1.某物体一天中的温度T是时间t的函数: T(t)=t3-3t+60,时间单位是小时,温度单位是![]() ,当t=0表示中午12:00,其后t值取为正,则上午8时的温度是( )
,当t=0表示中午12:00,其后t值取为正,则上午8时的温度是( )
A.8 ![]() B.112
B.112![]() C.58
C.58 ![]() D.18
D.18![]()
2.某商店卖A、B两种价格不同的商品,由于商品A连续两次提价20%,同时商品B连续两次降价20%,结果都以每件23.04元售出,若商店同时售出这两种商品各一件,则与价格不升、不降的情况相比较,商店盈利的情况是:( )
A.多赚5.92元 B.少赚5.92元 C.多赚28.92元 D.盈利相同
3.某厂生产中所需一些配件可以外购,也可以自己生产,如外购,每个价格是1.10元;如果自己生产,则每月的固定成本将增加800元,并且生产每个配件的材料和劳力需0.60元,则决定此配件外购或自产的转折点是( )件(即生产多少件以上自产合算)
A.1000 B.1200 C.1400 D.1600
4.在一次数学实验中, 运用图形计算器采集到如下一组数据.
| x | -2.0 | -1.0 | 0 | 1.00 | 2.00 | 3.00 |
| y | 0.24 | 0.51 | 1 | 2.02 | 3.98 | 8.02 |
则x,y的函数关系与下列哪类函数最接近?(其中a,b为待定系数) ( )
A.y=a+bX B.y=a+bx C.y=a+logbx D.y=a+b/x
5.某产品的总成本y(万元)与产量x(台)之间的函数关系式是y=3000+20x-0.1x2(0<x<240,x∈N),若每台产品的售价为25万元,则生产者不亏本时(销售收入不小于总成本)的最低产量是( )
A.100台 B.120台 C.150台 D.180台
6.购买手机的“全球通”卡,使用须付“基本月租费”(每月需交的固定费用)50元,在市内通话时每分钟另收话费0.40元;购买“神州行”卡,使用时不收“基本月租费”,但在市内通话时每分钟话费为0.60元.若某用户每月手机费预算为120元,则它购买_________卡才合算.
7.某商场购进一批单价为6元的日用品,销售一段时间后,为了获得更多利润,商场决定提高销售价格。经试验发现,若按每件20元的价格销售时,每月能卖360件,若按25元的价格销售时,每月能卖210件,假定每月销售件数y (件)是价格x (元/件)的一次函数。试求y与x之间的关系式 .
在商品不积压,且不考虑其它因素的条件下,问销售价格定为 时,才能时每月获得最大利润.
每月的最大利润是 .
8.某企业生产的新产品必须先靠广告来打开销路.该产品的广告效应应该是产品的销售额与广告费之间的差.如果销售额与广告费的算术平方根成正比,根据对市场进行抽样调查显示:每付出100元的广告费,所得的销售额是1000元.问该企业应该投入 广告费,才能获得最大的广告效应.
9.商店出售茶壶和茶杯,茶壶每只定价为20元,茶杯每只定价5元,该店制定了两种优惠办法:(1)买一只茶壶送一只茶杯;(2)按总价的92%付款;某顾客需购茶壶4只,茶杯若干只(不少于4只).则当购买茶杯数 时, 按(2)方法更省钱.
10.一块形状为直角三角形的铁皮,直角边长分别为40cm和60cm,现要将它剪成一个矩形,并以此三角形的直角为矩形的一个角,则矩形的最大面积是 .
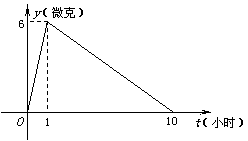 11.某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y与时间t之间近似满足如图所示的曲线.
11.某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y与时间t之间近似满足如图所示的曲线.
(1)写出服药后y与t之间的函数关系式;
(2)据测定:每毫升血液中含药量不少于4微克时治疗疾病有效,假若某病人一天中第一次服药时间为上午7:00,问一天中怎样安排服药的时间(共4次)效果最佳.
12.某省两个相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为公共交通车,已知如果该列火车每次拖4节车厢,能来回16次;如果每次拖7节车厢,则能来回10次.每日来回次数是每次拖挂车厢个数的一次函数,每节车厢一次能载客110人,问:这列火车每天来回多少次,每次应拖挂多少节车厢才能使营运人数最多?并求出每天最多的营运人数.
13.市场营销人员对过去几年某商品的价格及销售数量的关系作数据分析,发现有如下规律:该商品的价格每上涨 x%(x>0),销售数量就减少kx% (其中k为正常数).目前,该商品定价为a元, 统计其销售数量为b个.
(1)当k=![]() 时,该商品的价格上涨多少,就能使销售的总金额达到最大.
时,该商品的价格上涨多少,就能使销售的总金额达到最大.
(2)在适当的涨价过程中,求使销售总金额不断增加时k的取值范围.
14.某工厂今年1月、2月、3月生产某种产品的数量分别为l万件,1.2万件,1.3万件.为了估测以后每个月的产量,以这三个月的产品数量为依据.用一个函数模拟该产品的月产量y与月份x的关系,模拟函数可以选用二次函数或函数![]() (其中a,b,c为常数).已知4月份该产品的产量为1.37万件,请问用以上哪个函数作为模拟函数较好.并说明理由.
(其中a,b,c为常数).已知4月份该产品的产量为1.37万件,请问用以上哪个函数作为模拟函数较好.并说明理由.
![]() 必修1
第2章 函数概念与基本初等函数Ⅰ
必修1
第2章 函数概念与基本初等函数Ⅰ
函数的概念与基本初等函数Ⅰ章节测试
1.函数![]() 的定义域是( )
的定义域是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.log5(![]() +1)+log2(
+1)+log2(![]() -1)=a,则log5(
-1)=a,则log5(![]() -1)+log2(
-1)+log2(![]() +1)= ( )
+1)= ( )
A.-a
B.![]() C.a-1
D.1-a
C.a-1
D.1-a
3.关于x的方程![]()
![]() 有实根则a的取值范围是( )
有实根则a的取值范围是( )
A. a![]() B.
B. ![]() C.
C.![]() D. a<0
D. a<0
4.已知集合![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.函数f(x)的图象与g(x)=(![]() )x的图象关于直线y=x对称,则f(2x-x2)的单调增区间是( )
)x的图象关于直线y=x对称,则f(2x-x2)的单调增区间是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.二次函数y=f(x)满足f(3+x)=f(3-x),且f(x)=0有两个实根x1、x2,则x1+x2等于( )
A.0 B.3 C.6 D.不能确定
7.下面四个结论:①偶函数的图象一定与y轴相交;②奇函数的图象一定过原点;③偶函数的图象关于y轴对称;④既是奇函数又是偶函数的函数一定是f(x)=0(x∈R),其中真命题的个数是( )
A.1 B.2 C.3 D.4
8.设![]() 的值为( )
的值为( )
A.1
B.-1 C.-![]() D.
D.![]()
9.设函数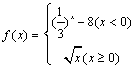 ,若f(a)>1,则实数a的取值范围是( )
,若f(a)>1,则实数a的取值范围是( )
A.![]() B.
B.![]() ∪
∪![]() C.(1,+∞) D.
C.(1,+∞) D.![]() ∪(0,+∞)
∪(0,+∞)
10.R上的函数y=f(x)不恒为零,同时满足f(x+y)=f(x)f(y),且当x>0时,f(x)>1,则当x<0时,一定有( )
A.f(x)<-1 B.-1<f(x)<0 C.f(x)>1 D.0<f(x)<1
11.已知函数![]() 的定义域是[2,3],若
的定义域是[2,3],若![]() ,则函数
,则函数![]() 的定义域是 .
的定义域是 .
12.已知函数![]() ,则
,则![]() 的值是 .
的值是 .
13.设函数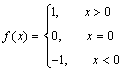 ,则方程
,则方程![]() 的解为
.
的解为
.
14.密码的使用对现代社会是极其重要的.有一种密码其明文和密文的字母按A、B、C…与26个自然数1,2,3,…依次对应。设明文的字母对应的自然数为![]() ,译为密文的字母对应的自然数为
,译为密文的字母对应的自然数为![]() .例如,有一种译码方法是按照以下的对应法则实现的:
.例如,有一种译码方法是按照以下的对应法则实现的:![]() ,其中
,其中![]() 是
是![]() 被26除所得的余数与1之和(
被26除所得的余数与1之和(![]() ).按照此对应法则,明文A译为了密文F,那么密文UI译成明文为______________.
).按照此对应法则,明文A译为了密文F,那么密文UI译成明文为______________.
15.设函数 若
若![]() ,则x0的取值范围是
.
,则x0的取值范围是
.
16.设xÎ[2,4],函数![]() 的最大值为0,最小值为
的最大值为0,最小值为![]() ,求a的值.
,求a的值.
17.设![]() 的定义域是区间[0,1],
的定义域是区间[0,1],
(1)求g(x)的解析式; (2)求g(x)的单调区间; (3)求g(x)的值域.
18.已知f(x)=![]() ,(x
,(x![]() 2).
2).
(1)求f —1(x)及其单调区间;(2)若g(x)=3+![]() +
+![]() ,求其最小值.
,求其最小值.
19.在中国轻纺市场,当季节即将来临时,季节性服装价格呈上升趋势,设某服装开始时定价为10元,并且每周(七天)涨价2元,5周后保持20元的价格平稳销售,10周后当季节即将过去时,平均每周削价2元,直到16周末,该服装已不再销售.
(1)试建立价格P与周次t的函数关系.
(2)若此服装每件进价Q与周次t之间的关系为Q=-0.125(t-8)2+12,t∈[0,16],t∈N.试问:该服装第几周每件销售利润L最大.
20.巳知函数f(x)=loga![]() ,定义域为[α,β],值域为[logaa(β—1),logaa(α—1)],且f(x)在 [α,β]上是减函数.
,定义域为[α,β],值域为[logaa(β—1),logaa(α—1)],且f(x)在 [α,β]上是减函数.
(1)求证:α>2; (2)求实数a的取值范围.
![]() 必修1
必修1综合测试
必修1
必修1综合测试
1.设全集U=R,集合![]() ,
,![]() ,则
,则![]() 为( )
为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.方程![]() 5
5![]() =
=![]() 5
5![]() 的解集是( )
的解集是( )
A.{3} B.{-1} C.{-1,3} D.{1,3}
3.函数![]() 的定义域是( )
的定义域是( )
A.![]() B.
B.![]() C.
C.![]()
![]() D.
D.![]()
![]()
4.下表表示y是x的函数,则函数的值域是( )
|
|
|
|
|
|
|
| 2 | 3 | 4 | 5 |
A.![]() B.
B.![]() C.
C.![]() D.N
D.N
5.已知![]() ,
,![]() ,
,![]() ,则
,则![]() 之间的大小关系为( )
之间的大小关系为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知函数![]() 若
若![]() ,则x的值为( )
,则x的值为( )
A.2 B.3 C.2或3 D.-2或3
7.函数![]() 的图像( )
的图像( )
A.关于x轴对称 B.关于y轴对称 C.关于原点对称 D.关于直线![]() 对称
对称
8.根据表格中的数据,可以判定方程ex-x-2=0的一个根所在的区间为( )
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
A.(-1,0) B.(0,1) C. (1,2) D. (2,3)
9若![]() ,则f(5)的值等于( )
,则f(5)的值等于( )
A.10 B.11 C.12 D.13
10.已知函数f(x)满足![]() ,则f(x)的解析式是( )
,则f(x)的解析式是( )
A.log2x B.-log2x C.2-x D.x-2
11.已知A={(x,y)x+y-2=0},B={(x,y)x-2y+4=0},C={(x,y)y=3x+b},若(A∩B)⊆C,则b= .
12.已知函数![]() 是偶函数,且在(0,+∞)是减函数,则整数
是偶函数,且在(0,+∞)是减函数,则整数![]() 的值是
.
的值是
.
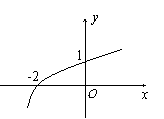 13.已知函数
13.已知函数![]() 的图象如图所示,则a、b的值分别为
、
.
的图象如图所示,则a、b的值分别为
、
.
14.已知定义在实数集R上的偶函数![]() 在区间
在区间![]() 上是单调增函数
上是单调增函数
,若f(1)<f(2x-1),则x的取值范围是 .
15.已知函数![]() ,令
,令![]()
(即f(x)和g(x)中的较大者),则![]() 的最小值是___________.
的最小值是___________.
16.设![]() ,求函数
,求函数![]() 的最大值和最小值.
的最大值和最小值.
17.已知关于x的二次函数![]() .
.
(1)求证:对于任意![]() ,方程
,方程![]() 必有实数根;
必有实数根;
(2)若![]() ,求证:方程
,求证:方程![]() 在区间
在区间![]() 上各有一个实数根.
上各有一个实数根.
18.对于函数![]() ,
,
(1)判断并证明函数的单调性; (2)是否存在实数a,使函数![]() 为奇函数.证明你的结论.
为奇函数.证明你的结论.
19. 在距A城50km的B地发现稀有金属矿藏,现知由A至某方向有一条直铁路AX,B到该铁路的距离为30km,为在AB之间运送物资,拟在铁路AX上的某点C处筑一直公路通到B地.已知单位重量货物的铁路运费与运输距离成正比,比例系数为![]() (
(![]() >0); 单位重量货物的公路运费与运输距离的平方成正比,比例系数为
>0); 单位重量货物的公路运费与运输距离的平方成正比,比例系数为![]() (
(![]() >0).设单位重量货物的总运费为y元,AC之间的距离为xkm.
>0).设单位重量货物的总运费为y元,AC之间的距离为xkm.
(1) 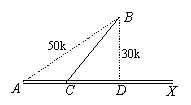 将y表示成x的函数;(2)若
将y表示成x的函数;(2)若![]() ,则当x为何值时,单位重量货物的总运费最少.并求出最少运费.
,则当x为何值时,单位重量货物的总运费最少.并求出最少运费.
20.已知定理:“若![]() 为常数,
为常数,![]() 满足
满足![]() ,则函数
,则函数![]() 的图象关于点
的图象关于点![]() 中心对称”.设函数
中心对称”.设函数![]() ,定义域为A.
,定义域为A.
⑴试证明![]() 的图象关于点
的图象关于点![]() 成中心对称;
成中心对称;
⑵当![]() 时,求证:
时,求证:![]() ;(3)对于给定的
;(3)对于给定的![]() ,设计构造过程:
,设计构造过程:![]()
![]() ,…,
,…,![]() .如果
.如果![]() ,构造过程将继续下去;如果
,构造过程将继续下去;如果![]() ,构造过程将停止.若对任意
,构造过程将停止.若对任意![]() ,构造过程可以无限进行下去,求a的值.
,构造过程可以无限进行下去,求a的值.
必修1参考答案
第1章 集 合
§1.1 集合的含义及其表示
经典例题:解:由集合中元素的互异性知
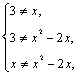 解之得x≠-1,且x≠0,且x≠3.
解之得x≠-1,且x≠0,且x≠3.
当堂练习:
1.
D; 2. B; 3. A;4. C;5. B;6.![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ; 7. {
; 7. {![]() };
};
8.
{(0,8),(1,7),(2,4)};9. ![]() ;10. 2或4;
;10. 2或4;
11.因为数集中的元素是互异的,所有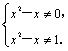 ∵x2-x=0的解是x=0或x=1, ∴x2-x≠0的解是x≠0或x≠1; ∵x2-x=1的解是x=
∵x2-x=0的解是x=0或x=1, ∴x2-x≠0的解是x≠0或x≠1; ∵x2-x=1的解是x=![]() 或x=
或x=![]() , ∴x2-x≠1的解为x≠
, ∴x2-x≠1的解为x≠![]() 且x≠
且x≠![]() ; 因此,x不能取的数值是0,1,
; 因此,x不能取的数值是0,1,![]() .
.
12.∵![]()
![]() N(x
N(x![]() N), ∴6-x=1,2,3,4,6(x
N), ∴6-x=1,2,3,4,6(x![]() N),即x=5,4,3,2,0.故A={0,2,3,4,5}. 13.(1)当a=0时,方程2x+1=0只有一根
N),即x=5,4,3,2,0.故A={0,2,3,4,5}. 13.(1)当a=0时,方程2x+1=0只有一根![]() ;当a≠0时,△=0,即4-4a=0,所以a=1,这时
;当a≠0时,△=0,即4-4a=0,所以a=1,这时![]() .所以,当a=0或a=1时,A中只有一个元素分别为
.所以,当a=0或a=1时,A中只有一个元素分别为![]() 或-1.(2)A中至多有一元素包括两种情形即A中有一个元素和A是空集.当A是空集时,则有
或-1.(2)A中至多有一元素包括两种情形即A中有一个元素和A是空集.当A是空集时,则有![]() ,解得a>1;结合(1)知,当a=0或a≥1时,A中至多有一个元素. 14.(1)
,解得a>1;结合(1)知,当a=0或a≥1时,A中至多有一个元素. 14.(1)![]() ; (2)集合A非空,故存在a
; (2)集合A非空,故存在a![]() A, a
A, a![]() 1,
1,![]()
![]() 且
且![]() ,即
,即![]() 时,有
时,有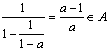 ,且
,且![]() ,
,![]()
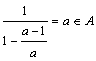 ,
,![]() 三个数为
三个数为![]() ,再证这三数两两互不相等即可.
,再证这三数两两互不相等即可.
§1.2 子集、全集、补集
经典例题:解:(1)2=8×2+14×(-1),且2∈Z,-1∈Z,
2=8×(-5)+14×3,且-5∈Z,3∈Z等.所以2∈A.
(2)任取x0∈B,则x0=2k,k∈Z.∵2k=8×(-5k)+14×3k,且-5k∈Z,3k∈Z,∴2k∈A,即B ![]() A.
A.
任取y0∈A,则y0=8m+14n,m、n∈Z,∴y0=8m+14n=2(4m+7n),且4m+7n∈Z.∴8m+14n∈B,即A![]() B.
B.
由B ![]() A且A
A且A![]() B,∴A=B.
B,∴A=B.
当堂练习:
1. B ; 2. A ; 3. A ;4. D ;5. D ;6. ![]() ,{0},{2},{0,2};7. M
,{0},{2},{0,2};7. M![]() P;8. 7. 9. {
P;8. 7. 9. {![]() };10. m=0 或
};10. m=0 或![]() 或-
或-![]() ;
;
![]()
![]() 11. (1)A
11. (1)A![]() B
B![]() C.(2)
C.(2)![]() ,
,![]() C
C![]() A
A![]() B.
B.
(3)![]() ,
, ![]() A
A![]() B=C.
B=C.
(4)![]()
![]() 当
当![]() 时,2k+1是奇数,k+2是整数,
时,2k+1是奇数,k+2是整数,
![]() A
A![]() B.
B.
12.
(1)当![]() 时,
时,![]() ,符合条件
,符合条件
由![]()
(2)![]()
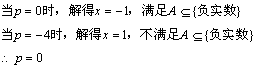
(3)当![]() 时,要
时,要![]() 则
则
 综上所述,
综上所述,![]() .
.
13.显然![]() ,若x=1,则z=2x=2,
从而2 y=8, y=4,得A={8,1,2,4},
,若x=1,则z=2x=2,
从而2 y=8, y=4,得A={8,1,2,4},![]() u A={6, 12};若y=1,则2x=8, x=4, 从而z=2,
得A={8,1,2,4},
u A={6, 12};若y=1,则2x=8, x=4, 从而z=2,
得A={8,1,2,4},![]() u A={6, 12};若z=1, 则xy=8, x=2x,不可能.综上所述,
u A={6, 12};若z=1, 则xy=8, x=2x,不可能.综上所述, ![]() u A={6, 12}.
u A={6, 12}.
14.(1)∵![]() u A=U,∴A=
u A=U,∴A=![]() ,那么方程x2-5qx+4=0的根x≠1,2,3,4,5或无解.
,那么方程x2-5qx+4=0的根x≠1,2,3,4,5或无解.
x≠1时,q≠1,x≠2,q≠![]() ;x≠3,4,5时,q≠
;x≠3,4,5时,q≠![]() ,1,
,1,![]() .若△<0,即-
.若△<0,即-![]() <q<
<q<![]() 时,方程无实根,当然A中方程在全集U中无实根.综上,q的取值范围是{q-
时,方程无实根,当然A中方程在全集U中无实根.综上,q的取值范围是{q-![]() <q<
<q<![]() 或q≠1,
或q≠1,![]() ,
,![]() ,
,![]()
![]() .(2)因为
.(2)因为![]() u A中有四个元素,所有A为单元集合,由上一问知q=
u A中有四个元素,所有A为单元集合,由上一问知q=![]() 时,A={2},
时,A={2},![]() u A={1,3,4,5};q=
u A={1,3,4,5};q=![]() 时,A={3},
时,A={3},![]() u A={1,2,4,5};q=
u A={1,2,4,5};q=![]() 时,A={5},
时,A={5},![]() u A={1,2,3,4}.(3)因为A为双元素集合,由(1)知q=1时,A={1,4},
u A={1,2,3,4}.(3)因为A为双元素集合,由(1)知q=1时,A={1,4},![]() u A={2,3,5}.
u A={2,3,5}.
§1.3 交集、并集
经典例题:解: A= ![]() ,∵A
,∵A![]() B=B, ∴B
B=B, ∴B![]() A.
A.
若B= ![]() ,则
,则![]() ;若B=
;若B=![]() ,则0
,则0![]() -0+4=0,a
-0+4=0,a![]()
![]() ;若B=
;若B=![]() 则a·1
则a·1![]() -2·1+4=0,a=-2,-2
-2·1+4=0,a=-2,-2![]() ,
,![]() 不合;若B=
不合;若B=![]()
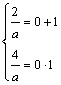 ,
,![]() . ∴
. ∴![]() .
.
当堂练习:
1.
B ; 2. C ; 3. B ;4.
B ;5. D ;6.[-1,+∞];7.{y|-3≤y≤3};8.![]()
9.![]() ; 10.{(1,2)};
; 10.{(1,2)};
11.
∵![]() , ∴
, ∴![]() 若
若 ![]() 这时
这时![]() 若
若![]()
这时![]() 不符合集合中元素的互异性.若
不符合集合中元素的互异性.若![]()
这时M=![]() ∴
∴![]()
12.∵![]() ∴
∴![]() ∴
∴![]() ∴
∴![]()
∵![]() ∴
∴![]() 又 ∵
又 ∵![]() ∴
∴![]()
∴![]() ∴
∴![]() .
.
13. 利用韦恩图求解得U={1,2,3,4,5,6,7,8,9},从而![]() u(A∪B)=
{2,7,9}, A={1,3,5},B={3,4,6,8}.
u(A∪B)=
{2,7,9}, A={1,3,5},B={3,4,6,8}.
14. (1)当B=A时,可得a=1;(2)当B={0}时,得a=-1; (3)当B={-4}时,不合题意; (4)当B=![]() 时,由
时,由![]() 得
得![]() ,综上所述,
,综上所述, ![]() 或a=1.
或a=1.
§1.4 单元测试
1.D; 2.B; 3.D; 4.B; 5.C; 6.D; 7.B ; 8.B ; 9.B; 10.B; 11.B; 12.C;
13.0或2; 14.7; 15.{2,5,10}; 16. 9;
17.由韦恩图易得:A={1,2,8,9} B={3,6,7,9} A∪B={1,2,3,6,7,8,9}
18.由条件得B=![]() ,从而CUB=
,从而CUB=![]() , A∪B=
, A∪B=![]() ,
,
A∩B=![]() ,A∩(CUB)=
,A∩(CUB)= ![]() , (CU A) ∩(CUB)=
, (CU A) ∩(CUB)=
![]()
19.∵A∩B={![]() },∴
},∴![]() ∈A,代入得p=-
∈A,代入得p=-![]() ∴A={
∴A={![]() ,2}
,2}
又∵A∩B={![]() },∴
},∴![]() ∈B,代入得q=-1 ∴B={
∈B,代入得q=-1 ∴B={![]() ,-1}
,-1}
则A∪B={-1,![]() ,2}
,2}
20.
(1)由方程组![]() 得
得![]() ,由
,由![]() 得
得![]() ;
;
(2)由(1)可知![]() .
.
21.由条件得a1= a12,从而a1=1, a4=9, 若 a22= a4=9,则a2=3,所以a3+ a32=124-10-3-81=30,
a3=5,符合题意; 若a32== a4=9,则a3=3,得a2=2,这与"A∪B的所有元素之和为124"这一条件矛盾,所以A={1,3,5,9},B={1,9,25,81}.
22.A={xx2-3x+2=0}={1,2} 由x2-ax+3a-5=0,知Δ=a2-4(3a-5)=a2-12a+20=(a-2)(a-10)
(1)当2<a<10时,Δ<0,B=φ![]() A
A
(2)当a≤2或a≥10时,Δ≥0,则B≠φ
若x=1,由1-a+3a-5=0得a=2此时B={xx2-2x+1=0}={1}![]() A;
A;
若x=2,由4-2a+3a-5=0,得a=1此时B={2,-1}![]() A.
A.
综上所述,当2≤a<10时,均有A∩B=B
第2章 函数概念与基本初等函数Ⅰ
§2.1.1 函数的概念和图象
经典例题:
解:(1)∵f(x)的定义域为[0,1], ∴f(x2+1)的定义域满足0≤x2+1≤1. ∴-1≤x2≤0.
∴x=0. ∴函数的定义域为{0}.
(2)由题意,得![]() 得
得![]()
则①当1-m<m,即m>![]() 时,无解; ②当1-m=m,即m=
时,无解; ②当1-m=m,即m=![]() 时,x=m=
时,x=m=![]() ;
;
③当1-m>m>0,即0<m<![]() 时,m≤x≤1-m.
时,m≤x≤1-m.
综上所述,当0<m≤![]() 时,G(x)的定义域为{xm≤x≤1-m}.
时,G(x)的定义域为{xm≤x≤1-m}.
当堂练习:
1.
A ; 2. C ; 3. C ;4.
D ;5. D ; 6. 5, ![]() ;7.
;7. ![]() ;8.
;8. ![]() ;9. f(x)= -6x2+12x+9; 10.
;9. f(x)= -6x2+12x+9; 10.![]() ;
;
11.(1)
![]() ,(2)由
,(2)由![]() 得(-
得(-![]() ,-1)
,-1)![]() (-1,0).12. 设
(-1,0).12. 设![]() ,则
,则![]() ,当
,当![]() 时,y有最小值
时,y有最小值![]() ,所求函数的值域为
,所求函数的值域为![]() .
.
13. 解:因抛物线的对称轴是x= -2,所以分类讨论:
(1)
①当t+1<-2,即t<-3时,
g(t)=f(t+1);②当![]() ,即
,即![]() 时g(t)=f(-2);③当t>-2时, g(t)=f(t).
时g(t)=f(-2);③当t>-2时, g(t)=f(t).
(2)
①当 -2-t![]() (t+1)-(-2), 即t
(t+1)-(-2), 即t![]() 时, h(t)= f(t); ②当-2-t< (t+1)-(-2), 即t
时, h(t)= f(t); ②当-2-t< (t+1)-(-2), 即t![]() 时, h(t)= f(t+1).
时, h(t)= f(t+1).
综上所述: ,
,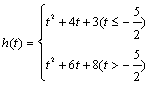
14. 解:(1)当![]() 时,S=x;当
时,S=x;当![]() 时,S=2;当
时,S=2;当![]() 时,S=6-x。 定义域是(0,6),值域是(0,2) (2) f[f(3)]=f(2)=2.
时,S=6-x。 定义域是(0,6),值域是(0,2) (2) f[f(3)]=f(2)=2.
§2.1.2 函数的简单性质
经典例题:
解析:本题可采用三种解法.
方法一:直接根据奇、偶函数的定义.
由f(x)是奇函数得f(-a)=-f(a),f(-b)=-f(b),g(a)=f(a),g(b)=f(b),g(-a)=g(a),g(-b)=g(b).
∴以上四个不等式分别可简化为①f(b)>0;②f(b)<0;③f(a)>0;④f(a)<0.
又∵f(x)是奇函数又是增函数,且a>b>0,故f(a)>f(b)>f(0)=0,从而以上不等式中①、③成立.故选C.
方法二:结合函数图象.
由下图,分析得f(a)=g(a)=g(-a)=-f(-a),f(b)=g(b)=g(-b)=-f(-b).
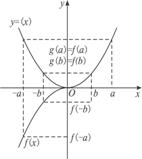
从而根据所给结论,得到①与③是正确的.故选C.
方法三:利用间接法,即构造满足题意的两个函数模型f(x)=x,g(x)=x,取特殊值a、b.如a=2,b=1.可验证正确的是①与③,故选C.
答案:C
当堂练习:
1. B ;
2. D ; 3. B ;4. D
;5. A ; 6. 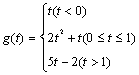 ;7.
;7. ![]() ;
;
8. ![]() >
>![]() ;9. x=-1; 10. (
;9. x=-1; 10. (![]() );
);
11.
解: (1)函数![]() ,设
,设![]() 时,
时,![]()
![]()
![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递增;
上单调递增;
(2)从而当x=1时,![]() 有最小值
有最小值![]() .
.
12. 解:(1)任取![]() ,
,![]() ,且
,且![]() ,
,![]() , 因为
, 因为![]() ,
,
![]() ,
,![]() ,所以
,所以![]() ,即
,即![]() ,故
,故![]() 在
在![]() 上单调递增.
上单调递增.
(2)因为![]() 在
在![]() 上单调递增,
上单调递增,![]() 的定义域、值域都是
的定义域、值域都是![]()
![]() ,
,
即![]() 是方程
是方程![]() 的两个不等的正根
的两个不等的正根![]() 有两个不等的正根.
有两个不等的正根.
所以![]() ,
,![]()
![]()
∴![]() ,
,
∴![]() 时,
时,![]() 取最大值
取最大值![]() .
.
13.解: (1)利用定义易证之; (2)由(1)得![]() =
=![]() .
.
14. 解: (1)![]() ; (2)当
; (2)当![]() 时, f1(x)单调递减, 当
时, f1(x)单调递减, 当![]() 时, f1(x)单调递增; 当
时, f1(x)单调递增; 当![]() 时, f2(z) 单调递减, 当
时, f2(z) 单调递减, 当![]() 时, f1(x)单调递增.
时, f1(x)单调递增.
(3)
当![]() 和
和![]() 时, f(x)分别单调递减;
时, f(x)分别单调递减;
当![]() 和
和![]() 分别单调递增.
分别单调递增.
§2.1.3单元测试
1.C; 2. A; 3.C; 4.C; 5.B; 6.C; 7.B; 8.D; 9.B; 10.D; 11.D; 12.B;
13. 2.5; 14. g(x)=2x-3; 15. 1或2; 16. x6-6x4+9x2-2;
17.解: (1)在![]() 和
和![]() 上分别单调递减; 在[-1,1]和
上分别单调递减; 在[-1,1]和![]() 上分别单调递增.
上分别单调递增.
(2) 值域是[0,4]
18.(1)证明:对任意x1、x2∈R,∵a>0,∴f(x1)+f(x2)-2f(![]() )
)
=ax12+x1+ax22+x2-2[a(![]() )2+
)2+![]() ]
]
=![]() a(x1-x2)2≥0.∴f(
a(x1-x2)2≥0.∴f(![]() )≤
)≤![]() [f(x1)+f(x2)],∴f(x)是凹函数.
[f(x1)+f(x2)],∴f(x)是凹函数.
19.(1)证明:令x=y=0,则f(0)+f(0)=f(0),故f(0)=0.
令y=-x,则f(x)+f(-x)=f(![]() )=f(0)=0.∴f(-x)=-f(x),即函数f(x)是奇函数.
)=f(0)=0.∴f(-x)=-f(x),即函数f(x)是奇函数.
(2)证明:设x1<x2∈(-1,1),则f(x1)-f(x2)=f(x1)+f(-x2)=f(![]() ).
).
∵x1<x2∈(-1,1),∴x2-x1>0,-1<x1x2<1.因此![]() <0,∴f(
<0,∴f(![]() )>0,
)>0,
即f(x1)>f(x2).∴函数f(x)在(-1,1)上是减函数.
20.解:(1)设P(x1,y1),Q(x2,y2)(x1≠x2)是函数f(x)=![]() 的图象上的两个“稳定点”,
的图象上的两个“稳定点”,
∴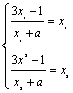 ,即有x12+ax1=3x1-1(x1≠-a),x22+ax2=3x2-1(x2≠-a).
,即有x12+ax1=3x1-1(x1≠-a),x22+ax2=3x2-1(x2≠-a).
有x12+(a-3)x1+1=0(x1≠-a),x22+(a-3)x2+1=0(x2≠-a).
∴x1、x2是方程x2+(a-3)x+1=0两根,且∵x1, x2≠-a,∴x≠-a,
∴方程x2+(a-3)x+1=0有两个相异的实根且不等于-a.
∴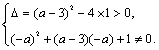 ∴a>5或a<1且a≠-
∴a>5或a<1且a≠-![]() .
.
∴a的范围是(-∞,-![]() )∪(-
)∪(-![]() ,1)∪(5,+∞).
(2)∵f(x)是R上的奇函数,
,1)∪(5,+∞).
(2)∵f(x)是R上的奇函数,
∴f(-0)=-f(0),即f(0)=0.∴原点(0,0)是函数f(x)的“稳定点”,若f(x)还有稳定点(x0,y0),则∵f(x)为奇函数,f(-x0)=-f(x0),f(x0)=x0,∴f(-x0)=-x0,这说明:(-x0,-x0)也是f(x)的“稳定点”.综上所述可知,f(x)图象上的“稳定点”除原点外是成对出现的,而且原点也是其“稳定点”,
∴它的个数为奇数.
§2.2指数函数
经典例题:
解:由题意可知,函数y=3![]() 的定义域为实数R.设u=-x2+2x+3(x∈R),则f(u)=3u,
的定义域为实数R.设u=-x2+2x+3(x∈R),则f(u)=3u,
故原函数由u=-x2+2x+3与f(u)=3u复合而成.∵f(u)=3u在R上是增函数,而u=-x2+2x+3
=-(x-1)2+4在x∈(-∞,1)上是增函数,在[1,+∞]上是减函数.
∴y=f(x)在x∈(-∞,1)上是增函数,在[1,+∞]上是减函数.
又知u≤4,此时x=1,∴当x=1时,ymax=f(1)=81,而3![]() >0,
>0,
∴函数y=f(x)的值域为(0,81)
当堂练习:
1.A
; 2. C ; 3. B ;4. A
;5. A ; 6. ![]() ;7.
;7. ![]() ;8.
;8. ![]() ;9. (1,0);10.
;9. (1,0);10. ![]() ;
;
11.(1)
原式=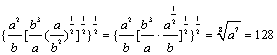
(2)原式=![]()
![]()
12. (1)解:f(x)=![]() , ∵x
, ∵x![]() [-3,2], ∴
[-3,2], ∴![]() .则当2-x=
.则当2-x=![]() ,即x=1时,f(x)有最小值
,即x=1时,f(x)有最小值![]() ;当2-x=8,即x=-3时,f(x)有最大值57.
;当2-x=8,即x=-3时,f(x)有最大值57.
(2)解:设![]() ,当
,当![]() [0,2]时,
[0,2]时,![]() ,
,
当0<a<1时,![]() ,矛盾;当a>1时,
,矛盾;当a>1时,![]() .综上所述,a=2.
.综上所述,a=2.
(3)原函数化为![]() ,当a>1时,因
,当a>1时,因![]() ,得
,得![]() ,从而
,从而![]() ,同理, 当0<a<1时,
,同理, 当0<a<1时,![]() .
.
13. (1)由![]() 得
得![]() 时
时![]() 单调递增,而
单调递增,而![]() 是单调减函数,所以原函数的递减区间是
是单调减函数,所以原函数的递减区间是![]() ,递增区间是
,递增区间是![]() ; 值域是
; 值域是![]() .
(2)
.
(2)![]()
![]() ,所以值域是
,所以值域是![]() ;单调减区间是
;单调减区间是![]() ,单调增区间
,单调增区间![]() .
(3).设
.
(3).设![]() 的定义域是
的定义域是![]() ,当
,当![]() 时,
时,![]() 单调递增,又
单调递增,又![]() 是单调增函数,所以原函数的递增区间是
是单调增函数,所以原函数的递增区间是![]() .
.
14.解: (1)任取![]() 且
且![]() ,则
,则![]() ,又
,又![]() =
=![]() ,
,![]()
![]() ,故f(x)在
,故f(x)在![]() 上为增函数.
上为增函数.
(2)设存在![]() ,满足
,满足![]() ,则
,则![]() ,由
,由![]() 得
得![]() ,即
,即![]() 与假设矛盾,所以方程无负数解.
与假设矛盾,所以方程无负数解.
§2.3对数函数
经典例题:(1)解:设t=logax,则t∈R,∴x=at(x>0).则f(t)=![]() =
=![]() (at-a-t).
(at-a-t).
(2)证明:∵f(-x)=![]() (a-x-ax)=-
(a-x-ax)=-![]() (ax-a-x)=-f(x),∴f(x)为奇函数.
(ax-a-x)=-f(x),∴f(x)为奇函数.
(3)证明:设x1、x2∈R,且x1<x2,则f(x2)-f(x1)=![]() [(a
[(a![]() -a-
-a-![]() )-(a
)-(a![]() -a-
-a-![]() )]
)]
=![]() ;(a
;(a![]() -a
-a![]() )+a-
)+a-![]() a-
a-![]() (a
(a![]() -a
-a![]() )]=
)]=![]() (a
(a![]() -a
-a![]() )(1+a-
)(1+a-![]() a-
a-![]() ).
).
若0<a<1,则a2-1<0,a![]() >a
>a![]() ,∴f(x2)>f(x1).∴y=f(x)在R上为增函数;
,∴f(x2)>f(x1).∴y=f(x)在R上为增函数;
若a>1,则a2-1>0,a![]() <a
<a![]() .∴f(x2)>f(x1).∴y=f(x)在R上为增函数.
.∴f(x2)>f(x1).∴y=f(x)在R上为增函数.
综上,a>0,且a≠1时,y=f(x)是增函数.
当堂练习:
1.A
; 2. A ; 3. B ;4. D
;5. D ; 6. 0;7. ![]() ;8. [0,2];9. 1<a<2;10.
;8. [0,2];9. 1<a<2;10.
![]() ;
;
11.根据集合中元素的互异性,在第一个集合中,x≠0,第二个集合中,知道y≠0,∴第一个集合中的xy≠0,只有lg(xy)=0,可得xy=1①,∴x=y②或xy=y③.由①②联立,解得x=y=1或x=y=-1,若x=y=1,xy=1,违背集合中元素的互异性,若x=y=-1,则xy=x=1,从而两个集合中的元素相同.①③联立,解得x=y=1,不符合题意.∴x=-1,y=-1,符合集合相等的条件.因此,log8(x2+y2)=log82=![]() .
.
12.(1) 解:![]()
![]()
=![]() ,当
,当![]()
![]() 时,
时,![]() ,
,
而![]() ,所以当
,所以当![]() 时,y有最小值
时,y有最小值![]() ;当
;当![]() 时, y有最大值3. (2)由已知,得
时, y有最大值3. (2)由已知,得
![]()
![]() =
=![]()
13.由图象关于原点对称知它是奇函数,得f(x)+f(-x)=0,即![]() ,
,
得![]() m= -1; (2)由(1)得
m= -1; (2)由(1)得![]() ,定义域是
,定义域是![]() ,
,
设![]() ,得
,得![]() ,所以当a>1时,f(x)
在
,所以当a>1时,f(x)
在![]() 上单调递减;当0<a<1时,f(x) 在
上单调递减;当0<a<1时,f(x) 在![]() 上单调递增.
上单调递增.
14.(1)由y=x2-1(x≥1),得y≥0,且x=![]() ,∴f-1(x)=
,∴f-1(x)=![]() (x≥0),
(x≥0),
即C2:g(x)= ![]() ,M={xx≥0}.
,M={xx≥0}.
(2)对任意的x1,x2∈M,且x1≠x2,则有x1-x2≠0,x1≥0,x2≥0.
∴g(x1)-g(x2)=![]() -
-![]() =
=![]() <
<![]() x1-x2.
x1-x2.
∴y=g(x)为利普希茨Ⅰ类函数,其中a=![]() .
.
§2.4幂函数
经典例题:解:(1)∵所给的三个数之中1.5![]() 和1.7
和1.7![]() 的指数相同,且1的任何次幂都是1,因此,比较幂1.5
的指数相同,且1的任何次幂都是1,因此,比较幂1.5![]() 、1.7
、1.7![]() 、1的大小就是比较1.5
、1的大小就是比较1.5![]() 、1.7
、1.7![]() 、1
、1![]() 的大小,也就是比较函数y=x
的大小,也就是比较函数y=x![]() 中,当自变量分别取1.5、1.7和1时对应函数值的大小关系,因为自变量的值的大小关系容易确定,只需确定函数y=x
中,当自变量分别取1.5、1.7和1时对应函数值的大小关系,因为自变量的值的大小关系容易确定,只需确定函数y=x![]() 的单调性即可,又函数y=x
的单调性即可,又函数y=x![]() 在(0,+∞)上单调递增,且1.7>1.5>1,所以1.7
在(0,+∞)上单调递增,且1.7>1.5>1,所以1.7![]() >1.5
>1.5![]() >1.
>1.
(2)(-![]() )
)![]() =(
=(![]() )
)![]() ,(-
,(-![]() )
)![]() =(
=(![]() )
)![]() ,1.1
,1.1![]() =[(1.1)2]
=[(1.1)2]![]() =1.21
=1.21![]() .
.
∵幂函数y=x![]() 在(0,+∞)上单调递减,且
在(0,+∞)上单调递减,且![]() <
<![]() <1.21,
<1.21,
∴(![]() )
)![]() >(
>(![]() )
)![]() >1.21
>1.21![]() ,即(-
,即(-![]() )
)![]() >(-
>(-![]() )
)![]() >1.1
>1.1![]() .
.
(3)利用幂函数和指数函数的单调性可以发现0<3.8![]() <1,3.9
<1,3.9![]() >1,(-1.8)
>1,(-1.8)![]() <0,从而可以比较出它们的大小.
<0,从而可以比较出它们的大小.
(4)它们的底和指数也都不同,而且都大于1,我们插入一个中间数31.5,利用幂函数和指数函数的单调性可以发现31.4<31.5<51.5.
当堂练习:
1.B
; 2. B ; 3. B ;4. C
;5. B ; 6. ![]() ,
,![]() ;7.
;7. ![]() ;8. (-∞, 0);
;8. (-∞, 0);
9. (-∞, 1);10. (0,+∞);
11.因![]() ,
,![]() ,所以
,所以![]()
12. 函数y=x![]() 的定义域是R;值域是(0, +∞);奇偶性是偶函数;
在(-∞, 0)上递减;在[0,
+∞ )上递增.
的定义域是R;值域是(0, +∞);奇偶性是偶函数;
在(-∞, 0)上递减;在[0,
+∞ )上递增.
13.(1)设f (x)=xa, 将x=3, y=![]() 代入,得a=
代入,得a=![]() ,
, ![]() ;
;
设g(x)=xb, 将x=-8, y=-2代入,得b=![]() ,
,![]() ;
;
(2)f (x)既不是奇函数,也不是偶函数;g(x)是奇函数;(3) (0,1).
14.这是复合函数问题,利用换元法令t=15-2x-x2,则y=![]() ,
,
(1)由15-2x-x2≥0得函数的定义域为[-5,3],
∴t=16-(x-1)2![]() [0,16].∴函数的值域为[0,2].
[0,16].∴函数的值域为[0,2].
(2)∵函数的定义域为[-5,3]且关于原点不对称,∴函数既不是奇函数也不是偶函数.
(3)∵函数的定义域为[-5,3],对称轴为x=1,
∴x![]() [-5,1]时,t随x的增大而增大;x
[-5,1]时,t随x的增大而增大;x![]() (1,3)时,t随x的增大而减小.
(1,3)时,t随x的增大而减小.
又∵函数y=![]() 在t
在t![]() [0,16]时,y随t的增大而增大,
[0,16]时,y随t的增大而增大,
∴函数y=![]() 的单调增区间为[-5,1],单调减区间为(1,3).
的单调增区间为[-5,1],单调减区间为(1,3).
基本初等函数Ⅰ单元测试
1.B;
2.B; 3.D; 4.C; 5.D; 6.D; 7.B; 8.D; 9.A; 10.B; 11. ![]() ;12.1; 13.
;12.1; 13.![]() ;14.
;14.![]() ;
;
15.(-∞, 0); 16.(1)设![]() ,则
,则![]() ,
,![]() ,得
,得![]() ;
;
(2)原式=![]() . 17.依题意,有 lg[(100x-10x+1)2+1]=lg(242+1),
. 17.依题意,有 lg[(100x-10x+1)2+1]=lg(242+1),
∴(100x-10x+1)2+1=242+1, ∴100x-10x+1=24或100x-10x+1=-24, 解得10x=4或10x=6或10x==12或10x=-2(舍) ∴ x=lg4或x=lg6或x=lg12.
18.若![]() ,则由
,则由![]() 是单调递增的,与题设矛盾; 同理若
是单调递增的,与题设矛盾; 同理若![]() 时与题设矛盾;所以必有a<1,c>1从而
时与题设矛盾;所以必有a<1,c>1从而![]() -lga>lgc,得lg(ac)<0,
-lga>lgc,得lg(ac)<0,![]() .
.
19.(1)它是偶函数; (2) 函数f (x)在x∈[0, +∞]上是单调递增函数;
(3)
2y=ex+e-x, ∴e2x-2yex+1=0, 解得ex=y+![]() , ∴
, ∴ ![]() , x≥1.
, x≥1.
20.(1)由![]() ,∴
,∴ ![]() ,
,![]() .∴ x>0, ∴ 定义域为(0,+∞).
.∴ x>0, ∴ 定义域为(0,+∞).
(2)设![]() ,a>1>b>0,∴
,a>1>b>0,∴ ![]()
![]()
![]()
∴ ![]() ∴
∴ ![]() .∴
.∴ ![]() .
.
∴ ![]() 在(0,+∞)是增函数.
在(0,+∞)是增函数.
(3)当![]() ,+∞
,+∞![]() 时,
时,![]() ,要使
,要使![]() ,须
,须![]() , ∴ a-b≥1.
, ∴ a-b≥1.
§2.5函数与方程
经典例题:解:设y=x2-2x-3和y=a,利用Excel、图形计算器或其他画图软件,分别作出这两个函数的图象,它们的交点的个数,即为所给方程实根的个数.如下图,当a=0或a>4时,有两个实根;当a=4时,有三个实根;当0<a<4时,有四个实根.

当堂练习:
1.C
; 2. A ; 3. C ;4. C
;5. C ; 6.![]() ; 7.
; 7.![]() ; 8.a≤-4; 9. 4; 10. (2);
; 8.a≤-4; 9. 4; 10. (2);
11.设f(x)= mx2+2(m+3)x+2m+14,根据图象知当![]() 或
或![]() 时,符合题意
时,符合题意
从而得![]() .
.
12. (1)设抛物线与x轴相交于点(x1,0),(x2,0),则![]()
![]() ,
,
得![]() ;
;
(2) ![]() =
=![]() =
=![]()
13.(1)由![]() ,
,
![]() 即函数
即函数![]() 的图象交于不同两点A,B;
的图象交于不同两点A,B;
(2)![]() 知函数F(x)在[2,3]上为增函数,
知函数F(x)在[2,3]上为增函数,![]()
(3)设方程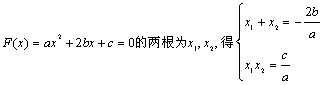
![]()
![]()
设![]() 的对称轴为
的对称轴为![]() 上是减函数
上是减函数![]()
14.解:原方程转化为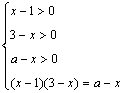 ,即方程x2-5x+a+3=0在区间(1,3)内是否有根,由
,即方程x2-5x+a+3=0在区间(1,3)内是否有根,由![]() 得:
得:![]() ,设f(x)= x2-5x+a+3,对称轴是
,设f(x)= x2-5x+a+3,对称轴是![]() ,若
,若![]() 得有一根在区间(1,3)内,即当
得有一根在区间(1,3)内,即当![]() 时,原方程有一根; 若
时,原方程有一根; 若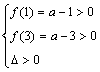 得
得![]() 时,原方程有两根;
时,原方程有两根;
![]() 时, 原方程无解.
时, 原方程无解.
§2.6函数模型及其应用
经典例题:解:设x年后我国人口总数为y,则有y=12·(1+0.0125)x,依题意,得y>14,
即12·(1+0.0125)x>14,即(1+0.0125)x>![]() .
.
两边取对数,得xlg1.0125>lg14-lg12.所以x>![]() ≈12.4.
≈12.4.
答:13年后,即2008年我国人口总数将超过14亿.
当堂练习:
1.A
; 2. C ; 3. D ;4. A
;5. C ; 6. 神州行; 7. y= -10x+560,31, 6250; 8. 2500; 9. 大于34; 10. 600![]() ;
;
11.
(1)依题得,
(2)设第二次服药时在第一次服药后t1小时,则![]() ,因而第二次服药应在11:00; 设第三次服药在第一次服药后t2小时,则此时血液中含药量应为两次服药量的和,即有
,因而第二次服药应在11:00; 设第三次服药在第一次服药后t2小时,则此时血液中含药量应为两次服药量的和,即有![]() 解得t2=9小时,故第三次服药应在16:00;设第四次服药在第一次后t3小时(t3>10),则此时第一次服进的药已吸收完,此时血液中含药量应为第二、三次的和,
解得t2=9小时,故第三次服药应在16:00;设第四次服药在第一次后t3小时(t3>10),则此时第一次服进的药已吸收完,此时血液中含药量应为第二、三次的和,![]() 解得t3=13.5小时,故第四次服药应在20:30.
解得t3=13.5小时,故第四次服药应在20:30.
12.设每日来回y次,每次挂x节车厢,由题意,y=kx+b,且当x=4时,y=16;当x=7时,y=10.解得:k=-2,b=24,∴y=-2x+24. 由题意,每次挂车厢最多时,营运人数最多,设每日拖挂W节车厢,则W=2xy=2x(-2x+24)=-4x2+48x=-4(x-6)2+144,
∴当x=6时,Wmax=144,此时,y=12,最多营运15840人.
13.解:依题意,价格上涨x%后,销售总金额为: y=a(1+x%)·
b(1-kx%)=![]() [-kx2+100(1-k)x+10000]. (1)取k=
[-kx2+100(1-k)x+10000]. (1)取k=![]() ,y=
,y=![]() [-
[-![]() x2+50x+10000],∴x = 50,
即商品价格上涨50%时, y最大为
x2+50x+10000],∴x = 50,
即商品价格上涨50%时, y最大为![]() ab. (2)因为y=
ab. (2)因为y=![]() [-kx2+100(1-k)x+10000],此二次函数开口向下,对称轴为x=
[-kx2+100(1-k)x+10000],此二次函数开口向下,对称轴为x=![]() ,在适当涨价过程中,销售总金额不断增加,即要求此函数当自变量x在{xx>0}的一个子集中增大时,y也增大.所以
,在适当涨价过程中,销售总金额不断增加,即要求此函数当自变量x在{xx>0}的一个子集中增大时,y也增大.所以![]() >0,解之0<k<1.
>0,解之0<k<1.
14.设二次函数为y=px2+qx+r,则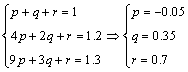 ,
,
所以![]() ,当x=4时,
y=1.3;
,当x=4时,
y=1.3;
对于函数![]() ,由
,由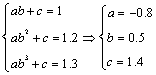 ,所以
,所以![]() ,当x=4时,
y=1.35,显然,用函数
,当x=4时,
y=1.35,显然,用函数![]() 作为模拟函数较好.
作为模拟函数较好.
函数的概念与基本初等函数Ⅰ章节测试
1.D;
2.D; 3.C; 4.C; 5.D; 6.C; 7.A; 8.D; 9.B; 10.D; 11. ![]() ; 12.3; 13. 0,2或-
; 12.3; 13. 0,2或-![]() ;
;
14. FB; 15.(-∞,-1)∪(1,+∞);
16.
![]()
![]()
![]() ,因xÎ[2,4], 函数的最小值为
,因xÎ[2,4], 函数的最小值为![]() ,所以0<a<1, 而函数的最大值为0,只有当x=2或4时取得,若x=2,由
,所以0<a<1, 而函数的最大值为0,只有当x=2或4时取得,若x=2,由![]() 得
得![]() ,解得
,解得![]() ,但
,但![]() 时,由
时,由![]() 得
得![]() ,舍去; 若x=4, 由
,舍去; 若x=4, 由![]() 得
得![]() ,解得
,解得![]() ,但
,但![]() 时,由
时,由![]() 得
得![]() ,舍去;综上所述,
,舍去;综上所述,![]() .
.
17.(1)因![]() ,得
,得![]() ,从而
,从而![]() ,
,![]()
![]() ; (2)记
; (2)记![]() ,得
,得![]() 在[1,2]上单调递减,故g(x)在区间[0,1] 上单调递减; (3)由(2)得g(x)min=g(1)=-3,g(x)max=g(0)=0, 值域是[-3,0].
在[1,2]上单调递减,故g(x)在区间[0,1] 上单调递减; (3)由(2)得g(x)min=g(1)=-3,g(x)max=g(0)=0, 值域是[-3,0].
18.(1)由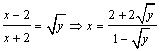 ,从而
,从而![]() ,其中
,其中![]() 且
且![]() ; 在
; 在![]() 和
和![]() 上分别单调递增;
上分别单调递增;
(2)![]() ,设
,设![]() 在
在![]() 上单调递增,所以g(x)min=g(0)=3.5.
上单调递增,所以g(x)min=g(0)=3.5.
19.(1)P=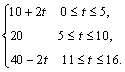 (Ⅱ)P-Q=
(Ⅱ)P-Q=
t=5时,Lmax=9![]() ,即第5周每件销售利润最大.
,即第5周每件销售利润最大.
20.(1)由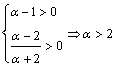 ; (2)由
; (2)由![]() 得
得![]() ,而logaa(β—1)<logaa(α—1),所以0<a<1,又由
,而logaa(β—1)<logaa(α—1),所以0<a<1,又由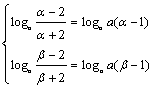 得α,β是方程
得α,β是方程![]() 的两根,整理得ax2+(a-1)x-2a+2=0,这方程有两个大于2的不相等的实根,
的两根,整理得ax2+(a-1)x-2a+2=0,这方程有两个大于2的不相等的实根,
得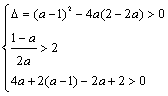 得
得![]() .
.
必修一综合测试
1.D;
2.A; 3.D; 4.C; 5.C; 6.B; 7.C; 8.C; 9.B; 10.B; 11.2; 12. 1或3; 13. 3,3; 14. ![]() ; 15.
; 15. ![]() ;
;
16.
![]()
![]()
![]()
![]()
又![]()
![]()
![]()
![]()
![]() 当
当![]() ,即
,即![]() 时,
时,![]() 取最大值,
取最大值,![]() .
.
![]() 当
当![]() ,即
,即![]() 时,
时,![]() 取最小值,
取最小值,![]() .
.
17. (1)由![]() 知
知![]() 必有实数根.
必有实数根.
或由![]() 得
得![]() 必有实数根.
必有实数根.
(2)当![]() 时,因为
时,因为![]() ,
,![]() ,
,
![]() ,
,
所以方程![]() 在区间
在区间![]() 上各有一个实数根.
上各有一个实数根.
18. (1)函数![]() 为R上的增函数.证明如下:
为R上的增函数.证明如下:
函数![]() 的定义域为R,对任意
的定义域为R,对任意
![]() ,
,![]()
![]() .
.
因为![]() 是R上的增函数,
是R上的增函数,![]() ,所以
,所以![]() <0,
<0,
所以![]() <0即
<0即![]() ,函数
,函数![]() 为R上的增函数.
为R上的增函数.
(2)存在实数a=1,使函数![]() 为奇函数.
为奇函数.
证明如下:当a=1时,![]() =
=![]() .
.
对任意![]() ,
,![]()
![]() =
=![]() =-
=-![]() =-
=-![]() ,即
,即![]() 为奇函数.
为奇函数.
19. (1)过点B作BD![]() AX,D为垂足,由于AC=x,AB=50,BD=30所以AD=40,CD=40-x,
AX,D为垂足,由于AC=x,AB=50,BD=30所以AD=40,CD=40-x,
由勾股定理得![]() .根据题意得:
.根据题意得:![]() ,
,
即![]() (
(![]() ).
).
(2)因为![]() ,所以y
,所以y![]() ,当
,当![]() 时,
时,![]() .
.
答:当![]() =30km时,单位重量货物的总运费最小,最小值为1600
=30km时,单位重量货物的总运费最小,最小值为1600![]() 元.
元.
20.
(1)∵![]() ,∴
,∴![]() ,由已知定理得,
,由已知定理得,![]() 的图象关于点
的图象关于点![]() 成中心对称;
成中心对称;
(2)首先证明![]() 在
在![]() 上是增函数,为此只要证明
上是增函数,为此只要证明![]() 在
在![]() 上是增函数.
上是增函数.
设![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上是增函数.
上是增函数.
再由![]() 在
在![]() 上是增函数得,
上是增函数得,
当![]() 时,
时,![]() ,即
,即![]() ;
;
(3)∵构造过程可以无限进行下去,∴![]() 对任意
对任意![]() 恒成立,
恒成立,
∴方程![]() 无解,即方程
无解,即方程![]() 无解或有唯一解
无解或有唯一解![]() ,
,
∴![]() 或
或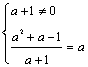 ,由此得到
,由此得到![]() .
.