3.2 简单的三角恒等变换
一、填空题
1.若![]() π<α<
π<α<![]() π,sin2α=-
π,sin2α=-![]() ,求tan
,求tan![]() ________________
________________
2.已知sinθ=-![]() ,3π<θ<
,3π<θ<![]() ,则tan
,则tan![]() 的值为___________.
的值为___________.
3.已知sin![]() +cos
+cos![]() =-
=-![]() ,且
,且![]() <α<3π,则cot
<α<3π,则cot![]() 的值为____________.
的值为____________.
4.已知α为钝角、β为锐角且sinα=![]() ,sinβ=
,sinβ=![]() ,则cos
,则cos![]() 的值为____________.
的值为____________.
5. 设5π<θ<6π,cos![]() =a,则sin
=a,则sin![]() 的值等于________________
的值等于________________
二、解答题
6.化简![]() .
.
7.求证:2sin(![]() -x)·sin(
-x)·sin(![]() +x)=cos2x.
+x)=cos2x.
8.求证:![]() .
.
9.在△ABC中,已知cosA=![]() ,求证:
,求证: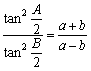 .
.
10. 求sin15°,cos15°,tan15°的值.
11. 设-3π<α<-![]() ,化简
,化简![]() .
.
12. 求证:1+2cos2θ-cos2θ=2.
13. 求证:4sinθ·cos2![]() =2sinθ+sin2θ.
=2sinθ+sin2θ.
14. 设25sin2x+sinx-24=0,x是第二象限角,求cos![]() 的值.
的值.
15. 已知sinα=![]() ,sin(α+β)=
,sin(α+β)=![]() ,α与β均为锐角,求cos
,α与β均为锐角,求cos![]() .
.
参考答案
一、填空题
1.
![]() . 2.-3 3.
. 2.-3 3. ![]() 4.
4.
![]() 5.-
5.-![]()
二、解答题
6.解:原式=![]()
=![]()
=![]()
=![]()
=tanθ.
7.证明:左边=2sin(![]() -x)·sin(
-x)·sin(![]() +x)
+x)
=2sin(![]() -x)·cos(
-x)·cos(![]() -x)
-x)
=sin(![]() -2x)
-2x)
=cos2x
=右边,原题得证.
8.证明:左边=![]()
=![]()
=![]()
=![]()
=![]()
=右边,原题得证.
9.证明:∵cosA=![]() ,
,
∴1-cosA=![]() ,
,
1+cosA=![]() .
.
∴![]() .
.
而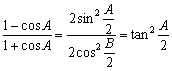 ,
,
![]() ,
,
∴tan2![]() ·tan2
·tan2![]() ,即
,即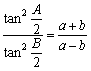 .
.
10.解:因为15°是第一象限的角,所以
sin15°= ,
,
cos15°= ,
,
tan15°=![]() =2-
=2-![]() .
.
11.解:∵-3π<α<-![]() ,∴-
,∴-![]() <
<![]() <-
<-![]() ,cos
,cos![]() <0.
<0.
又由诱导公式得cos(α-π)=-cosα,
∴![]() =-cos
=-cos![]() .
.
12.证明:左边=1+2cos2θ-cos2θ=1+2·![]() -cos2θ=2=右边.
-cos2θ=2=右边.
13.证明:左边=4sinθ·cos2![]() =2sinθ·2cos2
=2sinθ·2cos2![]() =2sinθ·(1+cosθ)
=2sinθ·(1+cosθ)
=2sinθ+2sinθcosθ=2sinθ+sin2θ=右边.
14.解:因为25sin2x+sinx-24=0,
所以sinx=![]() 或sinx=-1.
或sinx=-1.
又因为x是第二象限角,
所以sinx=![]() ,cosx=-
,cosx=-![]() .
.
又![]() 是第一或第三象限角,
是第一或第三象限角,
从而cos![]() =±
=± =±
=±![]() .
.
15.解:∵0<α<![]() ,∴cosα=
,∴cosα=![]() .
.
又∵0<α<![]() ,0<β<
,0<β<![]() ,
,
∴0<α+β<π.若0<α+β<![]() ,
,
∵sin(α+β)<sinα,∴α+β<α不可能.
故![]() <α+β<π.∴cos(α+β)=-
<α+β<π.∴cos(α+β)=-![]() .
.
∴cosβ=cos[(α+β)-α]
=cos(α+β)cosα+sin(α+β)sinα=-![]() ·
·![]() ·
·![]() ,
,
∵0<β<![]() ,
,
∴0<![]() <
<![]() .
.
故cos![]() .
.