2.3 平面向量的基本定理及坐标表示
一、选择题
1、平面直角坐标系中,O为坐标原点,已知两点A(3,1),B(-1,3),若点C满足![]() ,其中α、β∈R,且α+β=1,则点C的轨迹方程为 ( )
,其中α、β∈R,且α+β=1,则点C的轨迹方程为 ( )
A、3x+2y-11=0 B、(x-1)2+(y-2)2=5
C、2x-y=0 D、x+2y-5=0
2、若向量![]() =(x+3,x2-3x-4)与
=(x+3,x2-3x-4)与![]() 相等,已知A(1,2)和B(3,2),则x的值为
相等,已知A(1,2)和B(3,2),则x的值为
A、-1 B、-1或4 C、4 D、1或-4
3、已知平行四边形三个顶点的坐标分别为(-1,0),(3,0),(1,-5),则第四个顶点的坐标是( )
A、(1,5)或(5,5) B、(1,5)或(-3,-5)
C、(5,-5)或(-3,-5) D、(1,5)或(5,-5)或(-3,-5)
4、设i、j是平面直角坐标系内分别与x轴、y轴方向相同的两个单位向量,且![]() ,
, ![]() ,则△OAB的面积等于( )
,则△OAB的面积等于( )
A、15 B、10 C、7.5 D、5
5、己知P1(2,-1) 、P2(0,5)
且点P在P1P2的延长线上,![]() , 则P点坐标为( )
, 则P点坐标为( )
A、(-2,11) B、(![]() C、(
C、(![]() ,3) D、(2,-7)
,3) D、(2,-7)
6、一个平行四边形的三个顶点的坐标分别是(5,7),(-3,5),(3,4),则第四个顶点的坐标不可能是。 ( )
A、(-1,8) B,(-5,2) C、(1l,6) D、(5,2)
7、已知O为原点,A,B点的坐标分别为(a,0),(0,a),其中常数a>0,点P在线段AB上,且![]() =t
=t![]() (0≤t≤1),则
(0≤t≤1),则![]() ·
·![]() 的最大值为
( )
的最大值为
( )
A、a B、2a C、3a D、a2
8、已知![]() =(2,3) ,
=(2,3) , ![]() =(
=(![]() ,7) ,则
,7) ,则![]() 在
在![]() 上的投影值为( )
上的投影值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
二、填空题
9、已知点A(-1,5),若向量![]() 与向量
与向量![]() =(2,3)同向,且
=(2,3)同向,且![]() =3
=3![]() ,则点B的坐标为
,则点B的坐标为
10、平面上三个点,分别为A(2,-5),B(3,4),C(-1,-3),D为线段BC的中点,则向量![]() 的坐标为
的坐标为
三、解答题
11、已知O是坐标原点,点A在第一象限,![]() ,
,![]() ,求向量
,求向量![]() 的坐标、
的坐标、
12、已知点A(-1,2),B(2,8)及![]() ,
,![]() ,求点C、D和
,求点C、D和![]() 的坐标。
的坐标。
13、已知平行四边形ABCD的一个顶点坐标为A(-2,1),一组对边AB、CD的中点分别为M(3,0)、N(-1,-2),求平行四边形的各个顶点坐标。
14、已知点O(0,0),A(1,2),B(4,5)及![]() =
=![]() +t
+t![]() ,
,
求:(1)t为何值时,P在x轴上?P在y轴上?P在第二象限?
(2)四边形OABP能否构成平行四边形?若能,求出相应的t值;若不能,请说明理由。
15、已知向量![]() =(x,y)与向量
=(x,y)与向量![]() =(y,2y-x)的对应关系可用
=(y,2y-x)的对应关系可用![]() =f(
=f(![]() )表示。
)表示。
(1)证明:对于任意向量![]() 、
、![]() 及常数m、n,恒有f(m
及常数m、n,恒有f(m![]() +n
+n![]() )=mf(
)=mf(![]() )+nf(
)+nf(![]() )成立;
)成立;
(2)设![]() =(1,1),
=(1,1),![]() =(1,0),求向量f(
=(1,0),求向量f(![]() )及f(
)及f(![]() )的坐标;
)的坐标;
(3)求使f(![]() )=(3,5)成立的向量
)=(3,5)成立的向量![]() 。
。
参考答案
一、选择题
1、D;2、A;3、D;4、D;5、A;6、D;7、D;8、C
二、填空题
9、B(5,14)
10、![]() =
=![]()
三、解答题
11、解:设点A(x,y),则x=|![]() |
|![]() =
=![]()
![]() =
=![]() ,
,
y=|![]() |
|![]() =
=![]()
![]() =6,
=6,
即A(![]() ,6),所以
,6),所以![]() =(
=(![]() ,6)、
,6)、
12、解:设C(x1,y1),D(x2,y2),由题意可得![]() =(x1+1,y1-2),
=(x1+1,y1-2),![]() ,
,![]() =(-1-x2,2-y2),
=(-1-x2,2-y2),![]() =(-3,-6)
=(-3,-6)
∵![]() ,
,![]() ,∴(x1+1,y1-2)=
,∴(x1+1,y1-2)=![]() (3,6)=(1,2)
(3,6)=(1,2)
(-1-x2,2-y2)=-![]() (-3,-6)=(1,2),则有
(-3,-6)=(1,2),则有
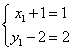 和
和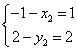 ,解得
,解得 和
和 、
、
∴C、D的坐标分别为(0,4)和(-2,0)、因此![]() =(-2,-4)、
=(-2,-4)、
13、解:设其余三个顶点的坐标为B(x1,y1),C(x2,y2),D(x3,y3)、
因为M是AB的中点,所以3=![]() ,0=
,0=![]() ,
,
解得x1=8,y1=-1、
设MN的中点![]() (x0,y0),则x0=
(x0,y0),则x0=![]() =1,y0=
=1,y0=![]() =-1,而
=-1,而![]() 既是AC的中点,又是BD的中点,
既是AC的中点,又是BD的中点,
所以x0=![]() ,y0=
,y0=![]() ,
,
即1=![]() ,-1=
,-1=![]() 、
、
解得x2=4,y2=-3、
同理解得x3=-6,y3=-1、
所以B(8,-1),C(4,-3),D(-6,-1)、
14、解:(1)![]() =
=![]() +t
+t![]() =(1+3t,2+3t)、
=(1+3t,2+3t)、
若P在x轴上,只需2+3t=0,所以t=-![]() 、
、
若P在y轴上,只需1+3t=0,所以t=-![]() 、
、
若P在第二象限,只需![]()
∴-![]() <t<-
<t<-![]() 、
、
(2)因为![]() =(1,2),
=(1,2),![]() =(3-3t,3-3t),若OABP为平行四边形,则
=(3-3t,3-3t),若OABP为平行四边形,则![]() =
=![]() 、
、
由于![]() ,无解,故四边形OABP不能构成平行四边形、
,无解,故四边形OABP不能构成平行四边形、
15、(1)证明:设向量![]() =(x1,y1),
=(x1,y1),![]() =(x2,y2),
=(x2,y2),
则f(mx1+nx2,my1+ny2)=(my1+ny2,2my1+2ny2-mx1-nx2)、
又mf(![]() )=(my1,2my1-mx1),nf(
)=(my1,2my1-mx1),nf(![]() )=(ny2,2ny2-nx2),
)=(ny2,2ny2-nx2),
所以mf(![]() )+nf(
)+nf(![]() )=(my1+ny2,2my1+2ny2-mx1-nx2)、
)=(my1+ny2,2my1+2ny2-mx1-nx2)、
所以f(m![]() +n
+n![]() )=mf(
)=mf(![]() )+nf(
)+nf(![]() )、
)、
(2)f(![]() )=(1,1),f(
)=(1,1),f(![]() )=(0,-1)、
)=(0,-1)、
(3)由![]() 得
得![]() 所以
所以![]() =(1,3)、
=(1,3)、