2.3 直线、平面垂直的判定及其性质
一、选择题
1、一条直线和平面所成角为θ，那么θ的取值范围是 （ ）
A、（0º，90º） B、[0º，90º] C、[0º，180º] D、[0º，180º)
2、两条平行直线在平面内的射影可能是①两条平行线；②两条相交直线；③一条直线；④两个点. 上述四个结论中，可能成立的个数是 （ ）
A、1个 B、2个 C、3个 D、4个
3、从平面外一点P引与平面相交的直线，使P点与交点的距离等于1，则满足条件的直线条数不可能是 （ ）
A、0条 B、1条 C、2条 D、无数条
4、已知平面a的斜线a与a内一直线b相交成θ角，且a与a相交成j1角，a在a上的射影c与b相交成j2角，则有 （ ）
A、coSθ=coSj1coSj2 B、coSj1=coSθcoSj2
C、Sinθ=Sinj1Sinj2 D、Sinj1=SinθSinj2
5、△ABC在平面
内，点P在外，PC⊥，且∠BPA=900，则∠BCA是 ( )
A、直角 B、锐角 C、钝角 D 、直角或锐角
6、正方体ABCD-A1B1C1D1中，与AD1垂直的平面是 ( )
A、平面DD1C1C B、平面A1DB1 C、平面A1B1C1D1 D、平面A1DB
7、菱形ABCD在平面内，PC⊥，则PA与BD的位置关系是
( )
A、平行 B、相交 C、垂直相交 D、异面垂直
8、与空间四边形四个顶点距离相等的平面共有 （ ）
A、四个 B、5个 C、6个 D、7个
二、填空题
9、设斜线与平面a所成角为θ，斜线长为l，则它在平面内的射影长是 .
10、一条与平面相交的线段，其长度为10cm，两端点到平面的距离分别是2cm，3cm，这条线段与平面a所成的角是 .
11、若10中的线段与平面不相交，两端点到平面的距离分别是2cm，3cm，则线段所在直线与平面a所成的角是 .
三、解答题
12、已知直线
平面，垂足为
，直线
，求证：
在平面内
13、已知一条直线
和一个平面平行，求证直线上各点到平面的距离相等
14、已知：a，b是两条异面直线，a^a，b^b，a∩b=，AB是a，b公垂线，交a于A，交b于B
求证：AB∥
15、如图，已知E，F分别是正方形ABCD边AD，AB的中点，EF交AC于M，GC垂直于ABCD所在平面．
（1）求证：EF⊥平面GMC．
（2）若AB＝4，GC＝2，求点B到平面EFG的距离．
参考答案
一、选择题
1、B；2、C；3、C；4、A；5、B；6、B；7、D；8、D
二、填空题
9、
10、
11、
三、解答题
12、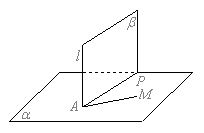
证明：设与确定的平面为
，
如果不在内，则可设
，
∵
，∴
，又∵，
于是在平面内过点有两条直线垂直于，
这与过一点有且只有一条直线一已知平面垂直矛盾，
所以一定在平面内
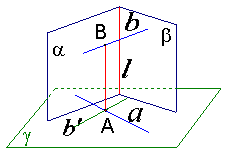
13、证明：过直线上任意两点A、B分别引平面的垂线
,垂足分别为
∵
∴
设经过直线的平面为，
∵// ∴ 
∴四边形
为平行四边形
∴
由A、B是直线上任意的两点，可知直线上各点到这个平面距离相等
14、证明方法一：（利用线面垂直的性质定理）
过A作
∥b，则a，可确定一平面γ
∵AB是异面垂线的公垂线，
即AB^a，AB^b
∴AB^
∴AB^γ
∵a^α，b^β，a∩b=
∴^a，^b ∴^
∴^γ ∴AB∥
证明方法二：（利用同一平面内垂直于同一直线的两条直线互相平行）
∵AB是异面直线a，b的公垂线，过AB与a作平面γ，γ∩a=m
∵a^a ∴a^m
又a^AB，ABÌγ
∴m∥AB
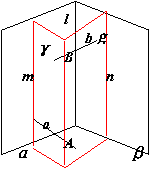又过AB作平面g，g∩β=n
同理：n∥AB
∴m∥n，于是有m∥β
又a∩b= ∴m∥
∴AB∥
15、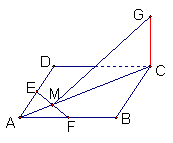
解：（1）连结BD交AC于O，
∵E，F是正方形ABCD边AD，AB的中点，AC⊥BD，
∴EF⊥AC．
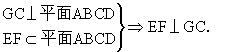
∵AC∩GC＝C，
∴EF⊥平面GMC．
（2）可证BD∥平面EFG，由例题2，正方形中心O到平面EFG
