2.2 直线、平面平行的判定及其性质
一、选择题
1、直线与平面平行的充要条件是 （ ）
A、直线与平面内的一条直线平行
B、直线与平面内的两条直线平行
C、直线与平面内的任意一条直线平行
D、直线与平面内的无数条直线平行
2、直线a∥平面a，点A∈a，则过点A且平行于直线a的直线 （ ）
A、只有一条，但不一定在平面a内
B、只有一条，且在平面a内
C、有无数条，但都不在平面a内
D、有无数条，且都在平面a内
3、若aËa，bËa，a∥a，条件甲是“a∥b”，条件乙是“b∥a”，则条件甲是条件乙的 （ ）
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分又不必要条件
4、A、B是直线l外的两点，过A、B且和l平行的平面的个数是 （ ）
A、0个 B、1个 C、无数个 D、以上都有可能
5、若
，则l与m的关系是
（ ）
A、
； B、l与m异面；C、
；D、
6、a,b是两条不相交的直线，则过直线b且平行于a的平面 （ ）
A、有且只有一个 B、至少有一个 C、至多有一个 D、只能有有限个
7、设AB,BC,CD是不在同一平面内的三条线段，则经过他们的中点的平面和直线AC的位置关系是 （ ）
A、平行 B、相交 C、平行或相交 D、AC在此平面内
二、判断题
8、过直线外一点只能引一条直线与这条直线平行. （ ）
9、过平面外一点只能引一条直线与这个平面平行. （ ）
三、填空题
10、在三棱锥的四个面中，直角三角形最多可能有________________个。
四、解答题
11、P是平行四边形ABCD外的一点，Q是PA的中点，求证：PC∥平面BDQ．
12、在正方体ABCD—A1B1C1D1中，AP＝B1Q，N是PQ的中点，M是正方形ABB1A1的 中心．求证：(1)MN∥平面B1D1；(2)MN∥A1C1．
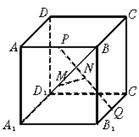
13、已知平行四边形ABCD与平行四边形ABEF共边AB，M、N分别在对角线AC、BF上，且AM∶AC＝FN∶FB． 求证：MN∥平面ADF．
14、已知平面
，BC∥，D∈BC，A
，直线AB、AD、AC分别交于E、F、G，且BC＝a，AD＝b，DF＝c，求EG的长度．
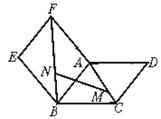
15、如图，□EFGH的四个顶点分别在空间四边形ABCD的边AB、BC、CD、DA上，求证：BD∥面EFGH，AC∥面EFGH．
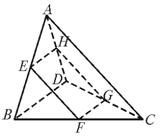
参考答案
一、选择题
1、D；2、B；3、A；4、D；5、D；6、B；7、A
二、判断题
8、正确
9、错误
三、填空题
10、4个
四、解答题
11、证明：如图，连结AC交BD于O
∵ ABCD是平行四边形，
∴ AO＝OC
连结OQ，则OQ
平面BDQ，
且OQ是△APC的中位线
∴ PC∥OQ，又PC在平面BDQ外
∴ PC∥平面BDQ．
12、证明：如图
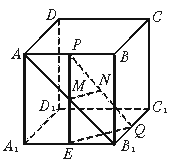
(1)连结PM交A1B1于E，连结AB1，则必过M．
在△APM和△B1EM中，
∠PAM＝∠EB1M
∠AMP＝∠B1ME
AM＝MB1
∴ △APM≌△B1EM
∴ AP＝EB1，PM＝ME，
即M为PE的中点，
又N为PQ的中点，
∴ MN∥EQ，而EQ面B1D1，
∴ MN∥平面B1D1．
(2)∵ EQ∥A1C1，MN∥EQ
由平行公理得MN∥A1C1．
13、证明：如图
作MP∥AB交AD于P，NQ∥AB交AF于Q，
则MP∥NQ，
由于
所以MP＝NQ，又已证MP∥NQ，
则MNQP是平行四边形，则MN∥PQ，
又因为MN不在平面ADF上，PQ在平面ADF内，
则MN∥平面ADF．
14、解：根据点A、线段BC和平面之间的不同位置关系，本题分三种情况
(1)如下图
∵ BC∥，BC平面ABC，平面ABC∩＝EF
∴ BC∥EF
∴ 
∴ 
，
即
，又
∴ EG＝
(2)如下图
∵ BC∥，BC平面ABC，平面ABC∩＝EF
∴ BC∥EF
∴ 
，∴ AF＝DF-DA＝c-b
∴ EG＝
(3)如下图
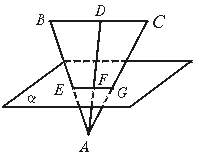
∵ BC∥，BC平面ABC，平面ABC∩＝EF
∴ BC∥EF
∴
∴ AF＝DA-DF＝b-c
∴ EG＝
15、证明：EFGH是平行四边形
BD∥面EFGH，
同理可证AC∥面EFGH．