函数、数列以及极限的综合题
例 已知函数
的图象是自原点出发的一条折线．当
时，该图象是斜率为
的线段（其中正常数
），设数列
由
定义． 求：
（1）求
和
的表达式；
（2）求
的表达式，并写出其定义域；
（3）证明：的图像与
的图象没有横坐标大于1的交点．
分析：本题主要考查函数的基本概念、等比数列、数列极限的基础知识，考查归纳、推理和综合的能力．
（1）由斜率分式求出，同样由斜率公式求出关于的递推式，然后求出，（2）由点斜式求出
段的的表达式，用极限的方法求出定义域．（3）与没有交点，只要
时
，或
时
恒成立，当，由于
，只要证
解：（1）依题意
，又由
，当
时，函数的图象是斜率为
的线段，故由
得
又由
，当
时，函数的图象是斜率为
的线段，故由
，即
得
记
由函数的图象中第
段线段的斜率为
，故得
又
∴
由此知数列
为等比数列，其首项为1，公比为
因，得
即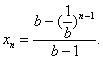
（2）当时，从（1）可知，即当
时，
当
时，即当
时，由（1）可知
为求函数的定义域，须对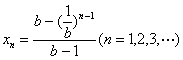
进行讨论．
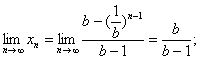
当时，
时，
，也趋向于无穷大．
综上，当时，的定义域为
当时，的定义域为
（3）证法1 首先证明当
时，恒有成立．
对任意的
，存在使
，此时有
又
即有成立．
其次，当
，仿上述证明，可知当
时，恒有成立．
故函数的图象与的图象没有横会标大于1的交点．
证法2 首先证明当
时，恒有成立．
用数学归纳法证明：
（ⅰ）由（1）知当
时，在
上，
所以
成立．
（ⅱ）假设
时在
上恒有成立．
可得
在
上，
所以 
也成立．
由（ⅰ）与（ⅱ）知，对所有自然数在
上都即
时，恒有
其次，当，仿上述证明，可知当
时，恒有成立．
说明： 本题不仅考查直线方程、数列、函数、不等式知识，还着重考查综合运用数学知识、思想方法解决问题的能力．解答本题首先必须具备较强的阅读理解能力，图象想像能力，本题的（2）用求极限的方法求定义域，反映了高考命题“不拘泥于大纲”的原则，不过从实践上看，与现在中学数学实际有些超前，本题的难度系数为0.02，三人平均不足1分，创了近年高考得分低的记录．
命题人设计试卷时为使考生不放弃难题，将本题放在倒数第二题的位置．本题得分低一方面是试题“超前”，另一方面反映考生能力差，现在中学数学备考主要是“大运用量”的模仿训练，创新精神提倡不够，一遇情境新颖的问题学生就毫无办法．以后坚持考不等式证明题的方向不会改变，试题难度会适度降低．
判断数列极限命题的真假
例 判断下列命题的真假：
（1）数列
的极限是0和1．
（2）数列
的极限是0．
（3）数列
的极限不存在．
（4）数列
的极限是0．
分析：判断一个数列否存在极限，极限是多少，主要依据极限的定义，即数列的变化趋势．
解：（1）一个数列的极限如果存在，它的极限是唯一的，不能是两个或更多个，是假命题．
（2）随着n无限增大，数列
的项无限趋近于0，因此它的极限是0，是真命题．
（3）随着n无限增大，数列
的项无限趋近于0，因此数列
无限趋近于0，是假命题．
（4）有穷数列无极限，是假命题．
说明：（3）中容易认为极限不存在．
（4）容易错误认为是真命题，尽管数列
随着n的增大而逐渐趋近于0，但由于数列只有10001项，是有穷数列，不存在极限．
根据数列的极限确定参数的范围
例 若
，则a的取值范围是（ ）
A．
B．
或
C．
D．
或
分析：由
（a为常数），知
，所以由已知可得
，解这个不等式就可求得a的取值范围．
解：由，得，
所以
，
两边平方，得：
，
，
所以或．
答案 B
说明：解题过程容易误认为只有
，得，错选A．解决含有涉及到求字母取值范围的问题时，常常要利用集合的包含关系，充要条件来考虑问题．
分析数列求极限
例 已知数列1.9，1.99，1.999，…，
，…．
（1）写出它的通项
；
（2）计算
；
（3）第几项以后所有的项与2的差的绝对值小于0.01？
（4）第几项以后所有的项与2的差的绝对值小于0.001？
（5）指出这个数列的极限．
分析：观察数列的特点，可以通过特殊数归纳总结规律，简化数列通项的一般形式，再求极限．
解：（1）可将数列改写为
（2-0.1），（2-0.01），（2-0.001），…，（
），…
于是此数列的通项
．
（2）
．
（3）令
即
，解得
故这个数列的第2项以后的所有项与2的差的绝对值均小于0.01．
（4）令
即
，解得
故这个数列的第3项以后的所有项与2的差的绝对值均小于0.001．
（5）
说明：可以通过特殊数帮助理解无限接近的意义，从而帮助求解极限．
求数列奇数项和的极限
例
数列
的前n项和记为
，已知
，求
的值．
分析：为求
当
的极限，应先求出的表达式．从已知条件中给出与的关系式，可以利用
，设法求出的表达式．
解：由
及
，可得
．
又
时，
，则
两式相减，得
于是，数列是以
为首项，公比为
的无穷等比数列．
进而可得，数列
是以为首项，公比为
的无穷等比数列，于是可求出极限．
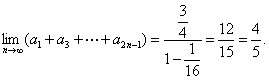
说明：这同1999年全国高考文史类试题．对于这类求极限的题目，必须先用数列的性质求出的通项公式，或确定数列的特征再求极限．由于所求数列是一个公式
的无穷等比数列，所以在解题时，可以不必再求极限，而直接代入无穷等比数列求和的公式
．
等比数列和的极限
已知数列
满足条件：
，
（
），且
是公比为q （
）的等比数列．设
（
），求
与
，其中
．
解：因为
，
所以
．
，所以
是首项为1+r ，公比为q的等比数列，从而
．
当
时，
，
；
当
时，
，
；
当
时，，
．
所以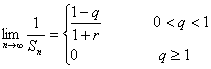
反思升华：
已知数列满足条件：，（），，对任意
，有
．设
，，求
．