分类讨论求极限
例 已知数列![]() 、
、![]() 都是由正数组成的等比数列,公比分别为
都是由正数组成的等比数列,公比分别为![]() ,其中
,其中![]() ,且
,且![]() ,
,![]() ,设
,设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,求
项和,求![]() .
.
(1997年全国高考试题,理科难度0.33)
解: ![]()
![]() .
.
分两种情况讨论;
(1)当![]() 时,∵
时,∵ ![]() ,故
,故![]() ,
,
∴![]()
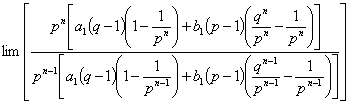
![]()
![]()
(2)当![]() 时,∵
时,∵ ![]() ,
,
∴ ![]()
![]()
![]()
![]() .
.
说明:该题综合考查了数列的基础知识、恒等变形的能力,分类讨论的数学思想方法和求极限的方法.
自变量趋向无穷时函数的极限
例 求下列极限:
(1)![]()
(2)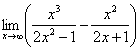
分析:第(1)题中,当![]() 时,分子、分母都趋于无穷大,属于“
时,分子、分母都趋于无穷大,属于“![]() ”型,变形的一般方法是分子、分母同除以x的最高次幂,再应用极限的运算法则.
”型,变形的一般方法是分子、分母同除以x的最高次幂,再应用极限的运算法则.
第(2)题中,当![]() 时,分式
时,分式![]() 与
与![]() 都趋向于∞,这种形式叫“∞-∞”型,变形的一般方法是先通分,变成“
都趋向于∞,这种形式叫“∞-∞”型,变形的一般方法是先通分,变成“![]() ”型或“
”型或“![]() ”型,再求极限.
”型,再求极限.
解:(1)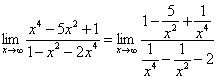
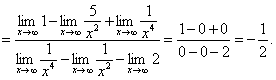
(2)
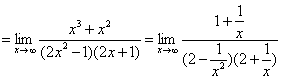
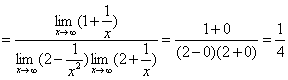
说明:“![]() ”型的式子求极限类似于数列极限的求法.
”型的式子求极限类似于数列极限的求法.
无穷减无穷型极限求解
例 求极限:
(1)![]()
(2)![]()
分析:含根式的函数求极限,一般要先进行变形,进行分子、分母有理化,再求极限.
解:(1)原式![]()
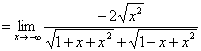
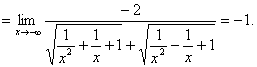
(2)原式![]()

说明:当![]() 时,
时,![]() ,因此
,因此 .
.
利用运算法则求极限
例 计算下列极限:
(1)![]() ;
;
(2)![]() .
.
(1992年全国高考试题,文科难度0.63)
解: (1)原式
 .
.
(2)原式
 .
.
说明:该题计算时,要先求和,再求所得代数式的极限,不能将只适用有限个数列的加、减、乘、除的数列极限的四则运算法则,照搬到无限个数列的加、减、乘、除,超出了法则的适用范围,下面的计算是错误的:
(1)原式![]()
(2)原式
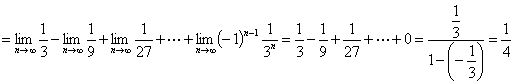
用二项式定理展开或逆用等比数列和公式化简求极限
例 设![]() ,求
,求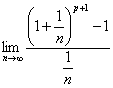 .
.
分析:把![]() 用二项式定理展开或逆用等比数列和公式即可求得.
用二项式定理展开或逆用等比数列和公式即可求得.
解:![]()

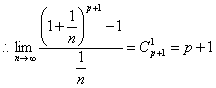
或:逆用等比数列求和公式:
原式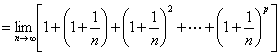
![]()
说明:要注意p是与n无关的正整数,![]() 不是无限项,对某些分式求极限应先对式子进行必要的变形,使之成为便于求极限的形式,以利问题的解决,经常用到的技巧是分母、分子有理化或按二项式定理展开等等.
不是无限项,对某些分式求极限应先对式子进行必要的变形,使之成为便于求极限的形式,以利问题的解决,经常用到的技巧是分母、分子有理化或按二项式定理展开等等.
零乘无穷型转化为无穷除无穷型
例 求![]()
分析:当![]() 时,所求极限相当于
时,所求极限相当于![]() 型,需要设法化为我们熟悉的
型,需要设法化为我们熟悉的![]() 型.
型.
解:
![]()
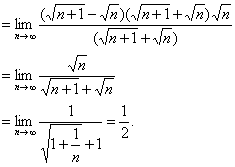
说明:对于这种含有根号的![]() 型的极限,可采取分子有理化或分母有理化来实现.如本题是通过分子有理化,从而化为
型的极限,可采取分子有理化或分母有理化来实现.如本题是通过分子有理化,从而化为![]() ,即为
,即为![]() 型,也可以将分子、分母同除以n的最高次幂即
型,也可以将分子、分母同除以n的最高次幂即![]() ,完成极限的计算.
,完成极限的计算.
根据极限确定字母的范围
例
已知![]() ,求实数m的取值范围.
,求实数m的取值范围.
分析:这是一个已知极限的值求参数的范围问题,我们仍然从求极限入手来解决.
解: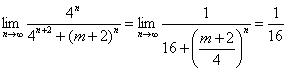
于是![]() ,即
,即![]() .
.
说明:在解题过程中,运用了逆向思维,由 可知,
可知,![]() 的极限必为0,而
的极限必为0,而![]() 的充要条件是
的充要条件是![]() ,于是解不等式
,于是解不等式![]() .
.
零比零型的极限
例 求![]() .
.
分析:这是一个![]() 型的极限,显然当
型的极限,显然当![]() 时,直接从函数
时,直接从函数![]() 分子、分母中约去x有困难,但是
分子、分母中约去x有困难,但是![]() 当
当![]() 时也趋近于0,此时x化为
时也趋近于0,此时x化为![]() ,这就启发我们通过换元来解决这一难题,即设
,这就启发我们通过换元来解决这一难题,即设![]() ,则
,则![]() .
.
解:设![]() ,则
,则![]() ,于是,当
,于是,当![]() 时,
时,![]() .
.
原式![]()
说明:本题采用的换元法是把![]() 化为
化为![]() ,这是一种变量代换.灵活地运用这种代换,可以解决一些
,这是一种变量代换.灵活地运用这种代换,可以解决一些![]() 型的极限问题.
型的极限问题.
例如对于![]() ,我们一般采用因式分解,然后约去
,我们一般采用因式分解,然后约去![]() ,得到
,得到![]() .其实也可以采用这种代换,即设
.其实也可以采用这种代换,即设![]() ,则当
,则当![]() 时,
时,![]() ,这样就有
,这样就有
![]()
组合与极限的综合题
例 ![]()
A.0 B.2 C.![]() D.
D.![]()
分析:将组合项展开后化简再求极限.
解: ![]()
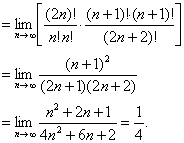
故应选D.
说明:本题考查组合的运算和数列极限的概念.
高考填空题
1.计算![]()
2.若数列![]() 的通项公式是
的通项公式是![]() ,则
,则![]()
3.计算:![]()
1.解析 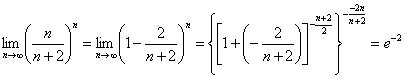
说明:利用数列极限公式![]() ,把原题的代数式稍加变形即可获解.本题主要考查灵活运用数列极限公式的能力.
,把原题的代数式稍加变形即可获解.本题主要考查灵活运用数列极限公式的能力.
2.解析 ![]()

说明:本题的思考障碍点是如何求![]() ?——只要懂得在通项公式中令
?——只要懂得在通项公式中令![]() ,可立得
,可立得![]() 的具体值,本题考查数列极限的基本知识.
的具体值,本题考查数列极限的基本知识.
3.解析 ![]()

说明:本题考查数列极限公式的应用.
根据已知极限和四则运算求其它极限
例 若![]() ,且
,且![]() 存在,则
存在,则![]()
A.0 B.![]() C.
C.![]() D.不存在
D.不存在
分析:根据题设知![]() 和
和![]() 均存在极限,这是进行极限运算的前提,然后相减即可求得结论.
均存在极限,这是进行极限运算的前提,然后相减即可求得结论.
解:![]()
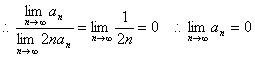
又![]()
∴![]()
即![]()
选C.
说明:![]() 是关键,不能错误地认为
是关键,不能错误地认为![]() ,
,![]() .
.
两个数列![]() 、
、![]() 的极限存在是两个数列的和.差、积存在极限的充分条件.但
的极限存在是两个数列的和.差、积存在极限的充分条件.但![]() 的极限不一定存在.
的极限不一定存在.
化简表达式再求数列的极限
例 求下列极限
(1)![]()
(2)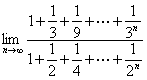
(3)![]()
分析:先运用等差数列、等比数列的前n项公式求和,或运用其他方式化简所给表达式,再进行极限的四则运算.
解:(1)原式![]()
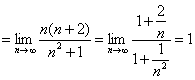
(2)原式
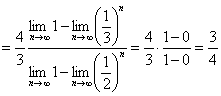
(3)原式![]()
说明:先化简,再求极限是求极限经常用到的方法,不能认为![]() 而得到(1)的结果是0.
而得到(1)的结果是0.
无穷比无穷和字母讨论的数列极限
例 求下列极限:
(1)![]() (2)
(2)![]()
分析:第(1)题属“![]() ”型,一般方法是分子,分母同除以各式中幂的值最大的式子.第(2)题中当a的值在不同范围内变化时,分子,分母的极限或变化趋势)不同,因此要分各种情形进行讨论.
”型,一般方法是分子,分母同除以各式中幂的值最大的式子.第(2)题中当a的值在不同范围内变化时,分子,分母的极限或变化趋势)不同,因此要分各种情形进行讨论.
解:(1)原式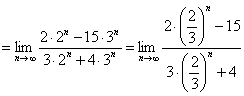

(2)当![]() 时,
时,![]() ,
,
当![]() 时,
时,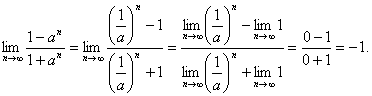
说明:含参数的式子求极限,经常要进行讨论,容易出现的问题是错误地认为![]() .
.
根据极限确定等比数列首项的取值范围
例 已知等比数列![]() 的首项为
的首项为![]() ,公比为q,且有
,公比为q,且有![]() ,求
,求![]() 的取值范围.
的取值范围.
分析:由已知条件及所给式子的极限存在,可知![]() 存在,因此可得q的取值范围,从而确定出
存在,因此可得q的取值范围,从而确定出![]() 的取值范围.
的取值范围.
解:由![]() ,得
,得![]() 存在.
存在.
∴![]() 且
且![]() 或
或![]() ..
..
当![]() 时,有
时,有![]() ,
,
∴![]() ,
,
∴![]() 解得
解得![]() ,
,
又![]() ,因此
,因此![]() .
.
当![]() 时,这时有
时,这时有![]() , ∴
, ∴![]() .
.
综上可得:![]() ,且
,且![]() 或
或![]() .
.
说明:在解决与数列有关的问题时,应充分注意相关知识的性质,仅从极限的角度出发来考虑q的特点,容易将![]() 这一条件忽视,从而导致错误.
这一条件忽视,从而导致错误.
求函数在某一点处的极限
例 求下列极限:
(1)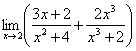
(2)![]()
(3)![]()
(4)![]()
分析:第(1)题中,![]() 在函数的定义域内,可直接用极限的四则运算法则求极限;(2)、(3)两个极限分子、分母都趋近于0,属“
在函数的定义域内,可直接用极限的四则运算法则求极限;(2)、(3)两个极限分子、分母都趋近于0,属“![]() ”型,必须先对函数变形,然后施行四则运算;(4)为“
”型,必须先对函数变形,然后施行四则运算;(4)为“![]() ”型,也应先对函数作适当的变形,再进行极限的运算.
”型,也应先对函数作适当的变形,再进行极限的运算.
解:(1)


![]()
(2)![]()
(3)![]()
![]()
(4)![]()
说明:不能错误地认为,由于![]() 不存在,
不存在,![]() 也不存在,因此(4)式的极限不存在.(4)属于“
也不存在,因此(4)式的极限不存在.(4)属于“![]() ”型,一般要先对函数式进行变形,变为“
”型,一般要先对函数式进行变形,变为“![]() ”型或“
”型或“![]() ”型,再求极限.
”型,再求极限.
函数在某一点处零比零型的极限
例 求下列极限:
(1)![]() (2)
(2)![]()
分析:第(1)题中,当![]() 时,分子、分母的极限都是0,不能用商的极限的运算法则,应该先对分式变形,约去一个极限为零的因式后再应用极限的运算法则求分式的极限,常用的变换方法有:
时,分子、分母的极限都是0,不能用商的极限的运算法则,应该先对分式变形,约去一个极限为零的因式后再应用极限的运算法则求分式的极限,常用的变换方法有:
①对多项式进行因式分解;②对无理式分子或分母有理化;③对三角函数式(如第(2)题,先进行三角恒等变换,再约分.
解:
(1)原式
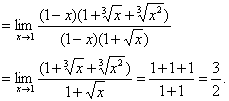
(2)原式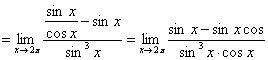
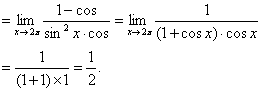
说明:如果分子、分母同乘以![]() ,对(1)式进行变形,思维就会受阻,正确的方法是分子、分母同乘以分子、分母的有理化因式,分母的有理化因式是
,对(1)式进行变形,思维就会受阻,正确的方法是分子、分母同乘以分子、分母的有理化因式,分母的有理化因式是![]() .
.