判断正误练习
判断下面说法是否正确,如果并说明原因。
(1)![]() 是纯虚数;
是纯虚数;
(2)在复平面内,原点也在虚轴上;
分析:先判断正误,若错误考虑如何纠错?或直接改正或举反例试之。
(1)错误。因为当![]() 时,不是纯虚数。
时,不是纯虚数。
(2)错误。因为原点不在虚轴上。
探究性问题
已知关于![]() 的方程
的方程![]() 有实根,求实数
有实根,求实数![]() 的取值。
的取值。
分析:注意不能用判别式△来解。
如:∵ 方程有实根
∴ ![]()
错误的原因是虚数不能比较大小,因此涉及到大小问题的概念和理论如与不等式有关的判别
解:设方程的实根为x0,则
![]()
整理得:![]()
由复数相等的条件知:

复数的分类例题
例
实数![]() 分别取什么值时,复数
分别取什么值时,复数![]() 是(1)实数(2)虚数(3)纯虚数。
是(1)实数(2)虚数(3)纯虚数。
解:实部![]() ,虚部
,虚部![]()
(1)当![]() 时,Z是实数;(2)当
时,Z是实数;(2)当![]() ,且
,且![]() 时,Z是虚数;(3)当
时,Z是虚数;(3)当![]() 或
或![]() 时是纯虚数.
时是纯虚数.
复数的相等例题
例
设![]() (
(![]() ),
),![]() ,当
,当![]() 取何值时,(1)
取何值时,(1)![]() ;(2)
;(2)![]()
分析:复数相等的充要条件,提供了将复数问题转化为实数问题的依据,这是解复数问题常用的思想方法,这个题就可利用复数相等的充要条件来列出关于实数![]() 的方程,求出
的方程,求出![]() 的值.
的值.
解:(1)由可得:
 解之得
解之得![]() ,
,
即:当![]() 时
时![]()
(2)当![]() 可得:
可得:
![]() 或
或![]() ,即
,即![]() 时
时![]()
复数与复平面上的点的对应关系的例题
例
设复数![]() 和复平面的点Z(
和复平面的点Z(![]() )对应,
)对应,![]() 、
、![]() 必须满足什么条件,才能使点Z位于:(1)实轴上?(2)虚轴上?(3)上半平面(含实轴)?(4)左半平面(不含虚轴及原点)?
必须满足什么条件,才能使点Z位于:(1)实轴上?(2)虚轴上?(3)上半平面(含实轴)?(4)左半平面(不含虚轴及原点)?
分析:本题主要考查复数![]() 与复平面的点Z(
与复平面的点Z(![]() )建立一一对应的关系.
)建立一一对应的关系.
解:(1)![]()
(2)![]() 且
且![]()
(3)![]()
(4)![]()
求点的轨迹的例题
例 已知关于t的一元二次方程![]()
(1)当方程有实根时,求点![]() 的轨迹方程.
的轨迹方程.
(2)求方程的实根的取值范围.
思路分析
(1)本题方程中有![]() 三个未知数由复数相等的充要条件能得到两个等式,而结论是要求动点
三个未知数由复数相等的充要条件能得到两个等式,而结论是要求动点![]() 的轨迹方程,联想到解析几何知识,求
的轨迹方程,联想到解析几何知识,求![]() 的轨迹方程就是求关于
的轨迹方程就是求关于![]() 的方程,于是上面的两个等式正是轨迹方程的参数形式,消去参数t,问题得解
的方程,于是上面的两个等式正是轨迹方程的参数形式,消去参数t,问题得解
(2)由上面解答过程中的②知![]() 可看作一条直线,由③知
可看作一条直线,由③知![]() 是一个圆,因此求实根t的范围可转化为直线与圆有公共点的问题.
是一个圆,因此求实根t的范围可转化为直线与圆有公共点的问题.
解答
(1)设实根为t,则![]()
即![]()
根据复数相等的充要条件得
由(2)得![]() 代入(1)得
代入(1)得![]()
即![]() ……(3)
……(3)
∴所求点的轨迹方程为![]() ,轨迹是以(1,-1)为圆心,
,轨迹是以(1,-1)为圆心,![]() 为半径的圆.
为半径的圆.
(2)由(3)得圆心为(1,-1),半径![]() ,
,
直线与圆有公共点,则![]() ,
,
即![]() ∴
∴![]() ,
,
故方程的实根的取值范围为![]() .
.
思维诊断
此题涉及到复数与解析几何的知识,综合性较强,学生往往不易入手,审题不到位,且有畏惧心理,是思维受阻的主要因素,在第(2)题求实根的取值范围时还可由(1)(2)消去y建立关于实数x的二次方程,用判别式![]() 求出t的范围.同时通过本题,同学们要进一步认识,把复数问题转化为实数问题求解的必要性,这是解决有关复数与方程问题惯用的手法,要切实掌握好.
求出t的范围.同时通过本题,同学们要进一步认识,把复数问题转化为实数问题求解的必要性,这是解决有关复数与方程问题惯用的手法,要切实掌握好.
复数相等的例题2
例 已知x是实数,y是纯虚数,且满足![]() ,求x与y.
,求x与y.
思路分析
因为y是纯虚数,所以可设![]() ,代入等式,把等式的左、右两边都整理成
,代入等式,把等式的左、右两边都整理成![]() 形式后,可利用复数相等的充要条件得到关于x与b的方程组,求解后得x与b值.
形式后,可利用复数相等的充要条件得到关于x与b的方程组,求解后得x与b值.
解答
设![]() 代入条件并整理得
代入条件并整理得
![]()
由复数相等的条件得![]() 解得
解得 ∴
∴![]()
思维诊断
一般根据复数相等的充要条件,可由一个复数等式得到两个实数等式组成的方程组,从而可确定两个独立参数,本题就是利用这一重要思想,化复数问题为实数问题得以解决.在解此题时,学生易忽视y是纯虚数这一条件,而直接得出等式![]() 进行求解,这是审题不细所致.
进行求解,这是审题不细所致.
复数相等的例题3
例 已知关于x的方程![]() 有实根,求这个实根以及实数k的值.
有实根,求这个实根以及实数k的值.
思路分析
方程的实根必然适合方程,设![]() 为方程的实根,代入整理后得
为方程的实根,代入整理后得![]() 的形式
的形式![]() .由复数相等的充要条件,可得关于
.由复数相等的充要条件,可得关于![]() 与k的方程组,通过解方程组便可求得
与k的方程组,通过解方程组便可求得![]() 与k.
与k.
解答
设![]() 是方程的实根,代入方程并整理得
是方程的实根,代入方程并整理得
![]()
由复数相等的条件得
解得 或
或
∴方程的实根为![]() 或
或![]() ,相应的k值为
,相应的k值为![]() 或
或![]() .
.
思维诊断
学生易给出如下错解:∵方程有实根,∴![]() .解得
.解得![]() 或
或![]() .这是由于错把实系数一元二次方程根的判别式运用到了复系数一元二次方程中,事实上,在复数集内解复系数一元二次方程,判别式
.这是由于错把实系数一元二次方程根的判别式运用到了复系数一元二次方程中,事实上,在复数集内解复系数一元二次方程,判别式![]() 不能够判断方程有无实根,这一点后面还会提到.因此,解关于方程有实根的问题,一般都是把实根代入方程,用复数相等条件求解.
不能够判断方程有无实根,这一点后面还会提到.因此,解关于方程有实根的问题,一般都是把实根代入方程,用复数相等条件求解.
复数的分类例题
例 m取何实数时,复数![]() (1)是实数?(2)是虚数?(3)是纯虚数?
(1)是实数?(2)是虚数?(3)是纯虚数?
思路分析
本题是判断复数在何种情况下为实数、虚数、纯虚数.由于所给复数z已写成标准形式,即![]() ,所以只需按题目要求,对实部和虚部分别进行处理,就极易解决此题.
,所以只需按题目要求,对实部和虚部分别进行处理,就极易解决此题.
解答
(1)当 即
即
∴![]() 时,z是实数.
时,z是实数.
(2)当 即
即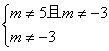
∴当![]() 且
且![]() 时,z是虚数.
时,z是虚数.
(3)当 即
即
∴当![]() 或
或![]() 时,z是纯虚数.
时,z是纯虚数.
思维诊断
研究一个复数在什么情况下是实数、虚数或纯虚数时,首先要保证这个复数的实部、虚部是有意义的,这是一个前提条件,学生易忽略这一点.如本题易忽略分母不能为0的条件,丢掉![]() ,导致解答出错.
,导致解答出错.