根据条件确定函数的参数是否存在
例
已知函数![]() ,是否存在实数a、b、c,使
,是否存在实数a、b、c,使![]() 同时满足下列三个条件:(1)定义域为R的奇函数;(2)在
同时满足下列三个条件:(1)定义域为R的奇函数;(2)在![]() 上是增函数;(3)最大值是1.若存在,求出a、b、c;若不存在,说明理由.
上是增函数;(3)最大值是1.若存在,求出a、b、c;若不存在,说明理由.
分析:本题是解决存在性的问题,首先假设三个参数a、b、c存在,然后用三个已给条件逐一确定a、b、c的值.
解:![]() 是奇函数
是奇函数![]()
又![]() ,即
,即![]() ,
,
∴![]() .
.
∴![]() 或
或![]() ,但
,但![]() 时,
时,![]() ,不合题意;故
,不合题意;故![]() .这时
.这时![]() 在
在![]() 上是增函数,且最大值是1.
上是增函数,且最大值是1.
设![]() 在
在![]() 上是增函数,且最大值是3.
上是增函数,且最大值是3.
![]() ,当
,当![]() 时
时![]() ,故
,故![]() ;又当
;又当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
故![]() ,又当
,又当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 是增函数,在(-1,1)上是减函数.
是增函数,在(-1,1)上是减函数.
又![]() 时,
时,![]() 时
时![]() 最大值为3.
最大值为3.
∴![]() 经验证:
经验证:![]() 时,
时,![]() 符合题设条件,所以存在满足条件的a、b、c,即
符合题设条件,所以存在满足条件的a、b、c,即![]()
说明:此题是综合性较强的存在性问题,对于拓宽思路,开阔视野很有指导意义.
此题若用相等方法解决是十分繁杂的,甚至无技可施.若用求导数的方法解决就迎刃而解.
因此用导数法解决有关单调性和最值问题是很重要的数学方法.切不可忘记.
供水站建在何处使水管费最少
例 有甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40km的B处,乙厂到河岸的垂足D与A相距50km,两厂要在此岸边合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元,问供水站C建在岸边何处才能使水管费用最省?
分析:根据题设条件作出图形,分析各已知条件之间的关系,借助图形的特征,合理选择这些条件间的联系方式,适当选定变元,构造相应的函数关系,通过求导的方法或其他方法求出函数的最小值,可确定点C的位置.
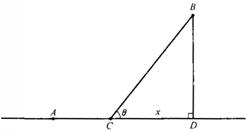
解:解法一:根据题意知,只有点C在线段AD上某一适当位置,才能使总运费最省,设C点距D点x km,则
![]() 又设总的水管费用为y元,依题意有
又设总的水管费用为y元,依题意有
![]()
![]() .令
.令![]() ,解得
,解得![]()
在(0,50)上,y只有一个极值点,根据实际问题的意义,
函数在![]() (km)处取得最小值,此时
(km)处取得最小值,此时![]() (km).
(km).
∴供水站建在A、D之间距甲厂20km处,可使水管费用最省.
解法二:设![]() ,则
,则![]()
∴![]() .
.
设总的水管费用为![]() ,依题意,有
,依题意,有
![]()
∴![]()
![]()
令![]() ,得
,得![]() .
.
根据问题的实际意义,当![]() 时,函数取得最小值,此时
时,函数取得最小值,此时![]() (km),即供水站建在A、D之间距甲厂20km处,可使水管费用最省.
(km),即供水站建在A、D之间距甲厂20km处,可使水管费用最省.
说明:解决实际应用问题关键在于建立数学模型和目标函数.把“问题情景”译为数学语言,找出问题的主要关系,并把问题的主要关系近似化、形式化,抽象成数学问题,再划归为常规问题,选择合适的数学方法求解.对于这类问题,学生往往忽视了数学语言和普通语言的理解与转换,从而造成了解决应用问题的最大思维障碍.
运算不过关,得不到正确的答案,对数学思想方法不理解或理解不透彻,则找不到正确的解题思路,在此正需要我们依据问题本身提供的信息,利用所谓的动态思维,去寻求有利于问题解决的变换途径和方法,并从中进行一番选择.
利用导数求函数的最值
例 求下列函数的最值:
1.![]() ;
;
2.![]() ;
;
3.![]()
4.![]() .
.
分析:函数![]() 在给定区间上连续可导,必有最大值和最小值,因此,在求闭区间
在给定区间上连续可导,必有最大值和最小值,因此,在求闭区间![]() 上函数的最值时,只需求出函数
上函数的最值时,只需求出函数![]() 在开区间
在开区间![]() 内的极值,然后与端点处函数值进行比较即可.
内的极值,然后与端点处函数值进行比较即可.
解:1.![]() ,令
,令![]() ,得
,得![]() ,
,
∴![]() .又
.又![]()
∴![]()
2.![]() ,令
,令![]() ,得
,得![]() ,
,
∴![]() ,
,
又![]() .
.
∴![]()
3.![]() .
.
令![]() ,即
,即![]() ,解得
,解得![]()
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
∴函数![]() 在点
在点![]() 处取得极小值,也是最小值为
处取得极小值,也是最小值为
![]() 即
即![]() .
.
4.函数定义域为![]() ,当
,当![]() 时,
时,
![]()
令![]() ,解得
,解得![]() ,∴
,∴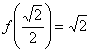 ,
,
又![]() ,∴
,∴![]()
说明:对于闭区间![]() 上的连续函数,如果在相应开区间
上的连续函数,如果在相应开区间![]() 内可导,求
内可导,求![]() 上最值可简化过程,即直接将极值点与端点的函数值比较,即可判定最大(或最小)的函数值,就是最大(或最小)值.解决这类问题,运算欠准确是普遍存在的一个突出问题,反映出运算能力上的差距.运算的准确要依靠运算方法的合理与简捷,需要有效的检验手段,只有全方位的“综合治理”才能在坚实的基础上形成运算能力,解决运算不准确的弊病.
上最值可简化过程,即直接将极值点与端点的函数值比较,即可判定最大(或最小)的函数值,就是最大(或最小)值.解决这类问题,运算欠准确是普遍存在的一个突出问题,反映出运算能力上的差距.运算的准确要依靠运算方法的合理与简捷,需要有效的检验手段,只有全方位的“综合治理”才能在坚实的基础上形成运算能力,解决运算不准确的弊病.
求两变量乘积的最大值
例 已知![]() 为正实数,且满足关系式
为正实数,且满足关系式![]() ,求
,求![]() 的最大值.
的最大值.
分析:题中有两个变量x和y,首先应选择一个主要变量,将![]() 表示为某一变量(x或y或其它变量)的函数关系,实现问题的转化,同时根据题设条件确定变量的取值范围,再利用导数(或均值不等式等)求函数的最大值.
表示为某一变量(x或y或其它变量)的函数关系,实现问题的转化,同时根据题设条件确定变量的取值范围,再利用导数(或均值不等式等)求函数的最大值.
解:解法一:![]() ,
,
∴![]() .
.
由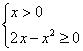 解得
解得![]() .
.
设![]()
当![]() 时,
时,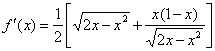
![]() .
.
令![]() ,得
,得![]() 或
或![]() (舍).
(舍).
∴![]() ,又
,又![]() ,∴函数
,∴函数![]() 的最大值为
的最大值为![]() .
.
即![]() 的最大值为
的最大值为![]() .
.
解法二:由![]() 得
得![]() ,
,
设![]() ,
,
∴![]() ,设
,设![]() ,
,
则![]()
![]()
令![]() ,得
,得![]() 或
或![]() .
.
![]() ,此时
,此时![]()
∴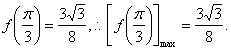
即当![]() 时,
时,![]()
说明:进行一题多解训练,是一种打开思路,激发思维,巩固基础,沟通联系的重要途径,但要明确解决问题的策略、指向和思考方法,需要抓住问题的本质,领悟真谛,巧施转化,方可快捷地与熟悉的问题接轨,在实现转化的过程中,关键是要注意变量的取值范围必须满足题设条件,以免解题陷于困境,功亏一篑.