利用导数求函数的极值
例 求下列函数的极值：
1．
；2．
；3．
分析：按照求极值的基本方法，首先从方程
求出在函数
定义域内所有可能的极值点，然后按照函数极值的定义判断在这些点处是否取得极值．
解：1．函数定义域为R．
令，得
．
当
或
时，
，
∴函数在
和
上是增函数；
当
时，
，
∴函数在（－2，2）上是减函数．
∴当
时，函数有极大值
，
当
时，函数有极小值
2．函数定义域为R．
令，得
或．
当
或时，，
∴函数在
和上是减函数；
当
时，，
∴函数在（0，2）上是增函数．
∴当时，函数取得极小值
，
当时，函数取得极大值
．
3．函数的定义域为R．
令，得
．
当
或
时，，
∴函数在
和
上是减函数；
当
时，，
∴函数在（－1，1）上是增函数．
∴当
时，函数取得极小值
，
当
时，函数取得极大值
说明：思维的周密性是解决问题的基础，在解题过程中，要全面、系统地考虑问题，注意各种条件 综合运用，方可实现解题的正确性．解答本题时应注意
只是函数在
处有极值的必要条件，如果再加之附近导数的符号相反，才能断定函数在处取得极值．反映在解题上，错误判断极值点或漏掉极值点是学生经常出现的失误．
复杂函数的极值
例 求下列函数的极值：
1．
；2．
分析：利用求导的方法，先确定可能取到极值的点，然后依据极值的定义判定．在函数的定义域内寻求可能取到极值的“可疑点”，除了确定其导数为零的点外，还必须确定函数定义域内所有不可导的点．这两类点就是函数在定义内可能取到极值的全部“可疑点”．
解：1．
令
，解得，但也可能是极值点．
当或时，，
∴函数在和上是增函数；
当时，，
∴函数在（0，2）上是减函数．
∴当时，函数取得极大值，
当时，函数取得极小值
．
2．
∴
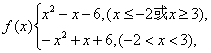
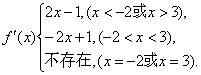
令，得
．
当或
时，，
∴函数在和
上是减函数；
当
或
时，，
∴函数在
和
上是增函数．
∴当和
时，函数有极小值0，
当时，函数有极大值
．
说明：在确定极值时，只讨论满足的点附近的导数的符号变化情况，确定极值是不全面的．在函数定义域内不可导的点处也可能存在极值．本题1中处，2中及处函数都不可导，但
在这些点处左右两侧异号，根据极值的判定方法，函数在这些点处仍取得极值．从定义分析，极值与可导无关．
根据函数的极值确定参数的值
例 已知
在时取得极值，且
．
1．试求常数a、b、c的值；
2．试判断是函数的极小值还是极大值，并说明理由．
分析：考察函数是实数域上的可导函数，可先求导确定可能的极值点，再通过极值点与导数的关系，即极值点必为的根建立起由极值点所确定的相关等式，运用待定系数法求出参数a、b、c的值．
解：1．解法一：
．
是函数的极值点，
∴
是方程，即
的两根，
由根与系数的关系，得
又，∴
， （3）
由（1）、（2）、（3）解得
．
解法二：由
得
， （1）
（2）
又，∴， （3）
解（1）、（2）、（3）得．
2．
，∴
当或时，，当时，
∴函数在和上是增函数，在（－1，1）上是减函数．
∴当时，函数取得极大值
，
当时，函数取得极小值．
说明：解题的成功要靠正确思路的选择．本题从逆向思维的角度出发，根据题设结构进行逆向联想，合理地实现了问题的转化，使抽象的问题具体化，在转化的过程中充分运用了已知条件确定了解题的大方向．可见出路在于“思想认识”．在求导之后，不会应用
的隐含条件，因而造成了解决问题的最大思维障碍．