导数定义的利用
例 若
，则
等于（ ）
A．
B．
C．
D．以上都不是
分析：本题考查的是对导数定义的理解，根据导数定义直接求解即可
解：由于
，应选A
求曲线方程的斜率和方程
例
已知曲线
上一点
，用斜率定义求：
（1）点A的切线的斜率
（2）点A处的切线方程
分析：求曲线在A处的斜率
，即求
解：（1）
（2）切线方程为
即
说明：上述求导方法也是用定义求运动物体
在时刻
处的瞬时速度的步骤．
判断分段函数的在段点处的导数
例 已知函数
，判断
在
处是否可导？
分析：对分段函数在“分界点”处的导数问题，要根据定义来判断是否可导．
解：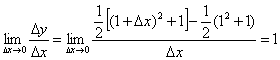
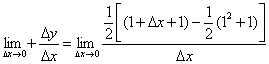
∴在处不可导．
说明：函数在某一点的导数，是指一个极限值，即
，当
；包括
；
，判定分段函数在“分界处”的导数是否存在时，要验证其左、右极限是否存在且相等，如果存在且相等，才能判定这点存在导数，否则不存在导数．
利用导数定义的求解
例 设函数在点
处可导，试求下列各极限的值．
1．
；
2．
3．若
，则
等于（ ）
A．－1 B．－2 C．－1 D．
分析：在导数的定义中，增量
的形式是多种多样的，但不论选择哪种形式，
也必须选择相对应的形式．利用函数在点处可导的条件，可以将已给定的极限式班等变形转化为导数定义的结构形式．
解：1．原式＝
2．原式＝
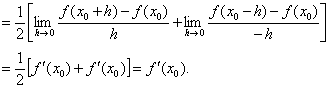
3．
（含
），
∴
故选A．
说明：概念是分析解决问题的重要依据，只有熟练掌握概念的本质属性，把握其内涵与外延，才能灵活地应用概念进行解题，不能准确分析和把握给定的极限式与导数的关系，盲目套用导数的定义是使思维受阻的主要原因．解决这类问题的关键就是等价变形，使问题转化．
利用定义求导数
例 1．求函数
在处的导数；
2．求函数
（a、b为常数）的导数．
分析：根据导数的概念求函数的导数是求导数的基本方法，确定函数
在
处的导数有两种方法，应用导数定义法和导函数的函数值法．
解：1．解法一（导数定义法）：
，
解法二（导函数的函数值法）：
，
∴
2．
说明：求导其本质是求极限，在求极限的过程中，力求使所求极限的结构形式转化为已知极限的形式，即导数的定义，这是能够顺利求导的关键，因此必须深刻理解导数的概念．
证明函数的在一点处连续
例
证明：若函数在点处可导，则函数在点处连续．
分析：从已知和要证明的问题中去寻求转化的方法和策略，要证明
在点处连续，必须证明
．由于函数在点处可导，因此，根据函数在点处可导的定义，逐步实现两个转化，一个是趋向的转化，另一个是形式（变为导数定义形式）的转化．
解：证法一：设
，则当
时，，
∴函数在点处连续．
证法二：∵函数在点处可导，
∴在点处有
∴
∴函数在点处连续．
说明：对于同一个问题，可以从不同角度去表述，关键是要透过现象看清问题的本质，正确运用转化思想来解决问题．函数在点处连续，有极限以及导数存在这三者之间的关系是：导数存在
连续有极限．反之则不一定成立．证题过程中不能合理实现转化，而直接理解为
是使论证推理出现失误的障碍．