高三理科数学综合测试试题(三)
1.已知命题p:![]() ,则 (C )
,则 (C )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.已知函数 ,则a的所有可能值组成的集合为B
,则a的所有可能值组成的集合为B
A.{1} B.![]() C.{-
C.{-![]() } D.{1,
} D.{1,![]() }
}
3.命题p:若![]() 的充分不必要条件;
的充分不必要条件;
命题q:函数![]() ,则 ( A )
,则 ( A )
A.“p\/q”为假 B.“![]() ”为真 C.p真q假 D.p假q真
”为真 C.p真q假 D.p假q真
4.不等式![]() 的解集是 ( A )
的解集是 ( A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.在等比数列{an}中,![]() ( C
)
( C
)
A.27 B.-27 C.![]() D.
D.![]()
6.给出下面类比推理命题(其中Q为有理数集,R为实数集,C为复数集):
①“若![]() ”类比推出“
”类比推出“![]() ”
”
②“若![]() ”类比推出
”类比推出
“
![]() ”
”
③“若![]() ”类比推出“若
”类比推出“若![]() ”
”
④“若![]() ”类比推出“若
”类比推出“若![]() ”
”
其中类比结论正确的个数有A.1 B.2 C.3 D.4 ( B )
7.在R上定义运算:![]() .若不等式
.若不等式![]() 对任意实数x恒成立,则 ( C )
对任意实数x恒成立,则 ( C )
A.![]() B.0<a<2 C.
B.0<a<2 C.![]() D.
D.![]()
8.设函数![]() ,则实数a的取值范围是 ( D )
,则实数a的取值范围是 ( D )
A.![]() B.(0,1) C.
B.(0,1) C.![]() D.
D.![]()
9.若复数z满足方程![]() ,则z=1-i
,则z=1-i
|
11.函数![]() 的单调递减区间是
的单调递减区间是![]()
12.若从集合P到集合Q={a,b,c}所有的不同映射共有81个,则从集合Q到集合P可作的不同映射共有64个.
13.已知![]() 的最小值为9
的最小值为9
∵![]() 当且仅当
当且仅当![]() 取等号
取等号
14.将正整数排成下表:
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
……
则数表中的300应出现在第18行.
(由已知可知所有的数字为公差为1的等差数列,每行的数字个数为以1为首项,2为公差的等差数列,前n行数字个数为n2.)
15.(本小题满分12分)在△ABC中,角A、B、C的对边分别为a、b、c.已知a+b=5,c=![]() ,且
,且![]()
(1)求角C的大小;
解:∵A+B+C=180°
由![]() …………1分
…………1分
∴![]() ………………3分
………………3分
整理,得![]() …………4分 解得:
…………4分 解得:![]() ……5分
……5分
∵![]() ∴C=60° ………………6分
∴C=60° ………………6分
(2)求△ABC的面积.
由余弦定理得:c2=a2+b2-2abcosC,即7=a2+b2-2ab …………7分
∴![]() …………8分 =25-3ab 9分
…………8分 =25-3ab 9分 ![]() 10分
10分
∴![]() …………12分
…………12分
17.(本小题满分14分)
在公差为d(d≠0)的等差数列{an}和公比为q的等比数列{bn}中,已知a1=b1=1,a2=b2,a8=b3.
(1)求数列{an}与{bn}的通项公式;(2)令![]() ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
解:(1)由条件得: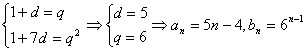 …………6分
…………6分
(2)![]()
![]() ①
①
![]() ②
②
①-②:![]()
即 ![]()
∴![]() …………14分
…………14分
16.(本小题满分12分)
某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(量大供应量)如下表所示:
|
消耗量 资源 | 甲产品(每吨) | 乙产品(每吨) | 资源限额(每天) |
| 煤(t) | 9 | 4 | 360 |
| 电力(kw·h) | 4 | 5 | 200 |
| 劳动力(个) | 3 | 10 | 300 |
| 利润(万元) | 6 | 12 |
问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?
解:设此工厂应分别生产甲、乙两种产品x吨、y吨.获得利润z万元 ……1分
 依题意可得约束条件:
依题意可得约束条件: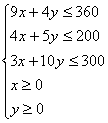 …………4分
…………4分
利润目标函数z=6x+12y …………8分
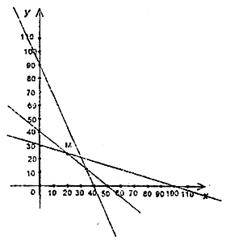
如图,作出可行域,作直线l:z=6x+12y,把直线l向右上方平移至l1位置,直线经过可行域上的点M,且与原点距离最大,此时z=6x+12y取最大值.
解方程组 ![]() ,得M(20,24) …………11分
,得M(20,24) …………11分
所以生产甲种产品20t,乙种产品24t,才能使此工厂获得最大利润 …………12分
18.(本小题满分14分)
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,AB=3米,AD=2米.
(Ⅰ)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
|
解:设AN的长为x米(x>2)
∵![]() ∴
∴![]()
∴![]() …………3分
…………3分
(Ⅰ)由SAMPN>32得![]() ,
,
∵![]()
∴![]() ,即AN长的取值范围是
,即AN长的取值范围是![]() …………6分
…………6分
(Ⅱ)令![]() …………9分
…………9分
∴当![]() 上单调递增,
上单调递增,
∴函数![]() 上也单调递增
…………11分
上也单调递增
…………11分
∴当x=6时,![]() 取得最小值即SAMPN取得最小值27(平方米)
取得最小值即SAMPN取得最小值27(平方米)
此时AN=6米,AM=4.5米 …………13分
答:当AM、AN的长度分别是4.5米,6米时,矩形AMPN的面积最小,最小面积是27平方米. ………………14分
19.(本小题满分14分)已知函数![]()
(Ⅰ)若![]() 上单调递增,求a的取值范围;
上单调递增,求a的取值范围;
解:(Ⅰ)由![]() …………2分
…………2分
欲使函数为![]() 上单调增函数,则
上单调增函数,则![]() 上恒成立,
上恒成立,
即不等式![]() 上恒成立,也即
上恒成立,也即 ![]() 上恒成立 4分
上恒成立 4分
令![]() ,上述问题等价于
,上述问题等价于![]() ,
,
而![]() 上的减函数,则
上的减函数,则![]() 为所求.6分
为所求.6分
(Ⅱ)若定义在区间D上的函数![]() 对于区间D上的任意两个值x1、x2总有以下不等式
对于区间D上的任意两个值x1、x2总有以下不等式![]() 成立,则称函数
成立,则称函数![]() 为区间D上的“凹函数”.试判断当
为区间D上的“凹函数”.试判断当![]() 是否为“凹函数”,并对你的判断加以证明
是否为“凹函数”,并对你的判断加以证明
证明:由![]() 得
得![]()
![]() …7分
…7分 ![]() …8分
…8分
而 ![]() ① …………10分
① …………10分
又![]() ② …………1分
② …………1分
∵![]() ∵
∵![]() ③ …13分
③ …13分
由①、②、③得 ![]()
即![]() ,从而由凹函数的定义可知函数为凹函数 …………14分
,从而由凹函数的定义可知函数为凹函数 …………14分
20.(本小题满分14分)
已知数列![]()
(1)计算x2,x3,x4的值;
(2)试比较xn与2的大小关系;
(3)设![]() ,Sn为数列{an}前n项和,求证:当
,Sn为数列{an}前n项和,求证:当![]() .
.
解:(1)![]() …………3分
…………3分
(2)∵当![]()
又![]()
∴![]()
以此类推有:![]() ………………8分
………………8分
(3)∵当![]() 时,
时,![]()
∴![]()
∴![]()
∴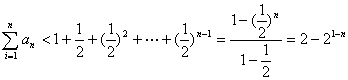 …………14分
…………14分
 产品
产品